导读:
邻近点算法(PPA)是求解非光滑优化问题的一种有效的迭代算法,对特殊结构问题的求解非常高效,但在实际问题中求解大规模可分离问题时花费很大。为解决上述问题且同时又保持PPA算法的优点,本文给出了一种非精确邻近梯度算法。该算法结合了线搜索法与邻近梯度下降算法的思想,在子问题的求解过程中采用近似的梯度,且不需要Lipschitz常数已知。基于以上思想,首先我们给出算法的伪代码,然后建立了算法收敛性的充分条件,最后证明在该条件下,算法迭代所产生序列的每个极限点是原问题的临界点。
01
基本信息:
一种非精确邻近梯度算法
An Inexact Proximal Gradient Algorithm
作者:
辜随佳, 王湘美:贵州大学数学与统计学院,贵州 贵阳
关键词:
邻近点算法;线搜索;收敛性分析;非精确梯度
项目基金:
国家自然科学基金(No. 12161017)
贵州省科技厅科技计划项目(No. ZK[2022]110)
原文链接:
https://doi.org/10.12677/pm.2024.145218
02
内容简介:
在汉斯出版社《理论数学》期刊上,有论文提出求解大规模复合凸优化问题的带线搜索的非精确邻近梯度算法,在算法的迭代过程中,对目标函数中的可分离部分采用非精确梯度,非精确邻近梯度算法不仅保留了邻近梯度算法易计算的优点,还在迭代过程中减小了数据储存量,提高了算法的效率。

由算法 1 可知,若在迭代过程的第 2 步采用全梯度,则算法 1 为精确的线搜索邻近梯度算法。下面的各类命题与定理中,都假设序列{xk}由算法 1 所产生。
命题 1 设 k ∈ N, βk 为算法 1 第 k 次迭代的 Step 3 中生成的步长,则对任意 x ∈ domh,有:

证明:对任意 x h ∈dom ,设

由(9)可得
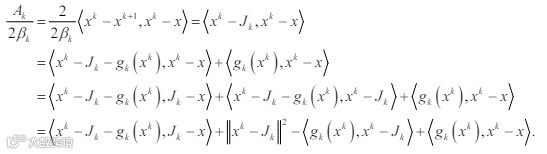
由(3)与(7)可得:
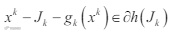
又 f 是光滑的凸函数,所以
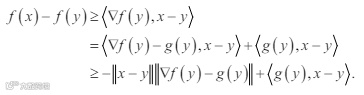
结合算法的第 3 步,并令 y= xk,得

于是

又由于
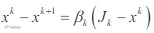
且 βk ∈(0,1) ,则 β2k ≤ βk 。即
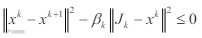
从而(10)得证。特别地,当 k x x = 时,由(10)有
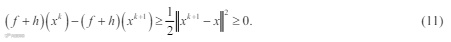
从而序列{(f+h)(xk)}单调减少,这说明算法 1 为下降算法。关于算法 1,有以下收敛性结论。
定理 1 设解集 S* ≠ ∅,{xk}和{βk} 为算法 1 所产生的序列。记d0 = dist(x0, S*) ,假设近似梯度 gk 连续且存在 a ≥1 满足

则序列{xk}收敛于 S* 中一点,即存在 x ∈ S*,使得

证明:在(7)中令 x = x* ∈ S*,有
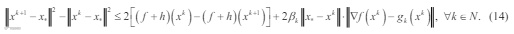
由于序列{(f+h)(xk)}单调递减,则

由(12)与引理 5 (用
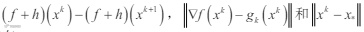
代替 ak,bk 和 ck )可知序列

有界,从而有
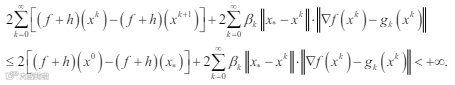
结合(14)与定义 3 可知序列{xk}quasi-Fejér 收敛到 S*。又由引理 4 知序列{xk}有界,假设 x 为{xk}的一个聚点,下面证明 x ∈ S*。令
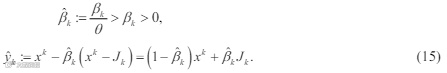
由算法 1 的 step3 可知

结合(2)和(15)可得
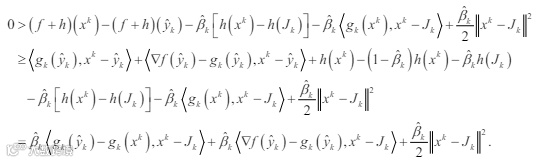
整理可得
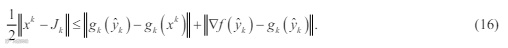
由于算子 proxh (⋅) 的非扩张性,由(7)可知

由(15)可知当 0 βk → 时,有
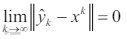
由 g 的连续性可知当 k → ∞ 时

结合引理 3 可知
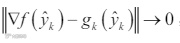
这表明了

注意 x 为{xk}的一个聚点,即存在子序列{xkj}收敛到 x ,则{Jk j} 也收敛到 x ,则又由引理 3 有

故在(3)中令 z = xkj-gkj(xkj)可得到
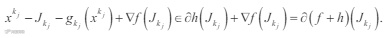
令 j → ∞ ,由(17)及(18)可得 0 ∈ ∂(f+h)(x) ,从而 x ∈ S*,由引理 4 可得(13)。
结论
本文介绍了一种求解大规模复合凸优化的非精确邻近梯度算法,算法不依赖可微函数的 Lipschitz 常数,并分析了算法的收敛性。接下来,我们可以构造求解大规模优化问题的非精确求解其他方法,得到高效的算法。
03
相关文章:
1.张金超. Stiefel流形上非光滑优化的一种带外推的可变度量邻近梯度算法[J]. 应用数学进展, 2022, 11(3): 1107-1115. https://doi.org/10.12677/AAM.2022.113119
2.童兴华, 彭定涛, 张弦. 一类混合稀疏组稀疏优化问题的邻近梯度算法[J]. 运筹与模糊学, 2023, 13(6): 7598-7611.
https://doi.org/10.12677/ORF.2023.136745
3.刘仁金, 王湘美. Hadamard流形上的多目标邻近梯度算法[J]. 理论数学, 2023, 13(12): 3525-3536.
https://doi.org/10.12677/PM.2023.1312367
4.刘海玉. 非凸优化中一种带非单调线搜索的惯性邻近算法[J]. 应用数学进展, 2021, 10(3): 732-739.
https://doi.org/10.12677/AAM.2021.103080
5.张景. 一类分式优化问题的带非单调线搜索的近端梯度次梯度算法研究[J]. 应用数学进展, 2024, 13(3): 1129-1139.
https://doi.org/10.12677/AAM.2024.133105
所属期刊


-Pure Mathematics-
《理论数学》是一本开放获取、关于理论数学领域最新进展的国际中文期刊,主要刊登理论数学领域最新研究进展的创造性论文和评论性文章。本刊支持思想创新、学术创新,倡导科学,繁荣学术,集学术性、思想性为一体,旨在给世界范围内的科学家、学者、科研人员提供一个传播、分享和讨论该领域内不同方向问题与发展的交流平台。

声明:本文转载仅仅是出于传播信息的需要,并不意味着代表本公众号观点或证实其内容的真实性;如其他媒体、网站或个人从本公众号转载使用,须保留本公众号注明的“来源”,并自负版权等法律责任。如本公众号内容不妥,或者有侵权之嫌,请先联系小编删除,万分感谢!
国外英语考试教学与研究|高中英语新教材练习系统对比研究——以人教版和译林版为例


投稿联系:027-86758873
QQ:2194278918
微信号:15802748706
投稿邮箱:2194278918@qq.com
合作联系:service@hanspub.org
点击“阅读原文”,免费下载论文



