主动脉瓣之“叶序”法则
——斐波那契序列美学
导语:一项来自意大利的Koshkelashvili教授及其同事对主动脉根部及主动脉瓣比例的原创研究发现:150例接受心电门控CT扫描患者的3D重建图像存在一个有趣的现象即主动脉窦高与瓣环的比例居然为1.69,几乎接近我们熟知的“黄金比例”,而这一数字广泛应用于大自然中。作为心脏外科医生,通过对正常三叶式主动脉瓣的几何形状进行观察,推测这种完美的“1.6比率”螺旋结构完全适合于主动脉瓣。这项研究分析了经食道超声下各种三叶主动脉瓣短轴视图,阐明了这种黄金比率在现代科学中的应用。
早在古希腊时代,人们就已经认识到0.618的神奇,并将其称为黄金分割率。而黄金分割率又是由斐波那契数列衍生而来。在人类发展史中,斐波那契数列作为数学界的重大发现,在数学理论和应用领域有着举足轻重的作用。除此之外,斐波那契数列还与自然界有着诸多联系,被人们称作“神奇数列”。
出于对这一数字的偏爱,它被应用到建筑和绘画等领域,从巴台农神庙到美国纽约众议院大楼,甚至基督十字架的分割比例也由它来定义,黄金分割率已经成为西方人追求外在美的内在规则。与此同时,人们也逐渐认识到黄金分割率广泛存在于自然界中,从花朵的图案中,棕榈树的叶子到肚脐对人体的分割几乎无处不在。

巴台农神庙

美国纽约众议院大楼
斐波那契数列是由意大利数学家列昂纳多·斐波那契(Leonardo Fibonacci)由“兔子繁殖问题”引出的数列,即 “如果一开始有一对兔子,它们每月生育一对兔子,小兔在出生后一个月又开始生育且繁殖情况与最初的那对兔子一样,那么一年后有多少对兔子?”,问题的答案并不复杂,但由此出现了一个有趣的现象:即每月底的家兔对数将做如下变化:1,1,2,3,5,8,13,21,34,55,89,144,233……该数列从第三项起每一项均是前两项之和,这就是著名的斐波那契数列,将数列中每相邻两项的前者除以后者,其极限结果就是黄金分割率-0.618。这个数列后来便以斐波那契的名字命名。
兔子繁殖法则

自然界的斐波那契序列
现代数学使用递归的方法将此数列总结为:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N)。经过仔细计算,我们可以发现前一项和后一项的比值越来越逼近黄金分割比例0.618。其实到了第9项,前一项和它的比值就已经非常非常接近于0.618。我们应该看过不少与黄金分割率相关的小故事,从人体、武器到建筑物,有很多符合人类美学观点或方便使用的设计都符合黄金分割率,人类认为它有严格的比例性、艺术性、和谐性。其实不但兔子的生育遵循着斐波那契数列的规律,自然界中也有不少动植物的生长遵循黄金分割率。比较有趣的一例就是叶片、花瓣及鳞片等的生长规律,即叶序(phyllotaxis)。有一位学者一片片的数过一朵重瓣芍药花的花瓣,最后得到的结果是233瓣,,233正好是斐波那契数列中的一项。还有一位中学生物教师,采得一棵松塔, 剥去鳞片数其片数,最后数得的鳞片数目是144片,这一结果仍在斐波那契数列内。植物学家在研究植物“叶序”(枝、叶及种子在植株上的排列与分布)时发现斐波那契数列仍起着重要的作用。这一数列的提出使我们对黄金分割的认识,从静态走向动态自然界的变化规律变得不再扑朔迷离了。
一些医生声称人体中特定的形状和结构可能遵从“黄金比例”,然而这个比率是否具有理性和科学性呢?还是说这只是一个偶然确定的数字吗?不同学者提出了不同的观点。Ashrafian等人发现冠状动脉分支系统和树的分支模式惊人相似,斐波那契系列可能代表了一种新的冠状动脉发育数学模型。Thuroff等人还假设主要冠状动脉分支的直径之和的比值接近“黄金比例”。Henein等人分析了健康患者和功能性二尖瓣反流的扩张型心肌病患者的二尖瓣环的比率(长度/宽度)分别为1.62和1.42,由此他们得出的结论是偏离了以“黄金比例”为代表的正常解剖结构有可能导致瓣环扭曲和扩大,从而导致二尖瓣反流。有趣的是心脏外科医生还观察到用于重塑的二尖瓣环(3D模拟)的长度/宽度也为1.62。

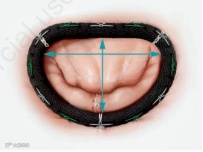
附图:用于心脏手术的人工二尖瓣环. 这种人工瓣环的长度/宽度之比为1.6,即所谓的“黄金比例”
虽然医生不太熟悉黄金比例,但是植物学家却很熟悉。“叶序”这个词来源于希腊语“叶和叶的排列”,从叶、花苞、树枝、花瓣、小花和鳞片几乎都遵从菲波那切数列规律。最早从公元前480年的古希腊绘画中就有证据,详细绘制了一颗有着“对生”的树,说明人类对叶状植物的兴趣在更早之前就开始了。在植物学界,叶序规律被认为是最引人注目的现象。

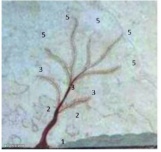
《潜水人之墓》(Tomb of the Diver),保存于那不勒斯国家考古博物馆,出土于古希腊墓的壁画。壁画描述了亡者正在去往地狱之门,也有说法说他生前曾是潜水员或喜欢跳水或潜水,在画的下方就绘制了一颗遵循斐波那契序列的“对生”的树。
叶序通常有三种-对生(opposite phyllotaxis)、轮生(whorled phyllotaxis)和互生(alternate phyllotaxis)。在对生叶序中,在茎枝的每个节上相对着生两片叶,如女贞、水杉和石竹等。对生叶序按照每一对叶子上下排列的方法又可分为两列对生(上、下对生叶的位置在茎的方向上一致,并保持对应生长)和交互对生(上、下对生叶错开一定的角度而展开,通常交叉排列呈直角)。轮生叶序则是在茎枝的每一个节上着生三片或三片以上的叶,如夹竹桃、百部和七叶一枝花。其中夹竹桃为三叶轮生,七叶一枝花为5~11叶轮生。目前在已经发现的植物中,出现最为频繁的叶序是互生叶序,而黄金分割率多数出现在互生叶序中,即茎的每节着生一片叶,除去常山型(orixate type)叶序中叶子以0、90、180、270的周期呈四列纵生,以及水青冈型(Fagus type)叶序呈特殊的二列纵生以外,多数情况随着茎的上升伸展成为斐波那契级数的互生,也就是螺旋状叶序的互生。
除此之外,葵花籽的排列、玫瑰花瓣的顺序、白菜叶的长法等皆如此。以双子叶植物的发芽过程为例,正常双子叶植物的子叶对生生长,此后第一对真叶以垂直于子叶的角度发出,接下来发生的叶片就不再垂直于第一对真叶的生长方向,而是偏离一定的角度,随着植物的生长这个角度慢慢地变得越来越接近137.5度[这实际上是2×(1-0.618)],即黄金分割角。从第一对真叶开始,叶片的发生同斐波那契数列的规律是一致的,因而从植物的正上方看叶片的发生,可以看到一个类似于斐波那契长方形所形成的螺旋,也就是“斐波那契螺旋”,它常存在于松果、贝壳、向日葵等植物中。

由斐波那契长方形所形成的斐波那契螺旋
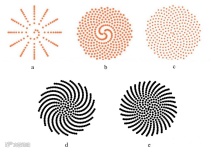
叶夹角分别为不同角度时呈现的叶序螺旋
(a:30°;b:124.34°;c:137.5°d:137.3°;e:137.6°)
大多数的植物都遵循“黄金比例”和“黄金分割角”序列理论,这被视为“适应性生存”,花瓣作为特化的叶片,和叶共享一套基因表达调控机制和激素调节机制,也是为了最大限度的暴露在阳光之下进行光合作用,还有减少挤压。这种叶序规律在人体上可以观察到,但是否适用于人体还不太清楚。
然后主动脉瓣就显示了一个极好的例子。
1510年,教会当局允许达·达芬奇进行尸体解剖,他深入研究了主动脉瓣和瓦式窦的解剖结构,在解剖研究文集的第115页中,他描述了正常三叶式主动脉瓣叶的完美对称性,以及确定了二叶以及四叶式主动脉瓣为异常变异。偏离正常解剖形状的异常变异可能导致湍流,最终导致瓣膜功能障碍。他解释了方形瓣膜(四叶式主动脉瓣)比正常三叶的孔径要大。然而,四叶主动脉瓣的每个小叶比正常三叶式的要小,以致它们对合时距离过远。


上图显示了主动脉瓣迷人的对称性,最终可以用六枚金色螺旋来表示,它们可以被切割成具有相同长宽比的正方形和小矩形。
从分子水平到多细胞形态水平,生物系统不可避免地表现出随机性。然而,也有些自然规律可以用数学术语来描述。“斐波那契序列”及其“黄金比率”被认为是一种数学规律性模型,它是叶序的基石之一,是植物学中研究植物如何分支的一部分。然而,我们目前还不知道这种数学模型是否可以适用于人类。不同的学者假设这种形状分割可能与人体(冠状动脉、心脏瓣膜等)中的“黄金比率”有关联。主动脉瓣和主动脉根部可能代表了一个有趣的人类分割几何模型,并且表明偏离正常的异构可能会导致功能障碍。然而,在缺乏科学验证的情况下,这样的研究只代表了作者对一个美丽形状的看法。
详细了解正常的主动脉瓣及根部的尺寸大小和标准比例是至关重要的,因为各种疾病都可以改变这些关系。当我们试图修复和置换这些瓣膜时,明白这些知识就显得尤为关键。基于这点,外科瓣膜置换或经导管主动脉瓣置换术时人工瓣膜就应该考虑到需模仿瓣膜原来理想化的正常比例。
Moscarelli, Ruggero De Paulis, The phyllotaxis of the aortic valve. Marco Monaldi Archives for Chest Disease ,2019, 89(3).



