图神经网络 (GNN) 是一种功能强大的机器学习模型,擅长分析以图形式表示的结构化数据,在社交网络分析和推荐系统等应用中表现出色。然而,经典的 GNN 在处理大规模图时面临可扩展性挑战。
2024年5月27日,Yidong Liao,Xiao-Ming Zhang与Chris Ferrie合作在arxiv期刊发表题为“Graph Neural Networks on Quantum Computers”(量子计算机上的图神经网络)的研究论文。

Yidong Liao 悉尼科技大学量子软件与信息中心

Xiao-Ming Zhang,北京大学量子计算与计算科学中心的博士后研究员(博雅博士后奖学金),与助理教授肖原一起合作。他于 2021 年获得香港城市大学博士学位。他的研究兴趣包括量子计算和量子控制。

Chris Ferrie 悉尼科技大学
本论文提出了在量子计算机上实现GNN的框架,以潜在解决这些挑战。论文作者设计了与三种基本类型的经典GNN相对应的量子算法:图卷积网络、图注意力网络和消息传递GNN。论文作者对简化图卷积(SGC)网络的量子实现进行了复杂度分析,显示出与经典对应物相比具有潜在的量子优势,在时间和空间复杂度上都有显著改进。复杂度可以在两者之间进行权衡:当优化以最小化电路深度时,量子SGC在输入大小上实现了对数时间复杂度(尽管以线性空间复杂度为代价)。当优化以最小化量子比特使用时,量子SGC显示出输入大小的对数空间复杂度,与经典SGC相比提供了指数级减少,同时仍保持更好的时间复杂度。这些结果表明论文作者的量子GNN框架能够有效处理大规模图。这项工作为在量子计算机上实现更先进的图神经网络模型铺平了道路,为分析图结构数据的量子机器学习开辟了新的可能性。

图神经网络(GNNs)是分析以图形式表示的结构化数据的强大工具。它们在多种应用中表现出显著的成功,包括社交网络分析和推荐系统。然而,在处理大规模图时,传统的GNNs遇到了可扩展性方面的挑战。这些挑战通常源于处理庞大且复杂的图结构时增加的内存需求和计算复杂性。因此,当处理在大数据分析和其他领域中常见的大型数据集时,GNNs的实际应用可能会受到限制。为了克服这些可扩展性问题,研究者们被激励去研究新的方法和技术,以扩展GNNs的能力,使它们在大规模图分析中更加高效和有效。
量子图神经网络(Quantum GNN)框架就是一种创新的方法,它利用量子计算的强大功能来处理和分析图结构数据。文章中提出的量子GNN框架是为了克服传统图神经网络在处理大规模图数据时遇到的可扩展性问题。这些框架具体包括:
(1)量子图卷积网络(Quantum Graph Convolutional Networks):这是一类模仿传统图卷积网络操作的量子算法,通过量子态的叠加和量子门操作来实现对节点特征的高效变换和聚合。
(2)量子图注意力网络(Quantum Graph Attention Networks):这种框架结合了注意力机制,允许模型在处理图数据时动态地聚焦于图中的特定部分,从而提高学习效率和预测精度。
(3)量子消息传递GNN(Quantum Message-Passing GNNs):该框架模拟了消息传递机制,通过量子信道在节点之间传递信息,以此来捕获节点间的复杂关系。
这些量子框架的提出,旨在利用量子计算的并行性和叠加性等特性,来提高图数据处理的速度和效率,从而在理论上解决传统GNNs在大规模图数据上的可扩展性问题。通过量子算法的实现,有望在图结构数据的分析和学习任务中取得突破性进展。
作者为三种基本类型的传统GNN设计了相应的量子算法,并提出了量子版本的简化图卷积(Simplified Graph Convolution, SGC)和线性图卷积(Linear Graph Convolution, LGC)。具体来说,量子版本的简化图卷积(Simplified Graph Convolution, SGC):SGC算法通过简化传统图卷积的操作来降低模型的复杂度,去除非线性激活函数,但仍然保持或甚至提高性能。作者为SGC设计了量子版本,利用量子计算的特性来进一步减少算法的时间和空间复杂度。而量子版本的线性图卷积(Linear Graph Convolution, LGC):LGC是SGC的一个更具有表现力的变体,它通过引入可学习的权重系数来对图的拉普拉斯矩阵的不同幂次进行加权求和,从而实现更丰富的图卷积滤波器。量子LGC算法利用量子奇异值变换(Quantum Singular Value Transformation, QSVT)来有效实现这种加权求和,进而优化算法性能。

图1. 三种量子GNN架构的总体电路构建以及三种“风格”的经典GNN层

图2. GNN 流程和三种“风格”的 GNN 层 :GNN 架构是排列等变的函数 F(X,A),通过在局部邻域上应用共享的排列不变函数 ϕ 来构建。这个局部函数 ϕ 有时被称为“扩散”、“传播”或“消息传递”,并且这样的 F 的整体计算被称为“GNN 层”。这些风格决定了ϕ 转换邻域特征的程度,允许在模拟图上交互时具有不同复杂性的水平。
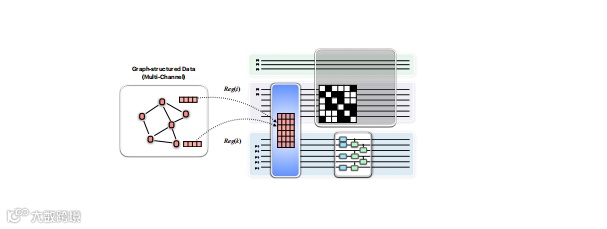
图3. 多通道GCN的线性逐层变换的量子实现。 多通道GCN的线性逐层变换(特定层的可训练权重矩阵和节点特征矩阵上的规范化邻接矩阵的乘法)可以通过在两个量子寄存器Reg(i)上应用规范化邻接矩阵的块编码和参数化量子电路来实现。

图4. 一个GNN层的完整量子电路示例(C=1,单通道)。 在我们的量子GCN中利用NTCA(非线性复振幅变换)来实现非线性激活函数,我们采用数据编码和图卷积的酉变换作为组成部分,构建一个新的酉变换,以生成期望状态,其振幅通过某些非线性函数进行变换。请注意,此图中的示意图仅用于说明目的。
这些量子算法的设计考虑了量子硬件的当前和未来能力,旨在通过量子优化来训练量子神经网络,并为量子计算机上的图结构数据分析铺平了道路。通过这些量子算法,可以在保持或提升GNN性能的同时,显著降低计算资源的需求,这对于大规模图数据的处理尤为重要。
其中,文章对量子SGC的实现进行了复杂性分析,展示了在时间和空间复杂性方面的潜在量子优势。量子SGC在最小化量子比特使用时,空间复杂性是对数级的,与经典SGC相比有指数级的减少;而在最小化电路深度时,时间复杂性也是对数级的。具体来说,在空间复杂性方面,当优化目标是最小化使用的量子比特数量时,量子SGC的空间复杂性呈现出对数级增长,这与传统的SGC算法相比,在空间需求上实现了指数级的降低。这一点对于量子硬件资源有限的情况尤为重要,因为它意味着量子SGC可以在保持较低资源消耗的同时处理更大规模的图数据。在时间复杂性方面,当优化目标是减少量子电路的深度时,量子SGC的时间复杂性同样展现出对数级增长。这表明量子SGC在执行图卷积操作时,相比于传统算法,能够在更少的计算步骤内完成,从而加快了处理速度。
文章中的这些分析结果表明,量子SGC算法在理论上能够在保持或提升性能的同时,显著减少资源消耗,这对于大规模图数据处理具有重要意义。量子算法的这些优势有望在未来量子计算技术成熟时得到实际应用,推动图神经网络在更广泛领域的应用发展。
未来,研究者计划进行更深入的分析和实证评估,以测试量子GNN架构在不同设置下的性能和可扩展性,特别是在现实世界的应用场景中。作者还会探索如何将传统GNN中更高级的架构和算法整合到量子计算领域,这可能包括将现有的成熟模型和策略适配到量子计算环境中;研究如何进一步优化量子GNN算法,以提高其效率和实用性,使其更适应量子硬件的特性和限制。
这些研究方向不仅有助于量子GNN架构的成熟和完善,也将推动量子计算技术在机器学习和人工智能领域的应用,为解决现实世界中的复杂问题提供新的工具和方法。
论文链接:https://arxiv.org/abs/2405.17060v1
江苏省海外人才创新创业联盟,是由江苏省科学技术协会主管的非法人非营利社会组织,简称苏创联。
2021年6月,苏创联由江苏省科协、世界绿色设计组织、欧盟中国城市发展委员会、中欧生命科学联盟、日本华侨华人博士协会、南京江北新区管委会、苏州工业园区管委会、南京江宁开发区管委会、江苏省绿色金融专业委员会等9家单位联合发起,秘书处设于中研绿色金融研究院,日常运营由科甄-中研在线团队负责。
联盟秘书处:
南京江北新区滨江大道396号3号楼4层
微信公众号:suchuanglian114
商务联系:
微信: w18701805508
邮箱: 18701805508 @139.com











