

【论文】哑铃型弹丸超高速正撞击防护板的数值仿真研究

数字仿真论坛

2018-10-12

导读：编者按：此文为第十四届中国CAE工程分析技术年会提交论文，收录于《第十四届中国CAE工程分析技术年会》论文集

编者按：此文为第十四届中国CAE工程分析技术年会提交论文，收录于《第十四届中国CAE工程分析技术年会》论文集中，著作权归作者所有。

徐峰，李德聪，吴国民

（中国舰船研究设计中心，湖北武汉，430064）

摘要：在地球周围的空间中，存在着大量的高速飞行的空间碎片，对航天器及人员的安全产生严重的威胁。通过开展哑铃型弹丸超高速正撞击Whipple防护板的数值仿真分析，用前板弹孔直径和后板毁伤面积来表征防护板的毁伤特性，得到了撞击速度、前板厚度、板间距等因素变化对防护板毁伤特性的影响规律；为防护板抗超高速撞击的防护设计提供一定的参考。研究表明：在相同条件下，随着撞击速度的增加，前板弹孔和后板毁伤直径增大；随着前板厚度的增加，前板弹孔直径增大，后板毁伤直径减小；随着板间距的增加，后板毁伤直径增大。

关键词：哑铃型弹丸、超高速、Whipple防护板

引言

随着航天事业的快速发展，空间碎片日益增多，严重威胁着人类的航天活动。多起由于空间碎片造成的航天器毁伤乃至灾难性事件，使得对航天器的空间防护问题得到了高度的重视^[1]。这些空间碎片与航天器的相互撞击速度约为6~7km/s量级，属超高速碰撞范畴^[²^]。现代航天器防护结构主要是基于1947年Whipple提出的Whipple防护结构发展起来的，其核心思想是：通过在舱壁外间隔一定距离设置防护板，当空间碎片超高速撞击防护板时，会将质量相对集中的碎片碎化为一定分布范围内质量微小碎片云，从而大大减轻对航天器的破坏^[3]。如“阿波罗”号宇宙飞船、“礼炮”号空间站、“天空实验室”空间站等的防护结构都是Whipple防护结构^[4]。对超高速撞击问题的研究方法主要有：（1）试验方法，通过多次地面超高速撞击实验，对碎片云的质量分布、构成以及速度分布以及后板损伤等进行了详细的研究，得到大量实验数据^[⁵^-⁷^]。（2）理论方法：主要是基于一维冲击波理论，建立描述碎片云的工程计算模型^[^8-9^]。（3）数值仿真方法：基于无网格的SPH方法开展超高速撞击的数值仿真计算，一方面与试验结果和理论进行对比，验证仿真方法的正确性；另一方面，获得撞击速度、弹丸直径、弹丸形状等对碎片云的影响规律，进行预报分析，用于指导航天器的防护设计^[1^0-11^]。在太空中，空间碎片是多种多样的，以球形最为常见，此外，还有圆盘形、椭球形、哑铃型、瓦片型、多面体型等。S.J.Hiermaier^[12]，Kuifeng Hu^[13]等人经过研究发现，基于球形弹丸的防护设计是不可靠的，形状的微小改变，对防护板的影响是很大的。为此，本文采用SPH方法开展哑铃型弹丸超高速正撞击铝合金whipple防护板进行数值仿真分析，获得撞击速度、前板厚度、板间距等因素变化对防护板毁伤特性的影响规律，为防护板抗超高速撞击的防护设计提供一定的参考。

1、计算模型及材料

1.1计算模型

图1为哑铃型弹丸超高速撞击Whipple防护结构示意图。Whipple防护板即为双层板结构，由前板、后板和两板间距组成。图2为哑铃型弹丸模型，弹丸特征尺寸A=1.4mm。哑铃型弹丸撞击速度为6.62km/s，前板厚度为0.8mm，规格为40mm×40mm，后板厚度为1mm，规格为60mm×60mm，板间距为30mm。弹丸、前板、后板材料均为铝合金Al2024-T4。

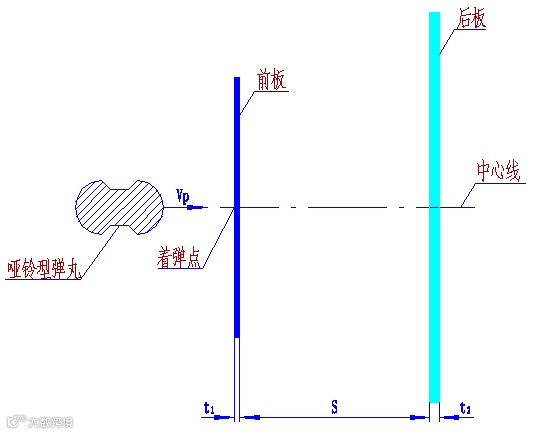
图1 Whipple防护结构示意图

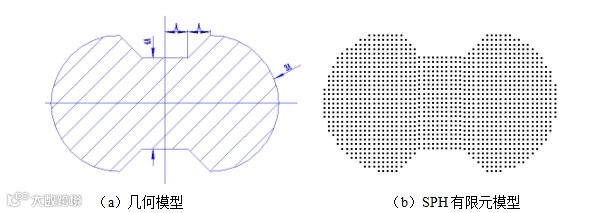
图2 哑铃型弹丸模型

为保证计算的精度和节省计算时间，SPH算法要求SPH粒子的初始空间分布应尽可能的规则而又均匀，所有粒子的质量应尽量接近，粒子间距也不应有太大的差异，否则时间步长急剧缩小而影响计算，无法达到计算要求^[¹⁴^]。因此，本文计算所用的弹丸、防护板的SPH有限元模型均通过自编FORTRAN程序生成。

1.2材料模型及状态方程

Johnson-Cook模型可以准确模拟金属材料在高应变率、大变形及高温条件下的强度行为，可以对冲击点远处及晚期的材料行为进行描述，具体表述如下：

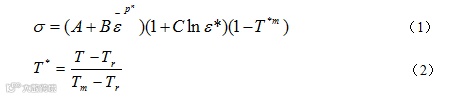
式中：为动态屈服应力；，是与材料相关的常数；为应变硬化影响系数；为应变率敏感系数；为温度软化系数；为等效塑性应变；为等效塑性应变率，时间单位为微秒时；为温度；为室温；为熔化温度。材料模型参数见表1所示。

表1 Al2024-T4的Johnson-Cook模型材料参数^[15]

对于压缩态：Mie-Gruneisen状态方程能够在一个很宽的压力和密度范围内对超高速碰撞中金属材料的行为进行准确描述。具体表述如下：

（3）

对于膨胀态：

（4）

上式中：为材料密度；C为材料声速；为Gruneisen参数；，，为（冲击波波速－波后质点粒子速度曲线）曲线拟合参数，通常，为0；是对的修正系数；为压缩度，定义为；为初始内能。状态方程参数如表2所示。

表2 Al2024-T4的Mie-Gruneise状态方程参数^[15]

2、数值方法的有效性验证

为了验证本文所采用数值方法及材料参数的准确性，采用直径为9.53mm的铝合金球形弹丸超高速撞击铝合金靶板，与文献中的试验结果进行了比较，数值模拟与试验条件参数相同。为了便于结果比较，将碎片云的特征速度定义如下：弹丸材料前端速度、弹丸材料后端速度，具体参见图3所示。

图3 碎片云特征速度示意图

图4~图7分别是不同速度及靶板厚度条件下碎片云的形态与试验结果对比图,从中可以看出数值模拟得到的碎片云形态与试验结果基本一致。将实验特征速度与数值仿真的特征速度统计如表3所示。

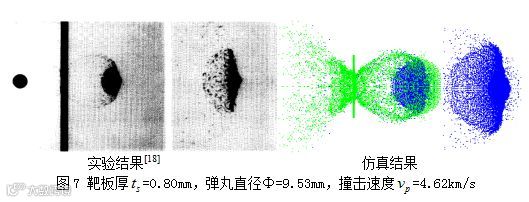
从表3中的结果可以看出，针对不同的试验结果，碎片云两个主要特征速度的数值仿真结果与实验测得的结果吻合较好，最大的相对误差不超过5%，从而验证了数值计算方法的有效性。

3、Whipple防护板的毁伤特征

碎片云团实际上是一个薄壳空泡，几乎所有碎片云都集中在薄壳云团前半部分。碎片云团由三部分组成，如图8所示。区域1为主碎片云团，由靶板（绿色部分）和弹丸材料（蓝色部分）组成，以弹丸材料为主；区域2为碎片云颈部，由弹丸和靶板材料组成，主要为靶板材料；区域3为反溅碎片云，主要由靶板材料组成。图9为哑铃型弹丸碎片云演化图，从图中可以看出，碎片云质量主要集中的主碎片云团；碎片云内部有两层结构，外层为靶板材料，内层为弹丸材料；碎片云在演化过程中，呈椭球形不断的向外扩张和膨胀。

图8 碎片云结构图

图9 哑铃型弹丸碎片云演化图

哑铃型弹丸超高速撞击防护板后，前板损伤的主要特征是在前板留下弹坑，近似呈圆形，用弹孔直径D表征前板的毁伤特征，见图10所示。

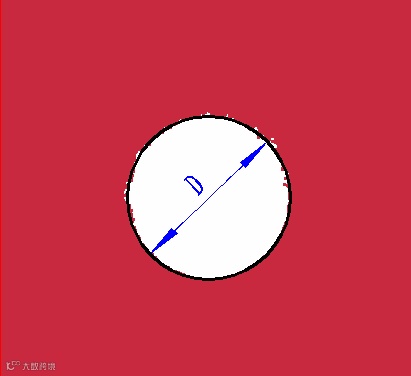
图10 前板毁伤特征参数

后板损伤的主要特征是后板受碎片云撞击形成通孔，成为中心弹坑区；在中心弹坑区周围存在很多微弹坑群，微弹坑群连成一片，形成环切带，成为环形弹坑区；碎片云在后板上形成一定的覆盖范围，成为碎片云覆盖区。碎片云覆盖区近似呈圆形，为碎片云对后板毁伤的最大区域，用毁伤直径表征，表征后板的毁伤特征，见图11所示。

图11 后板毁伤特征参数

4、前板毁伤特性影响因素

4.1 撞击速度对前板撞击特性的影响

图12为哑铃型弹丸在不同撞击速度条件下前板弹孔图，图12（a）~图12（f）对应撞击速度分别为2.83km/s，3.77 km/s，4.71 km/s，5.45km/s，6.62km/s，7.38km/s，前板厚度取0.8 mm，规格为40mm×40mm，后板厚度取1mm，规格为60mm×60mm，板间距取30mm。图13给出了在不同撞击速度条件下，前板弹孔直径的变化情况。从图中可以看出，随着撞击速度的增加，前板弹孔直径增大。在撞击速度为2.83km/s时，前板弹孔直径D为1.35cm，约为弹丸直径的1.61倍；在撞击速度为7.38km/s时，前板弹孔直径D为1.50cm，约为弹丸直径的1.79倍；撞击速度增加约1.61倍，前板弹孔直径增加0.11倍。

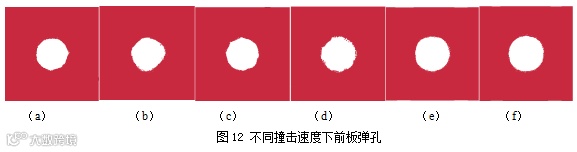
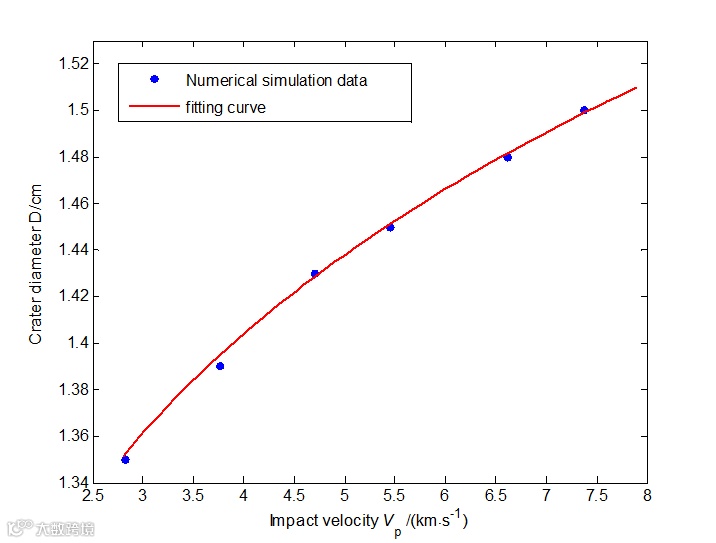
图13 撞击速度对前板弹孔直径的影响

4.2 前板厚度对前板撞击特性的影响

图14为哑铃型弹丸在不同前板厚度条件下前板弹孔图，图14（a）~图14（e）对应前板厚度分别为0.6mm，0.8mm，1.0mm，1.2mm，1.4mm，撞击速度为6.62 km/s，前板规格为40mm×40mm，后板厚度取1mm，规格为60mm×60mm，板间距取30mm。图15给出了在不同前板厚度条件下，前板弹孔直径的变化情况。从图中可以看出，随着前板厚度的增加，前板弹孔直径增大。在前板厚度为0.6mm时，前板弹孔直径D为1.41cm，约为弹丸直径的1.68倍；在前板厚度为1.4mm时，前板弹孔直径D为1.61cm，约为弹丸直径的1.92倍；前板厚度增加约1.33倍，前板弹孔直径增加0.14倍。

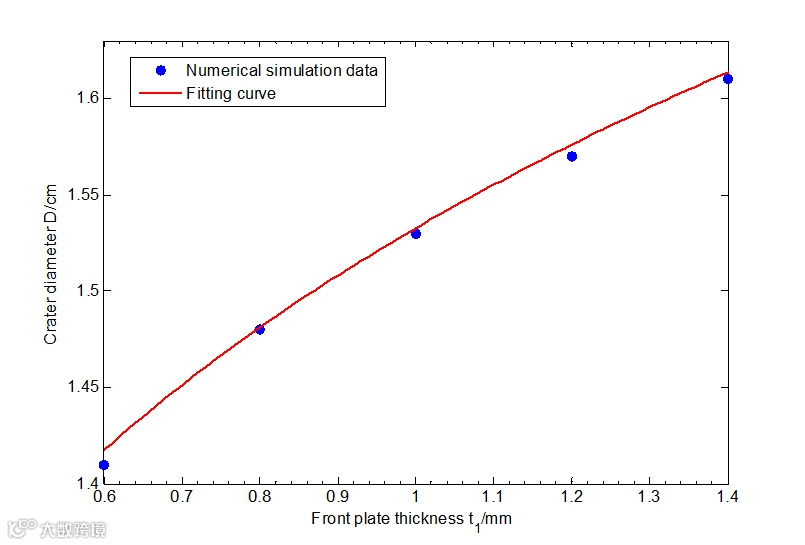
图15 前板厚度对前板弹孔直径的影响

5、后板毁伤特性影响因素

5.1撞击速度对后板毁伤特性的影响

图16为哑铃型弹丸在不同撞击速度条件下后板毁伤图，图16（a）~图16（f）对应撞击速度分别为2.83km/s，3.77 km/s，4.71 km/s，5.45km/s，6.62km/s，7.38km/s。图17给出了在不同撞击速度条件下，后板毁伤直径的变化情况。从图中可以看出，随着撞击速度的增加，后板毁伤直径增大。在撞击速度为2.83km/s时，后板毁伤直径为3.36cm，约为弹丸直径的4.0倍；在撞击速度为7.38km/s时，后板毁伤直径为4.99cm，约为弹丸直径的5.94倍；速度增加约1.61倍，后板毁伤直径增加0.49倍。

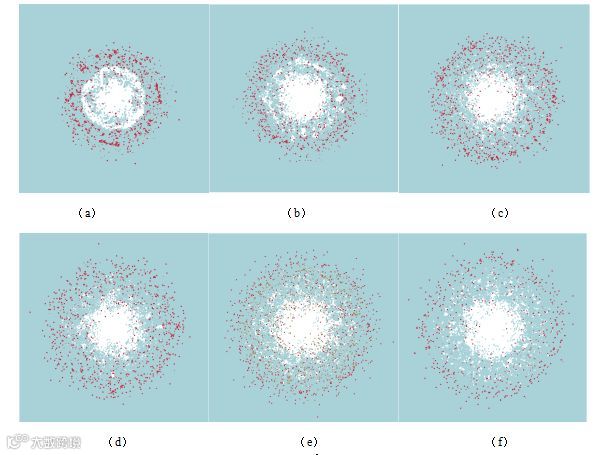
图16 不同撞击速度下后板毁伤特征

图17撞击速度对后板毁伤直径的影响

5.2前板厚度对后板毁伤特性的影响

图18为哑铃型弹丸在不同前板厚度条件下后板毁伤图，图18（a）~图18（e）对应前板厚度分别为0.6mm，0.8mm，1.0mm，1.2mm，1.4mm。图19给出了在不同前板厚度条件下，后板毁伤直径的变化情况。从图中可以看出，随着前板厚度的增加，后板毁伤直径减小。在前板厚度为0.6mm时，后板毁伤直径为5.13cm，约为弹丸直径的6.11倍；在前板厚度为1.4mm时，后板毁伤直径为3.98cm，约为弹丸直径的4.74倍；前板厚度增加约1.33倍，后板毁伤直径减小23%。

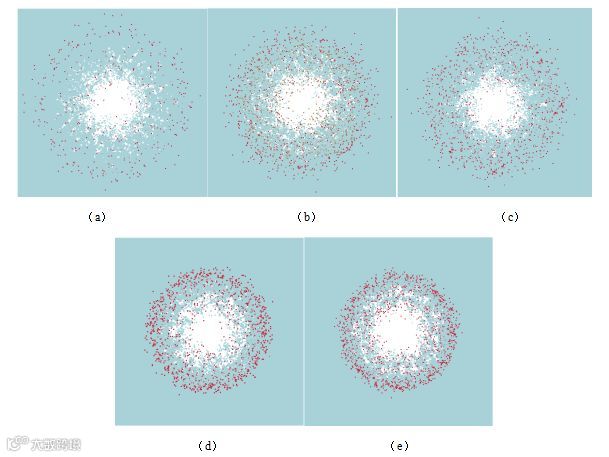
图18 不同前板厚度下后板毁伤特征

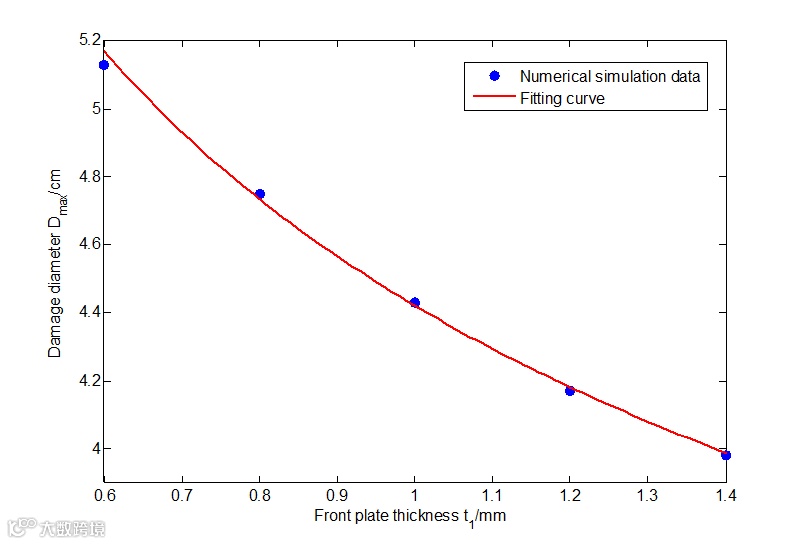
图19 前板厚度对后板毁伤直径的影响

5.3 板间距对后板毁伤特性的影响

图20为哑铃型弹丸在不同板间距条件下后板毁伤图，图20（a）~图20（f）对应板间距分别为10mm，15mm，20mm，25mm，30mm，35mm，撞击速度为6.62km/s，前板厚度取0.8 mm，规格为40mm×40mm，后板厚度取1mm，规格为60mm×60mm。图21给出了在不同板间距条件下，后板毁伤直径的变化情况。从图中可以看出，随着板间距的增加，后板毁伤直径增大。在板间距为10mm时，后板毁伤直径为2.70cm，约为弹丸直径的3.21倍；在板间距为35mm时，后板毁伤直径为5.18cm，约为弹丸直径的6.17倍；板间距增加2.5倍，后板毁伤直径增加0.92倍。

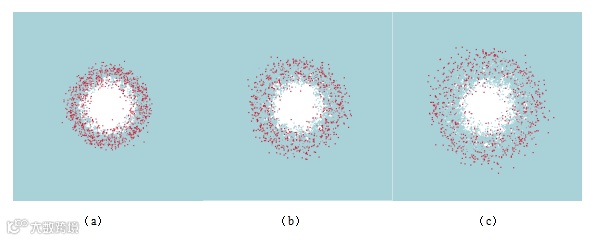
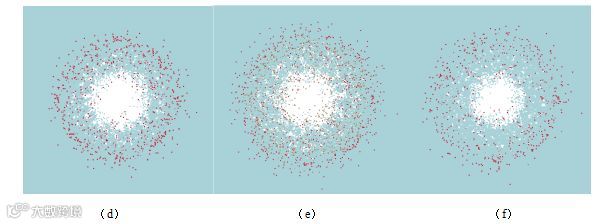
图20 不同板间距下后板毁伤特征

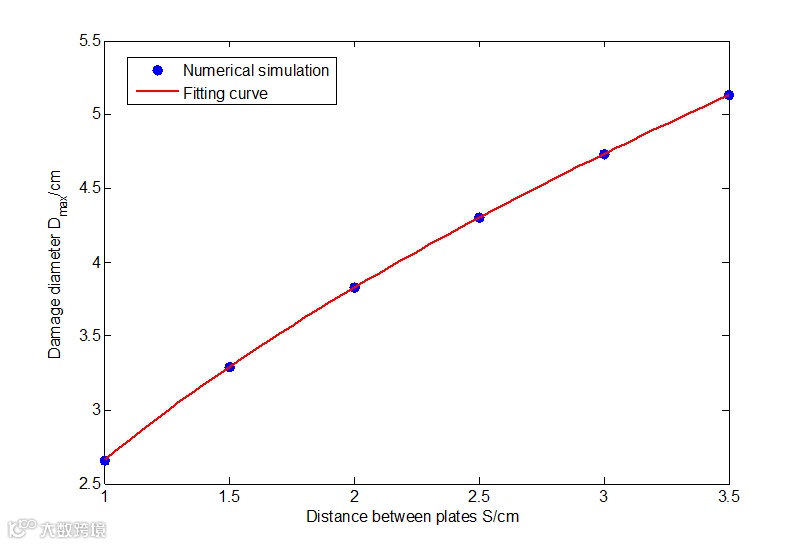
图19 板间距对后板毁伤直径的影响

6、结语

本文以空间碎片防护为研究背景，基于SPH方法，首先对直径为9.53mm的铝合金球形弹丸超高速撞击防护板进行了数值模拟，对碎片云形状及其特征速度与试验结果进行比较，两者吻合的很好，从而验证数值仿真方法的有效性。本文选取的Johnson-Cook材料模型、Mie-Gruneisen状态方程能较好的模拟碎片云的形成、演化以及扩展运动情况。随后开展哑铃型弹丸超高速正撞击Whipple防护板的数值仿真分析，对防护板前板和后板的毁伤特征进行分析讨论，主要结论如下：

（1）撞击速度对前板弹孔直径和后板毁伤直径影响较大。随着撞击速度的增加，前板弹孔和后板毁伤直径增大。在相同条件下，撞击速度增加约1.61倍，前板弹孔直径增加0.11倍；后板毁伤直径增加0.49倍，撞击速度对后板的毁伤特性的影响大于前板。

（2）前板厚度对前板弹孔直径和后板毁伤直径影响较大。随着前板厚度的增加，前板弹孔直径增大，后板毁伤直径减小。在相同条件下，前板厚度增加约1.33倍，前板弹孔直径增加0.14倍；后板毁伤直径减小23%。

（3）板间距对后板毁伤直径影响较大。随着板间距的增加，后板毁伤直径增大。在相同条件下，板间距增加2.5倍，后板毁伤直径增加0.92倍。

参考文献

[1] 龚自正, 韩增尧，庞宝君. 空间碎片防护研究现状与国内发展建议[J]. 航天器环境工程, 2010, 27(1): 24-31.

[2] 张伟，庞宝君，邹经湘等. 航天器微流星体及空间碎片防护方案[J].哈尔滨工业大学学报，1999，32(2): 18-22.

[3] 张庆明,黄风雷.超高速碰撞动力学引论[M]. 北京：科学出版社，2000.

[4] 张伟,庞宝君,邹经湘等.航天器微流星和空间碎片的防护方案.哈尔滨工业大学学报,1999,31(2):18-22.

[5] A.J.Piekutowski.Debris Clouds Produced by the Hypervelocity Impact of Non-Spherical Projectiles. International Journal of Impact Engineering. 2001,26: 613-624.

[6] 管公顺,朱耀,迟润强.铝双层板结构撞击损伤的板间距效应实验研究.材料科学与工艺,2008,16(5):692-695.

[7] 柳森,李毅.Whipple防护屏弹道极限参数试验.宇航学报,2004,25(2):205-207.

[8] Enrico Corvonato,Roberto Destefanis,Moreno Faraud.Integral Model for the Description of the Debris Cloud Structure and Impact.International Journal of Impact Engineering,2001,26:115-128.

[9] 崔伟峰,曾新吾.超高速碰撞数值模拟的工程算法模型.宇航学报,2004,28(1): 136-140.

[10] V.S.Hernandez,L.E.Murr,I.A.Anchondo.Experiment Observations and Computer Simulations for Metallic Projectile Fragmentation and Impact Crater Development in thick Metal Targets. International Journal of Impact Engineering. 2006,32: 1981-1999.

[11] 胡震东,黄海,贾光辉.超高速撞击碎片云特性分析.弹箭与制导学报,2005, 26(1): 747-749.

[12] S.J.Hiermaier,F.K.Schafer.Simulation of Ellipsoidal Projectile Impact on Whipple Shields.International Journal of Impact Engineering Journal of Impact Engineering, 2003,29:333-343.

[13] Kuifeng Hu,W.P.Schonberg.Ballistic limit Curves Non-Spherical Projectiles Impacting Dual-wall Spacecraft Systems. International Journal of Impact Engineering. 2003,29:345-355.

[14] 陈沿海, 张庆明，黄风雷. 超高速斜撞击碎片云膨胀运动的SPH数值模拟. 第八届全国爆炸力学学术会议论文集,340-346.

[15] Hu K F, Schonberg w P. Ballistic limit curves for non-spherical projectiles impacting dual-wall spacecraft systems[J].International Journal of Impact Engineering, 2003,29:345-355.

[16] 蒋彩霞.超高速撞击碎片云损伤建模[D].哈尔滨:哈尔滨工业大学,2007.

[17] Dominique Lacerda,Jean-Luc Lacome.Simulations of Hypervelocity impacts with smoothed particle hydrodynamics[R].DYNALIS Report,Paris, Rrance, 2003.

[18] Kevin L.Poormon and Andrew J.Piekutowski. Comparisons of Cadmium and Aluminum Debris Clouds. International Journal of Impact Engineering,1995, 17:639-648.

作者简介：徐峰(1985-)，男，硕士，工程师。研究方向：舰船结构

2018年11月份培训安排

15日-17日北京第15届全国非线性有限元高级讲习班

扫描下方二维码下载讲习班报名表↓↓↓