摘 要:SiPESC.OPT是基于SiPESC研发的通用多学科优化集软件,是用于解决工程与科学计算中决策问题的集成优化工具。目前,该软件已经集成多种主流的优化算法库,支持多种试验设计和近似模型方法,成功解决了多个工程问题。本文介绍了近期SiPESC.OPT研究进展,包括1)基于SiPESC.Filter(过滤器图表)功能设计了直观易操作的交互界面,实现了优化问题及流程的快速定义和搭建、多种工程软件参数化过程中软件调用和数据读写自动识别、优化结果的可视化等功能,减低了软件的使用操作门槛。2)实现了计算盒子功能,提供多种软件调用支持,包括基于SiPESC平台SSH协议远程调用功能实现了优化任务计算的远程调用,为大规模计算和复杂流程提供更广泛支持。3)丰富了优化、试验设计、近似模型的算法库,其中,优化算法库提供了梯度算法NLPQLP和多目标算法NSGA2的支持、试验设计提供了最优拉丁方、Sobol和正交多项式相关取样方法、近似模型提供了正交多项式张量积和稀疏回归正交多项式算法。4)增加了田口试验设计、蒙特卡洛和JC法可靠性计算、6西格玛可靠性优化等品质设计功能。以上最新功能为SiPESC.OPT获得更广泛的应用提供了坚实的基础。
关键词:SiPESC.OPT、拖拽式图形界面、远程优化任务、NLPQLP优化、Sobol试验设计
0 引 言
多学科集成优化的原理是将探求多学科耦合的最优设计问题分解为基本的参数最优化问题。多学科集成优化最早应用在航天航空工程,飞行器设计中,需要集成多个学科的分析进行最优化设计,以获得更高性能[1]。航空工业飞机设计的发展对保证力学性能的减重设计需求急迫,首先推动结构优化快速发展。代表性的有Gerard[1]等提出的同步失效准则,由Schmidt[2]提出的满应力准则应用在板、外壳、框架梁、柱、以及加筋等飞行器结构中,大幅度提升了飞行器性能。航空工业对结构优化的研究工作为集成优化研究奠定了基础。
二十世纪随着有限差分方法、有限元方法、数学规划方法和计算机技术的发展,数值仿真广泛应用于各个学科领域。航天航空工业中的优化问题也不再是单一的结构优化问题,要求集成多个学科的仿真分析,对系统整体的性能进行设计。例如飞行器优化设计中,需要同时考虑包括空气动力学,结构,推进和控制等学科,最优设计成为综合考虑各学科性能要求的多学科集成优化设计[3]。另外,在汽车[4]、高速列车[5]、船舶[6]、海洋工程[7]等领域也提出了大量的多学科集成优化设计需求。从此,多学科集成优化设计的需求和研究进入一个新时期。
在过去的半个世纪里,科研人员提出了多种算法用于解决多学科集成优化问题[8]。最优化算法方面:发展了多种有效的优化算法,包括SQP、MMA、ACO等。解决复杂问题求解困难问题时,发展了多种有效的近似模型算法,Cheng[9]等对具有全局近似功能的近似模型研究工作做了回顾,给出了常用代理模型的优缺点。另外,针对包含误差及未知因素的不确定性模型,发展了多种不确定性优化算法,姜潮[10]等对现有的不确定性优化算法进行了总结和回顾,并给出区间类不确定性优化算法时具有的优势。
随着各学科仿真软件计算性能的提升和需求的多样性增多,科研及软件工程在多学科集成方面提出了多种有效的计算机辅助技术。发展了多种软件数据格式的转换工具和服务,包括各类仿真软件的数据转化、各种不同软件输入输出格式的标准化,多领域软件数据交互的格式定义等[11]。发展了多种用于集成算法和计算模型的软件设计模式,包括编程中的面向对象编程、面向服务编程等;包括软件设计中的工厂设计模式、建造者设计模式等;包括面向科学及工程软件设计中的“模型+算法+参数”设计模式等。发展了大规模并行计算和远程高性能集群调用用于提升多学科仿真问题的计算能力[12, 13]:大规模仿真计算可以使用MPI和OpenMP等技术实现并行来缩短计算用时;多个地区都研发和建设用于科学计算的超级计算机,我国排名前列的有太湖之光和天河二号[14]等。
多学科集成优化设计是跨学科,跨专业的研究课题,需要计算机领域相关的辅助和研究工作。随着各学科领域研究工作的精细化和边界化,跨学科研究是不可避免的问题,而多学科集成优化设计已经在现代的各个尖端科学领域的到了广泛的深入发展和应用。多学科集成优化在近二十年来一直是计算力学跨学科的研究热点[15],并得到了进一步的深化与拓展;多学科集成优化方法在科研和工程领域也获得了广泛的应用,其重要性日益显著,也有很多亟待解决的问题和面临的挑战[16]。
本文介绍了通用优化计算软件SiPESC.OPT功能开发进展。SiPESC.OPT结合多学科优化对软件功能的需求,针对性的进行软件的研发。针对多学科优化问题事件表示进行规划和相应的实现,以适应多学软件集成和复杂问题表示;针对多学科优化使用到的基础数值工具进行补充,以满足不同数值问题的求解对算法的需求;针对工程师对软件界面操作性需求设计了可拖拽式的优化搭建流程,实现了对流程图(Filter)的拖拽和配置搭建优化求解任务;针对工程师对任务制定化的需求开发了任务流程模板,使用预制的Filter模板配置文件可以快速修改搭建新的任务流程。SiPESC.OPT围绕解决多学科优化问题的出发点,不断提高本身软件的适用性和易用性。
1 多学科集成优化软件系统/程序设计
多学科集成优化设计可以提高产品设计各方面性能;而且更为重要的是,多学科集成优化设计是现代科学跨领域设计的关键技术,引领各领域综合技术革新。因此,科目前有大量的科研人员和工程师利用多学科集成优化技术对研究对象和产品进行优化设计,但大多数工作是基于国外成熟商用及开源软件实现的,如Isight[17]、Optimus[18]、Visual DOC[19]、ModelCenter[20]、DAKOTA[21]、OpenMDO[15]等。现代尖端跨学科研究、高端工业产品设计中离不开多学科集成优化软件,学科集成优化设计软件可谓是软件领域中的国之重器。因此需从构建高层次核心科研能力、强化学科优势地位的着眼,研发一个开放性的多学科集成优化软件系统,使其具备大规模计算能力、支持多人/多组织研发、具备算法与功能集成能力,可用于解决工程实际中的多学科集成优化问题。
多学科集成优化的研究是基于算法程序设计和现代软件工程开展的,涉及优化算法、多学科仿真分析(如空气动力学分析、结构力学分析、有限元分析、控制系统分析等)、软件集成调用、软件数据交换、高性能计算,是体现了科学计算与数值仿真软件开发和集成能力;因此,算法程序设计和现代软件工程在多学科集成优化研究中占有重要地位。目前在该领域的工作可以分为以下几类:
1) 基于Matlab软件(或Python工具库)的多学科集成优化计算
Matlab软件以其影响力吸引了一大批科研工作者在其之上展开多学科集成优化计算工作。Matlab软件提供了优化工具箱Optimization Toolbox[22],提供了多种近似模型生成工具如径向基网络、支持向量机近似的训练和分类函数[23]等;另外一些科研工作者开发了基于Matlab开发了优化算法程序(如MMA优化算法[24])、代理模型生成工具箱(如dace[25]、ooDACE[26]),不确定性分析工具箱UQLab[27]等。使用Matlab为科研带来了便利,但其计算规模和多学科集成能力受限制,没有针对各学科工程软件集成开发的专用工具和接口,缺少软件数据处理的专用工具和远程调用等处理软件集成固体工具,在工程中使用受限。基于Python的工具库(如SMT[28])同样在科研中有着广泛的应用和吸引力,但在工程项目中因同样的问题失去了便利性和的受欢迎程度。
2) 自主研发的多学科集成优化软件/程序
研究工作基于已完成的科研项目代码,通过已有的Fortran、C、C++等面向对象语言研发的结构分析软件/程序,或者开源的结构分析软件开展。采用面向对象的算法语言的实现,可以在某些特定的学科、特定的工程问题一定程度上扩展计算能力,解决部分多学科集成问题。但由于软件构架和开发模式受限,随着算法研究的深入、软件功能的扩展或者研究团队扩大,对功能代码的调整、修改、维护和扩展工作量将成为严重问题。同时,这些软件缺乏具有广泛集成性和能提供各种辅助多学科集成优化所需的各种工具,而这些工具的开发依赖软件技术的发展和软件基础平台的构建。
3) 基于商用仿真软件平台已有的功能进行二次开发
目前提供多学科集成优化设计的商用仿真软件包括ANSYS Workbench、MSC SimXpert等。在这些平台基础之上,采用各自软件平台提供的多学科领域的软件工具带来极大方便,数据交换也会方便。如ANSYS除了结构有限元分析外,还提供了流体分析Fluent、电磁场仿真Maxwell等丰富的学科领域;通用Workbench提供的参数集、提供的Python和APDL等脚本语言可以实现多学科领域集成优化,但其优化功能和近似模型建模功能有一定局限性,二次开发会受到商用软件开放程度的制约。另外,这些软件平台中集成的其它学科仿真分析功能各有优势,应用领域和场合不同,集成多家商用仿真软件的部分功能,在数据交互和任务流程驱动上存在一定的困难。
SiPESC.OPT的研发工作根据本领域的软件系统和程序设计的主要工作模式进行调整,目前在不断的完善现有的辅助工具,并创建具有集成通用工具的环境,以满足更复杂多学科优化设计的需求。在软件模式中,也搭建了适用于多人/多组织协同开发的开发环境,使得用户更便于引进更先进的软件开发技术,提供先进的软件工具及功能。这样可以使得研究者不束缚于软件技术/工程的限制,把有限的时间从多学科集成工作中解脱出来,减少重复编写软件执行任务流程和数据读写交换,将精力集中在本领域的多学科优化问题。
2 多学科集成优化的主要内容
2.1 多学科集成优化的关键环节
多学优化的关键环节是指导了SiPESC.OPT开发方向和重点开发内容。多学科集成优化研究中的关键问题是如何建立合理的多学科集成优化问题模型,虽然不同学科有所差异,主要环节有:
1) 学科分析
学科分析手段是保证多学科集成优化设计的基本环节。各学科需要通各自的仿真软件、或试验数据模型等建立该学科的分析模型。优化体系对学科分析模块最基本的要求是高精度、高可信度、高效率,然而这几个基本要求之间往往是相互矛盾的。学科分析需要权衡精度、可信度和效率的问题,通过本学科的各种计算的优劣势和科研工程人员的经验,选择最适合于整体集成优化设计的求解策略[29]。
2) 参数化建模
参数化建模是保证多学科集成任务流程的重要环节。一般的参数化建模中,可以利用软件本身的宏或者脚本工具实现几何建模、仿真分析等过程的参数化。参数化的过程需要根据需求进行选择,对学科分析影响较小/或者比较独立的仿真分析选择参数,可以在导入打开已有数据/模型/仿真过程等学科分析的基础上,设计改变这些参数即可,例如修改界面几何尺寸、选择材料常数;对于影响较大/或者影响其它学科分析的参数,需要对某一个软件操作过程进行参数化/脚本化,例如网格重新划分,APDL实现的整个分析流程;对于更为复杂的建模和过程,则需要研发专用的工具进行参数化建模,例如使用Nurbs、Bezier曲面对船舶[30]和机翼外形进行参数化建模[31]。参数化方法需要解决特殊仿真分析的兼容性和独立性,需要解决多学科/多流程集成软件数据交互的可行性等问题[29]。
3) 敏度分析
多学科集成优化过程中会用到梯度优化算法,需要对变量进行灵敏度分析。灵敏度分析通常指目标函数或约束函数相对于设计变量或参数的导数。目前有许多不同的灵敏度分析方法, 包括手工求导法、符号微分法、有限差分法、自动微分法、复变量法、解析法、半解析法、伴随法等[32]。
4) 优化模型建立和算法选取
优化模型的建立会直接影响多学科集成优化设计的效果。优化模型中需要合理的选择设计变量、目标函数和优化算法这3个基本要素。一般情况下,目标和约束变量的选择较为直接,是本学科关注的问题,比如飞行器的气动性能、汽车的安全性和舒适性等;但选取后需要经过一定的处理,比如梯度算法中对目标和约束的归一化、智能算法中对约束处理的罚函数法等。设计变量的选择需要考虑参数化的可行性、目标/约束对其的灵敏度,变量对计算效率的影响等因素。优化算法的选择需要考虑问题的非线性复杂程度,综合考虑效率和质量的矛盾权衡,以及算法实时的其它因素等[29]。
5) 近似模型问题事件表示
近似模型又称为代理模型,它使用近似的数学模型,在损失一定精度的前提下将复杂的学科仿真过程分离出来;或者它可以在无法建立仿真模型的情况下,通过样本构建响应变量与输出变量的关系。近似模型可以通过已知点的响应信息来预测未知的响应值,在降低多学科优化集成优化设计的复杂性中起到了关键作用[8, 33]。
6) 优化流程求解及控制
多学科集成优化需要调用各学科中的仿真分析软件,自有程序和商业软件需要提供5个基本元素:运行空间内输入变量的新值、输入变量对应软件执行的模型或者脚本输入方式、仿真软件启动和模型的初始化、仿真结束后模型运行空间处理、运行空间内输出变量取值得获取。大量科研人员针对本学科专业及需要使用的软件进行流程搭建,如使用UG+ADAMS+ANSYS+Matlab用于机械设计的流程[34]、使用SolidWorks+ICEM+CFX-Pre+CFX-Solver+CFX-Post的汽轮机设计流程[35]等。
2.2 多学科集成优化的主要技术
为了克服多学科集成优化流程搭建中商业软件数据交换的问题,目前很多科研人员开发了多种数据转化的程序和工具,用于解决不同多学科集成优化设计的数据交换需求;如流固耦合中将流体计算的压力转化为固体计算的载荷,将ANSYS结构有限元进行模态分析生成ADAMS使用的柔性体模态中性文件*.mnf等、ANSYS、Nastran、ABAQUS等结构分析结果的读取。Aget[36]在欧洲多学科优化会议的总结中指出了该领域对软件集成的需求。Van Gent[37]为多学科集成优化数据交换设计标准传输格式。
多学科集成优化中,科研和工程人员会使用远程服务器或者超级计算机实现高性能计算。刘婷[13]在文献中指出高性能计算已成为航空发动机研发所必须的关键技术,张月玲[38]指出航空领域的气动计算(CFD)、结构力学计算、雷达隐身设计计算、噪声计算、燃烧问题计算、结冰模拟计算、气动弹性计算都有在高性能计算的需求突出。这些远程超级计算机的使用,需要提供本地客户端,完成远程的软件调用及数据传输管理。
多学科集成优化设计中,需要提供优化算法和代理模型算法功能的软件,并提供友好的操作界面,这也是关键技术之一。学者们针对优化算法和代理模型进行了很多研究,提高优化算法的效率和代理模型近似的精度。在很多学科领域,科研人员/团队开发了专用的优化软件和代理模型分析软件[9]。
为了评估参数中的不确定性给多学科集成优化的影响,发展不确定性估计算法和不确定性优化的算法也引起了很多科研工作者的重视。包括概率类方法(如蒙特卡洛[39]、概率凸模型[40]),非概率类的方法(如证据理论[41]、多项式区间估计[42])。也有科研工作者发展了用于不确定性分析的软件(如OpenTURNS[43]、OpenCossan[44])
上述工作表明,辅助多学科集成优化的技术和工具已成为该领域发展的重要方向,对保证多学科集成问题事件表示、优化模型合理性、求解稳定性、计算效率具有重要作用。
3 SiPESC.OPT研发进展
SiPESC.OPT研发的方向是通过构建开放式的通用多学科集成优化设计系统,建立支持协同开发的面向服务软件系统动态服务接口和管理机制,集成多学科集成优化设计的基础算法,实现丰富的面向通用工程的领域多学科集成优化的辅助工具,实现大规模多学科集成多任务流程并行/分布式计算仿真优化设计问题的计算。根据多学科集成优化各个关键环节的需求出发,SiPESC.OPT不断推进功能的研发,主要进展在一下几个方面。
3.1 计算盒子功能
优化问题中的重要环节是软件集成调用,它关系到问题事件的表示和优化流程的控制和求解。优化求解过程其实是将“表示问题事件的计算”迭代的过程,可以将“表示问题事件的计算”理解为黑箱子,考虑其输入、输出、计算、控制执行和信息输出,使用“计算盒子”对其进行抽象和表示。这样所有的软件集成调用的支持,可以归结为对应软件“计算盒子”的开发,而优化任务求解直接面对通用的“计算盒子”的接口进行,通过调用其计算任务实现优化迭代过程。
经过对仿真软件调用的逻辑抽象,设立管理器(CalculationBoxManager)、计算器抽象工厂(CalculationBoxFactory)、计算器配置(CalculationBoxConfig)、计算器盒子(CalculationBox)、计算器应用(CalculationBoxApplication)管理五个方面的抽象服务实现应用程序管理。以ANSYS Workbench为例各服务对应的接口UML关系如下图所示:

图1 计算盒子功能UML图
Fig. 1 UML diagrams of calculate box function
使用ANSYS Workbench计算盒子时,只需要通过ANSYSWorkbenchCalculationBoxConfig配置给定变量相关配置和运行相关配置,计算盒子ANSYSWorkbenchCalculationBox完成所有的数据交换和软件调用。
目前已经实现的软件调用包括脚本计算盒子Javascript\Python\CScript(类似于C语言描述的数学表达式)、CAD计算盒子UG、仿真计算盒子ANSYS Workbench、一般应用程序执行计算盒子LocalApplication和Launch(通SiPESC提供的执行工具配置执行)、批处理执行计算盒子CMD、远程应用程序执行计算盒子SSH、多种类型计算盒子组合顺序执行的多任务计算盒子Multiple。后续根据用户的需求和软件的提升,会有更多计算盒子增加实现更多软件集成数据的自动化识别读写交互,现有计算盒子也会不断的完善输入输出的识别读写能力。同时计算盒子功能也提供了界面,可以通过界面配置和完成计算过程,可拖拽的图表见图4左侧。

图2 多任务计算盒子调用Python代码
Fig. 2 Python code of multiple calculate box function
多任务计算盒子通过脚本调用示例如图2所示,其运行过程数据变化如所示。多任务计算盒子的示例展示了SiPESC.OPT计算盒子功能的灵活性和通用性。

图3 多任务计算盒子执行过程中数据变化
Fig. 3 Data changes in running process of multiple calculate box function
3.2 拖拽式Filter图形界面
通过拖拽方式搭建优化流程是符合工程师使用习惯的方式,是开展多项集成优化软件工程应用的重要工具。SiPESC.OPT实现了通过拖拽搭建优化流程、DOE流程,同时支持优化结果可视化查看、支持通过模板快速搭建各种已有流程。
优化流程搭建中需要拖拽“优化模型OptModel”、“优化求解器OptSolver”和“问题事件表示的计算盒子”进入编辑器,然后在编辑器通过连接Filter模块的信号和输入输出完成“信号+数据流”双驱动的任务流程搭建。搭建好的UG+ANSYS Workbench优化流程如图4所示。其中UG的配置界面如图4所示,可以通过导入UG的*.prt识别UG中可直接作为参数的变量,并拾取为优化设计变量。

图4 SiPESC.OPT搭建的UG联合ANSYS Workbench优化流程
Fig. 4 Optimization task combining with UG and ANSYS Workbench constructed by SiPESC.OPT

图5 UG自动识别*.prt中参数并拾取设计变量界面
Fig. 5 Automatic variables parsing and picking GUI for UG part file “*.prt”
DOE流程搭建需要拖拽“优化模型OptModel”、“优化求解器OptSolver”、“试验设计模型”、“试验设计生成器”、“近似模型生成器”和“问题事件表示的计算盒子”进入编辑器,然后在编辑器连接Filter模块的信号和输入输出任务流程搭建。
SiPESC.OPT的图形界面提供了查看优化迭代结果的数据可视化工具。可视化工具中目前支持绘制散点、样条曲线、连线、折线、柱状图、点加线、3D散点、3D轨迹、3D曲面、二维表。例如多目标计算的结果可以通过绘制图表显示,如图6所示显示了Kursawe测试函数经过NSGA2多目标优化算法求解后的Pareto最优解边界和所有求解的多目标结果。

图6 多目标优化算法Kursawe函数测试结果绘图
Fig. 6 Scatter plot for test result of multi-objective optimization problem with Kursawe function
SiPESC.OPT提供模板创建功能,预置了优化模板、试验设计模板、代理模型模板、DOE模板,同时也支持通过已搭建流程创建自定义的模板。优化模板创建流程如图7所示,模板创建后拖入“问题事件表示的计算盒子”进入编辑器即可快速搭建优化需要的Filter,配置优化问题后即可运行,通过模板功能可以实现多层优化问题嵌套,复杂多层任务的搭建。

图7 SiPESC.OPT中GUI创建优化任务流程模板
Fig. 7 The creation of optimization task module in SiPESC GUI
3.3 增加算法功能
SiPESC.OPT为了提高作为集成优化软件的基本功能,对算法求解库进行补充。优化算法方面提供了算法库NLPQLP、多目标算法算法NSGA2,试验设计增加Sobol方法,近似模型提供了正交多项式张量积和稀疏回归正交多项式算法。

图8 Python调用NLPQLP优化算法求解盒子优化问题
Fig. 8 Python code of solving box design problem using NLPQLP optimization solver
NLPQLP算法库是用于求解光滑非线性规划问题的序列二次规划算法,具有较高求解效率和的精度[45]。NLPQLP优化算法可以在初始设计点附近进行充分的寻优,对于约束非线性问题求解具有较强的稳定性和收敛性。使用Python调用NLPQLP算法完成盒子优化计算代码如图8所示,盒子优化是问题是长、宽、高作为设计变量,体积小于1,让其盒子用料面积最小,最优解是长和宽取1,高取2,盒子用料面积为12。
多目标优化方面,SiPESC.OPT新研发了针对智能类算法的集成框架,可以轻松地扩展新的智能类算法,特别是基于智能类方法迭代,选择Pareto最优解边界完成多目标最优求解的算法。SiPESC.OPT首先选择最常用的NSGA2算法进行集成。支持通过脚本和软件界面进行调用,软件界面的调用通过配置相应的Filter活动流程图完成,脚本调NSGA2算法求解Kursawe函数的Python代码如所示。

图9 Python调用NSGA2优化算法求解Kursawe问题
Fig. 9 Python code of solving Kursawe problem using NSGA2 optimization solver
Sobol是一类重要的低偏差序列,利用它可以生产更均匀的试验设计样本点。低偏差序列是指空间中点集偏差趋近于0的序列,偏差使用表示,定义为
 (1)
(1)
其中,为空间内任意区域的表示,为该区域内点的数量,为空间总点数,为空间区域的体积。偏差越低,代表序列分布越均匀。Sobol序列是以2为基的序列[46],且整数。Sobol序列是基于一组叫做方向数而构造的。设是小于正奇数,则
 (2)
(2)
数和的生成借助于系数只为0或1的简单多项式,该多项式也被称为本原多项式,表示成:
 (3)
(3)
本原多项式为不可约多项式。对 有递归公式
 (4)
(4)
这里表示二进制按位异或运算符,如11=0,00=0,10=1。对于的递归公式是
 (5)
(5)
根据方向数可以得到sobol序列的第i个数为:
 (6)
(6)
其中,是i的二进制表示形式。
Sobol序列的生成Python代码如图10所示,取4个设计变量,1000个样本,变量取值范围为,生成的试验设计样本两个维度的结果如图11所示,结果显示样本分布均匀。

图10 Python调用Sobol序列方法生成试验设计样本
Fig. 10 Python code of create experiments design samples using Sobol series

图11 Sobol试验设计生成的样本
Fig. 11 Experiments design samples created by Sobol series
3.4 品质优化设计
SiPESC.OPT提供了品质优化设计功能,包括概率和非概率可靠性设计的解决方案、鲁棒性设计的解决方案。品质优化设计用于考虑不确定性对产品性能和品质的影响,可以将生产或使用过程中的风险降到最低。具体功能包括田口稳健性设计、可靠性计算、6西格玛优化。
SiPESC.OPT提供田口稳健性设计使用了已有试验设计功能如图12所示,其中第5-11行使用正交试验设计生成噪声因子的试验设计样本,第13-23行使用正交试验设计生成控制因子的试验设计样本。另外,第10-41行创建Python计算盒子配置并初始化给田口试验设计用于结果分析。田口试验设计的软件界面正在开发中。

图12 Python驱动实现田口试验设计
Fig. 12 Python code to accomplish the task of taguchi experiment design
SiPESC.OPT提供的可靠性设计中,提供而蒙特卡洛和JC法(提供FORM和SORM)方法,输入随机变量的分布类型支持:Bernoulli、Binomial、Negative-Binomial、Poisson、Geometric、Uniform、Exponential、Weibull、Normal、Log-normal、Chi-squared、t、F、Erlang等概率分布类型。使用代码演示如图13所示。可靠性计算过程中,通过第20行添加可靠性模型的响应实现可靠性编辑类型的添加和选择,通过第25行参数选择是用蒙特卡洛或者是JC方法。在计算过程中,尤其是JC法中,可以28行输入精确的极限状态方程表达式,这样可以获得更为精确有效的可靠度结果。

图13 Python驱动实现可靠性计算
Fig. 13 Python code to accomplish the task of reliability calculation

图14 Python驱动实现六西格玛可靠性优化
Fig. 14 Python code to accomplish the task of six sigma reliability optimization
SiPESC.OPT提供的6西格玛可靠性优化设计,任务流程及调用过程如图14所示。6西格玛可靠性优化设计是在可靠性计算的基础上实现的,第3-29行是实现可靠性计算的配置,第31-42是实现6西格玛优化设计过程。其中第37-39行是设置极限状态西格玛优化目标,可以选取不同的类型和西格玛目标,约束6西格玛可靠性优化设计,达到不同的设计要求。
4 工程应用
4.1 起重机优化
履带式起重机(如图15所示)是通过动臂旋转实现作业的起重机,桁架式臂架具有承载能力强、重量轻等优点。使用SiPESC.OPT对履带起重机不同工作幅度下极限吊载的工况,分别对其进行优化,降低腹板和腹杆的应力。结果如图16所示,与初步设计相比较,腹板应力从905.745MPa降到335.019MPa,腹杆应力从455.938MPa降到215.605MPa。

图15 超起工况履带起重机
Fig. 15 The crawler crane with superlight

图16 超起工况履带起重机优化结果
Fig. 16 Optimization result of crawler crane with superlight
4.2 跨平台回归桥梁优化
基于SiPESC.OPT与SiPESC提供的Python机器学习框架下,实现了SiPESC.OPT与机器学习框架的联合优化,流程分为试验设计表生成、机器学习模型训练和最优化设计三个模块。如图3.10所示的典型梁结构算例,通过试验设计、回归模型分析和优化计算的完整分析流程搭建了该优化流程。

图17 简易梁结构
Fig. 17 Simple beam structure
这一简单的梁单元模型总跨度为,跨高,在上端分别受到向右下45°、向下和向下的大小为、和的集中力作用,左右两端除转动外全部约束。梁单元截面为矩形截面,将高度H和宽度W作为优化问题的设计变量,目标为整体结构的轻量化,并且施加有最大应力和高度H的约束条件。
表1 SiPESC.OPT优化结果
Tab. 1 SiPESC.OPT Optimization Results
B |
H |
总重量 |
减重比 |
|
优化前 |
0.222 |
0.5576 |
16547.3 |
|
优化后 |
0.1486 |
0.3001 |
7046.34 |
57.25% |
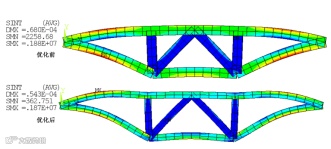
图18 优化前后结构应力分布图
Fig. 18 Stress distribution of structure before and after optimization
优化前后参数如表1所示,结构的应力云图比对如图3.13所示。可以看出,在满足约束条件的基础上,达到减重57.25%的实际效果,证明回归模型可以作为试验设计与优化设计间的纽带,用于整体优化流程的搭建。该流程的搭建具有高效性与准确性,可以推广到更多结构分析问题与多学科分析问题的优化设计求解中进行实践。
4.3 支架形状优化
工程支架底面由螺栓与整体连接固定如图19所示,顶端乘重部分受到连接件的过载压力,通过与连接件相接的螺栓孔传递所有4G过载压力。根据对称性,取一半建立有限元如图20所示,在沿着C1孔的对称截面施加对称约束,底端螺栓孔用于固定限制整体结构的转动自由度,施加固定端约束,在顶端螺栓孔的节点上施加节点力载荷。考虑重量最小化为优化目标,对开孔位置和大小进行优化,满足最大Mises小于210MPa和频率大于600Hz的约束,使用SiPESC.OPT和机器学习的回归模型建立代理模型,使用遗传算法进行优化。

图19 支架说明图
Fig. 19 Diagram of bracket structure

图20 (a)支架网格划分与载荷、约束施加图(b)支架主视图
Fig. 20 (a) Mesh, load and boundary distribution of bracket(b) main view of bracket
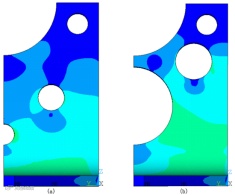
图21 支架优化前后结构应力分布图
Fig. 21 Stress distribution of bracket before and after optimization
表2 支架结构信息优化前后对比
Tab. 2 Comparison of bracket information before and after optimization

优化前后主视图下支架应力分布云图比对如图21所示,C1孔的开孔半径被增大,C2孔适当增大半径的基础上,孔心位置上移,合理的满足整体结构的约束条件。结构在优化后结果对比如表2所示,整体减重达到13.02%,基频略有提高,最大Mises应力维持在需用最大应力范围之内。
4.4 海洋浮体结构优化大型海洋浮体结构随着尺寸增加,要求其固有频率不能接近外海波浪的频率范围,避免共振产生疲劳失效。

图22 海洋浮体结构模型有限元分解图
Fig. 22 Structure finite element decomposition model of marine floating body
最终优化结果前后结构的一二阶模态比对如所示,第一阶频率由72.087Hz下降至约束下限72.05Hz,第二阶频率由72.241Hz提升至72.267Hz,优化目标由0.154Hz增加到0.217Hz,优化后共增加40.9%。

图23 优化前后一二阶模态
Fig. 23 First and second order modal diagrams before and after optimization
4.5 悬臂梁田口稳健性设计
悬臂梁模型如图24所示,系统包含7个控制因子、3个噪声因子和1个信号因子。控制因子为悬臂梁长度、悬臂梁宽度、悬臂梁厚度、线性弹簧刚度、线性弹簧刚度、弹性模量和作用力;噪声因子为作用力位置、材料特性不确定性和作用力效果;信号因子为支撑点位置。系统响应为端点挠度,望大特性。试验脚本如图12所示,最终试验次数为96次试验。优化后结果如表3所示。
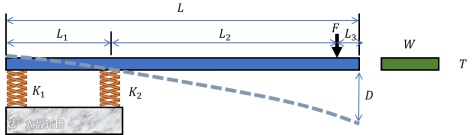
图24 悬臂梁模型进行田口试验设计
Fig. 24 The cantilever beam in taguchi experiment design
表3 优化后的悬臂梁参数
Tab. 3 Optimization result of cantilever beam
参数名 |
优化后的参数值 |
悬臂梁长度 |
114.0 |
悬臂梁宽度 |
24.0 |
悬臂梁厚度 |
2.0 |
线性弹簧刚度 |
1200.0 |
线性弹簧刚度 |
1200.0 |
弹性模量 |
1250000.0 |
作用力 |
200.0 |
4.6 JR608型机器人小臂可靠性计算
R608型六关节工业机器人小臂有限元模型如图25所示,主要用于搬运和焊接领域,最大负载为8kg。载荷分为小臂本体直接承载的载荷和小臂末端间接连接方式的载荷。其参数存在不确定性,概率分布如表4所示。通过响应面和JC法获得该输入参数下可靠度为β=9.4731,失效概率为Pf =1.357e-21。
表4 工业机器人小臂模型参数不确定性
Tab. 4 The uncertainty parameters of cantilever beam industrial robots forearm model
参数名 |
分布类型 |
均值 |
标准差 |
E |
正态 |
72000 |
2160 |
S |
正态 |
200 |
20 |
DENSITY |
正态 |
2.7E-9 |
8.1E-11 |
F |
正态 |
111.75 |
33.525 |
M |
正态 |
12.47 |
3.741 |

图25 工业机器人小臂有限元模型
Tab. 5 The FEM model of industrial robot forearm
5 结束语
本文介绍了通用多学科集成优化软件SiPESC.OPT研发的多项进展,主要包括拖拽式的图形界面、丰富的问题事件表示和远程调用、算法功能的增补、品质优化设计功能,软件的发展目标是构建开放式的多学科集成优化软件体系结构与设计方法。
各专业学科领域的算法研究和功能实现曾经引领专业仿真软件的发展,随着计算机硬件的发展和软件计算软件技术的发展,专业领域的发展方向更注重软件体系结构和设计模式等理论的发展,提出了面向对象/组件/服务的形式和设计思想,发展了针对专业仿真计算流程结合的软件设计模式,形成了新一代仿真软件的设计理念和方法论。多学科集成仿真优化软件设计也拥有同样的特性,也需要发展相应的软件设计模式和方法。其涌现的新问题是跨学科专业领域、具有较强的集成性,在此基础之上需要发展具有开放性和可扩展的多学科集成优化软件设计理论和方法,提出多学科集成软件设计的新标准、规范和模式,建立多学科集成优化设计计算平台。
参考文献
[1]GERARD G. Optimum structural design concepts for aerospace vehicles [J]. Journal of Spacecraft and Rockets, 1966, 3(1): 5-18.
[2]SCHMIT J, LUCIEN A. Fully-stressed design of elastic redundant trusses under alternative load systems [J]. Australian Journal of Applied Science, 1958, 9: 337-348.
[3]SOBIESZCZANSKI-SOBIESKI J. Multidisciplinary Design Optimization: An Emerging New Engineering Discipline [M]//HERSKOVITS J. Advances in Structural Optimization Solid Mechanics and Its Applications. Dordrecht; Springer. 1995.
[4]李铁柱, 李光耀, 顾纪超, et al. 汽车乘员舱安全性与舒适性多学科设计优化 [J]. 机械工程学报, 2012, 48(2): 138-45.
[5]MA S, ZENG T, CHU Y. Comprehensive Optimization Model of Diagrams of High-Speed Railway Express Freight Trains Operated in Passenger Train Patterns [Z]. International Conference of Logistics Engineering and Management. Shanghai; American Society of Civil Engineers. 2014: 327-34.10.1061/9780784413753.050
[6]DIEZ M, PERI D, FASANO G, et al. Multidisciplinary Robust Optimization for Ship Design [Z]. 28th Symposium on Naval Hydrodynamics. California; Office of Naval Research and the California Institute of Technology. 2010
[7]LUO W, LYU W. An application of multidisciplinary design optimization to the hydrodynamic performances of underwater robots [J]. Ocean Engineering, 2015, 104: 686-97.
[8]SOBIESZCZANSKI-SOBIESKI J, HAFTKA R T. Multidisciplinary aerospace design optimization: survey of recent developments [J]. Structural Optimization, 1997, 14(1): 1-23.
[9]CHENG K, LU Z, LING C, et al. Surrogate-assisted global sensitivity analysis: an overview [J]. Structural and Multidisciplinary Optimization, 2020, 61: 1187–213.
[10]姜潮, 韩旭, 谢慧超. 区间不确定性优化设计理论与方法 [M]. 北京: 科学出版社, 2017.
[11]DíAZ H, ALARCóN L F, MOURGUES C, et al. Multidisciplinary Design Optimization through process integration in the AEC industry: Strategies and challenges [J]. Automation in Construction, 2017, 73: 102-19.
[12]李根国. 高性能计算促进多学科优化设计发展 [J]. 科研信息化技术与应用, 2010, 1: 20-6.
[13]刘婷, 付强. 高性能计算及其在航空发动机中的应用 [J]. 航空动力, 2018, (4): 21-5.
[14]郑晓欢, 陈明奇, 唐川, et al. 全球高性能计算发展态势分析 [J]. 世界科技研究与发展, 2018, 40(3): 249-60.
[15]GRAY J S, HWANG J T, MARTINS J R R A, et al. OpenMDAO: an open-source framework for multidisciplinary design, analysis, and optimization [J]. Structural and Multidisciplinary Optimization, 2019, 59(4): 1075-104.
[16]全栋梁, 时光辉, 关成启, et al. 结构优化技术在高速飞行器上的应用与面临的挑战 [J]. 力学与实践, 2019, 41(4): 343-81.
[17]DASSAULT SYSTèMES INC. ISIGHT & THE SIMULIA EXECUTION ENGINE [Z].
[18]NOESIS SOLUTIONS NV. OPTIMUS IN BRIEF [Z].
[19]R&D INC. Software for Process Integration and Multidiscipline Design Optimization [Z].
[20]PHOENIX INTEGRATION INC. ModelCenter® Integrate increases productivity by enabling users to execute significantly more simulations with less time and resources. [Z].
[21]SANDIA CORPORATION. Dakota Reference Manual Version 6.11 [Z].
[22]MATHWORKS INC. Optimization Toolbox Solve linear, quadratic, integer, and nonlinear optimization problems [Z].
[23]MATHWORKS INC. Statistics and Machine Learning Toolbox Analyze and model data using statistics and machine learning [Z].
[24]SVANBERG K. The method of moving asymptotes- a new method for structural optimization [J]. International journal for numerical methods in engineering, 1987, 24(2): 359-73.
[25]LOPHAVEN S N, NIELSEN H B, SøNDERGAARD J. DACE - A Matlab Kriging Toolbox, Version 2.0 [J/OL] 2002, 2020.02.24]. http://www2.imm.dtu.dk/pubdb/views/edoc_download.php/1460/zip/imm1460.zip.
[26]COUCKUYT I, DHAENE T, DEMEESTER P. ooDACE toolbox: a flexible object-oriented Kriging implementation [J]. The Journal of Machine Learning Research, 2014, 15(1): 3183-6.
[27]MARELLI S, SUDRET B. UQLab: a framework for uncertainty quantification in MATLAB [Z]. Second International Conference on Vulnerability and Risk Analysis and Management (ICVRAM) and the Sixth International Symposium on Uncertainty, Modeling, and Analysis (ISUMA). Liverpool; American Society of Civil Engineers. 2014.10.3929/ethz-a-010238238
[28]BOUHLEL M A, HWANG J T, BARTOLI N, et al. A Python surrogate modeling framework with derivatives [J]. Advances in Engineering Software, 2019, 135: 102662.
[29]周铸, 黄江涛, 高正红, et al. 民用飞机气动外形数值优化设计面临的挑战与展望 [J]. 航空学报, 2019, 40(1): 522370.
[30]ZAKERDOOST H, GHASSEMI H. A multi-level optimization technique based on fuel consumption and energy index in early-stage ship design [J]. Structural and Multidisciplinary Optimization, 2018, 59(5): 1417-38.
[31]金海波, 丁运亮. 飞机概念设计中的外形参数化模型的研究 [J]. 南京航空航天大学学报, 2003, 35(5): 540-4.
[32]颜力, 陈小前, 王振国. 飞行器多学科设计优化中的灵敏度分析方法研究 [J]. 航空计算技术, 2005, 35(1): 1-6.
[33]穆雪峰, 姚卫星, 余雄庆, et al. 多学科设计优化中常用代理模型的研究 [J]. 计算力学学报, 2005, 22(5): 608-12.
[34]肖正懿, 郑荣. 一种多软件联合仿真分析方法 [J]. 机床与液压, 2010, 38(6): 107-9.
[35]赵坚勇, 初鹏, 隋永枫, et al. 基于SiPESC.OPT的透平低压排汽缸优化设计 [J]. 计算机辅助工程, 2013, 22(4): 29-33.
[36]AGTE J, DE WECK O, SOBIESZCZANSKI-SOBIESKI J, et al. MDO: assessment and direction for advancement—an opinion of one international group [J]. Structural and Multidisciplinary Optimization, 2009, 40(1): 17-33.
[37]VAN GENT I, LA ROCCA G, HOOGREEF M F M. CMDOWS: a proposed new standard to store and exchange MDO systems [J]. CEAS Aeronautical Journal, 2018, 9(4): 607-27.
[38]张月玲, 白文. 航空高性能计算和数据处理需求评论 [J]. 航空计算技术, 2009, 39(1): 146-50.
[39]HASTINGS W K. Monte Carlo sampling methods using Markov chains and their applications [J]. Biometrika, 1970, 57(1): 97-109.
[40]LUO Y Z, LIANG L B, WANG H, et al. Quantitative Performance for Spacecraft Rendezvous Trajectory Safety [J]. Journal of Guidance, Control, and Dynamics, 2011, 34(4): 1264-9.
[41]BAE H-R, GRANDHI R V, CANFIELD R A. Uncertainty Quantification of Structural Response Using Evidence Theory [J]. AIAA Journal, 2003, 41(10): 2062-8.
[42]WU J, ZHANG Y, CHEN L, et al. A Chebyshev interval method for nonlinear dynamic systems under uncertainty [J]. Applied Mathematical Modelling, 2013, 37(6): 4578-91.
[43]BAUDIN M, DUTFOY A, IOOSS B, et al. OpenTURNS: An Industrial Software for Uncertainty Quantification in Simulation [M]//GHANEM R, HIGDON D, OWHADI H. Handbook of Uncertainty Quantification. Pasadena; Springer. 2015: 2001-38.
[44]PATELLI E, BROGGI M, ANGELIS M D, et al. OpenCossan: An Efficient Open Tool for Dealing with Epistemic and Aleatory Uncertainties [Z]. Second International Conference on Vulnerability and Risk Analysis and Management (ICVRAM) and the Sixth International Symposium on Uncertainty, Modeling, and Analysis (ISUMA). Liverpool; American Society of Civil Engineers. 2014: 2564-73.10.1061/9780784413609.258
[45]SCHITTKOWSKI K. NLPQL: A fortran subroutine solving constrained nonlinear programming problems [J]. Annals of Operations Research, 1986, 5(2): 485-500.
[46]KELLER A. Monte Carlo and Quasi-Monte Carlo Methods 2012. Springer Proceedings in Mathematics & Statistics [M]//DICK J, KUO F, PETERS G, et al. Quasi-Monte Carlo Image Synthesis in a Nutshell. Berlin; Springer. 2013: 213-49.
The Research and Development Progress of General Multidisciplinary Integrated Optimization Software SiPESC.OPT
Shuai Mei1, Chao Li2, Xueze Lu3, Sinan Yi4, Fengmin Wang5* Biaosong Chen6
(1 Dalian SiPESC Technology Company, Dalian, Liaoning, 116024, China.;
2. College of Materials Science and Engineering, Qingdao University of Science and Technology, Qingdao 266024, China;
3 Department of Engineering Mechanics, Dalian University of Technology, Dalian 116024, China.;
4 Beijing Research Institute of Mechanical &Electrical Technology, Beijing, 100083, China.;
5 Institute of Applied Mathematics, China Aerospace Science and Industry Corporation, Beijing, 100048, China.;
6 Department of Engineering Mechanics, State Key Laboratory of Structural Analysis for Industrial Equipment;
Dalian University of Technology, Dalian, Liaoning, 116024, China.;
* Corresponding author: Fengmin Wang, E-mail: casic_wfm@163.com)
ABSTRACT: SiPESC.OPT is a general multidisciplinary integrated optimization software developed based on the software platform SiPESC and used to solve engineering and scientific decision problems. The previous version of SiPESC.OPT provides a variety of mainstream optimization algorithms library, supports many commonly used methods to create experimental design and surrogate model, and it has been successfully used to solve many engineering problems. This paper introduces the recent research and development progress of SiPESC.OPT. 1) An easy-to-use interactive mode (based on the so called “Filter chart”) is adopted to design the GUI part of software. Based on this mode, the GUI parts for the quick optimization problem definition, optimization task construction, automatic engineering software data reading and writing in parameterization, visualization of optimization result etc. have been developed to improve the operability. 2) The calculation box tool has been developed to provide a variety of software integration tools. In especial, the SSH calculation box provides broader support for optimization with large-scale computation and complex process in remote computer cluster. 3) It added some commonly used methods in optimization, design of experiment, the surrogate model algorithms, including gradient optimization algorithm NLPQLP, multi-objective algorithms NSGA2, optimal Latin square and Sobol in experiment design, the tensor product orthogonal polynomial and sparse regression orthogonal polynomial algorithm in surrogate model algorithms. 4) It also adds quality design functions, including the taguchi experiment design, the Monte-Carlo and JC reliability methods and the six sigma quality reliability optimization design. The functions newly developed above provides a solid foundation for the wider application of SiPESC.OPT
Key words: SiPESC.OPT、drag-and-drop GUI, remote optimization task, NLPQLP optimization solver, Sobol experimental design
CAE年会分论坛事件回顾|11月14日轻质、复合材料及新材料、新工艺数字仿真技术论坛和国防科技工业数字仿真专题论坛-现场回顾
CAE年会分论坛事件回顾|11月14日CAE自主软件开发与应用专题论坛-现场回顾
CAE年会分论坛事件回顾|11月14日汽车及交通运输行业数字仿真专题论坛-精彩现场


