摘要
多物理场耦合问题在存在于多种自然现象及工业问题中，并逐渐成为科技领域的一个重要研究方向。本文对多种常见的多场耦合问题进行讨论，并给出了其控制方程的统一形式。针对多场耦合问题，本文提出了一种新算法：分域自由单元法。该算法是一种强形式算法，无需对问题的控制方程做出额外的处理，可使得多种问题的求解模式得到简化，因此该方法非常适用于处理复杂的多场耦合问题。此外，本文基于加权残数法给出伽辽金形式的分域自由单元法，可以较好的提高算法的精度和稳定性。根据本文提出的强-弱形式的自由单元法，开发出了针对多场耦合问题的数值仿真软件-Freman。该软件具有完备的前后处理功能，清晰地分析逻辑，可以求解多种复杂的物理问题。在本文中，利用Freman软件，并传热、热力耦合、压电智能材料进行分析。
关键字 多场耦合问题、自由单元法、软件开发
中图分类号：O302 文献标识码：A
1. 引言
工业领域中，温度场，应力场，湿度场，电场等都属于物理场。随着科技的发展，人们遇到的问题由单场发展到多物理场耦合问题。这些多场问题中的变量值往往是人们所关心的，如结构的温度、应力、位移等。为了得到现实问题中的应力、位移、温度、电势等物理量，需要对多场耦合问题进行求解。
通过数学形式的表达，单场或者多场耦合问题的表示形式为一系列二阶偏微分方程组(PDEs)。但是其控制方程及模型往往是是非常复杂的，这导致问题的直接求解十分困难。自20世纪40年代以来，人们就一直在致力于利用计算机来求解各种物理现象，同时也发展出了多种数值求解算法。现有的数值算法有差分法[1]，有限体积法[2-3]，有限单元法[4-5]等。差分法为强形式算法，但是其很难解决复杂几何外形的问题。有限元法在固体力学领域拥有着极广泛的应用，有限体积法在流体力学方面有着广泛的应用。但是求解多场耦合问题，现如今还没有一个统一的算法。基于这些算法，国外开发了一些仿真软件，如ANSYS，ABAQUS等。国内的CAE软件有大连理工大学的SiPESC[6]，北京大学的SAP84[7]，中科院的FEPC[8]，重庆励颐拓软件的LiToDesk平台[9]。但是目前多场耦合软件较少。现有的应用广泛的多场耦合软件有Comsol软件，其基于有限元法，可以求解大量的多场耦合问题。
针对多场耦合问题的复杂形式，建立统一的求解算法有利于CAE软件的搭建。近年来，强形式的自由单元法[10]在众多领域中得到了广泛的应用，但是其在多场耦合问题中应用较少。在本文中，针对多场耦合问题，建立求解的统一形式。并在强形式算法的基础上，开发更稳定
基金支持：国家自然科学基金NO.12072064
的弱形式算法。基于强/弱形式的自由单元法，开发了国产CAE软件Freman。Freman可以求解现有的大部分多场耦合问题，如热-力、电-力、流固耦合传热等多种问题。在本文中，给出了基本的多场耦合问题控制方程的统一形式，建立了强弱形式的自由单元法，并基于该算法建立CAE仿真软件，并对传热、热力耦合、压电智能材料进行分析。
2. 多场耦合问题控制方程的统一形式
多场耦合问题的形式多种多样，其常见的有热-力耦合，力-电耦合，热-力-电耦合，热-力-电-磁等。根据问题的不同，其控制方程也不相同。固体中的力学、热学、电、磁学等单场问题的控制方程及边界条件已经被众多学者提出，并可以归纳为二阶偏微分方程的形式。本文给出几个常见问题的控制方程，并根据规律给出多场耦合问题控制方程的统一格式。
2.1 稳态热传导问题
对于给定的计算域及边界,稳态热传导问题的控制方程的一般形式为
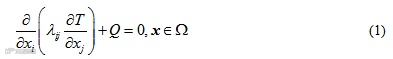
其中
为热导率张量，
为热源，
为温度。该问题的边界条件为
其中
分别为该问题的三种边界条件（Dirichlet, Neumann和Robin边界条件）。
2.2 稳态热-力学问题
稳态热-力学问题的控制方程的一般格式为
其中
为应力张量，
为体积力。应力张量
与应变与温度的关系为
其中，应变张量为
为弹性本构张量
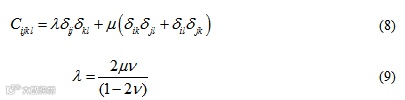
在以上式中，
为剪切模量，
为泊松比。此外，
其中为热膨胀系数。同样的，其边界条件可归纳为以下两类：
2.3 压电问题
压点问题的控制方程为
其中
其中
为弹性本构张量，
为压电常数，
为介电常数。此外，
为电场强度，其与电势的关系为
此外，该问题的边界条件为
2.4 多场耦合问题的统一格式
对于不同的单场及多场耦合问题，其分析的自由度也不相同。为了便于多场耦合分析，现构造跟对于多场耦合问题的统一格式。其统一格式的本构方程为
其中本构张量的格式具体示意图如下：
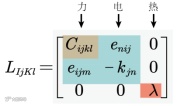
图1. 热-电-力耦合问题的本构张量
则相应的，其控制方程为
其Neumann边界条件为
其中为广义位移。从以上两式中可以看出，复杂的多场耦合问题可以简化为一个统一的控制方程，其形式为一个二阶偏微分方程。
3. 强弱形式的分域自由单元法
使用数值手段求解偏微分方程的第一步是对计算域进行离散。类似于等几何法中的分片(patch)，在本文中需要将计算域划分为互不重叠的子域(sub-domain)或块(block)。不同于等几何中采用样条曲线描述分片信息，在本文中采用有限元中的单元才存储子域的几何信息。对于每个子域，可将其转化为参数空间的规则形状
，并在参数空间中不同方向均匀地布置散点(
)。对于每一个散点，可根据所述子域内的周围散点形成配点单元。具体的子域映射及配点单元形成过程见图2.
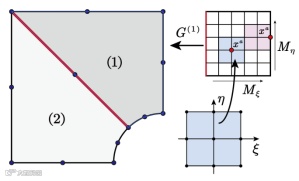
图2. 几何离散、子域坐标变换及局部配点单元的形成
3.1 形函数的构造及导数的计算
从图2中可以发现，节点形成的局部配点单元为拉格朗日单元，因此变量满足拉格朗日插值格式
其中为单元中的节点数目，为拉格朗日插值形函数，其可以根据一维拉格朗日插值进行计算得到。一维问题的拉格朗日插值的具体形式如下
则相应的二维问题的形函数形式为
相似的，三维问题的形函数也可以通过该方式获得。
对于现有的物理问题，其控制方程需要用到变量的一阶导数及二阶导数。形函数对局部坐标的一阶及二阶导数可直接获得。如变量
对局部坐标
的
阶导数为
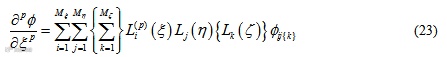
其中大括号中的内容适用于三维问题。
对于几乎所有的物理问题，其计算域通常是不规则的。因此在得到了参数坐标下变量的导数之后，要采用坐标变换技术得到其在全局坐标的导数。考虑计算域内的某连续函数，其一阶导数及二阶导数的具体格式为
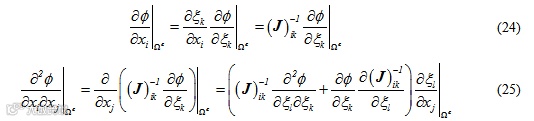
其中
为坐标变换的雅克比矩阵。雅克比矩阵的逆
可通过下式计算
则其关于局部坐标的导数为
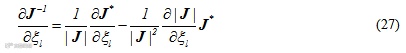
将式及代入式及中，可得变量关于全局坐标的导数：
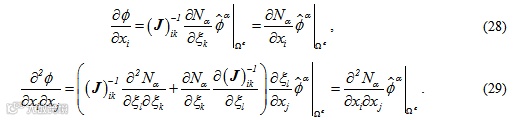
3.2 强形式分域自由单元法
对于现有分析的问题，其控制方程的统一形式为一个二阶偏微分方程，方程中存在着变量对全局坐标的一阶导数及二阶导数。和大部分无网格法相似，变量通过形函数离散之后，直接将形函数关于全局坐标的一阶导数及二阶导数代入控制方程，得到最终的离散格式。
和绝大多数强形式算法相同，对于子域内的节点（内部点），其满足控制方程；对子域的界面点（边界点），其满足通量平衡边界条件。因此可针对不同节点直接建立控制方程。考虑问题为功能梯度问题，则对于内部点，有
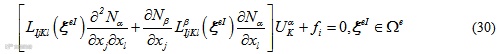
对于子域与子域之间的界面点，有
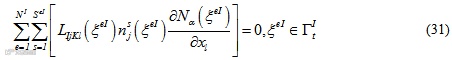
其中为与节点相关联的单元数量，为与节点相连的单元的面数量。
对于计算域的边界点，有
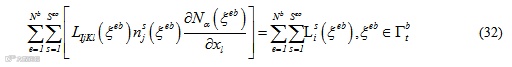
其中
为与节点
相关联的单元数量，
为与节点相连的单元
的面数量，
为面上施加
的通量。根据离散后模型中的节点位置，可对每一个节点建立离散方程
通过求解方程，可得所需节点变量值，如位移，温度，电势。
强形式自由单元法具有形式简单的特点，无需对控制方程做出特殊处理，因此及适用于多场耦合问题。但是由于在形成方程中需要用到二阶导数，因此该算法的精度较低。
3.3 弱形式分域自由单元法
为了提高算法的精度及稳定性，可根据加权残数法，建立Galerkin形式的弱形式自由单元法。根据加权残数法的基本思想，权函数取为形函数。图3给出了两个不同配点的权函数图。
图3. Galerkin自由单元法中不同配置点的权函数
对于多场耦合问题的统一控制方程，其局部弱式为
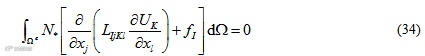
其中为节点*的形函数。考虑到分部积分，可得
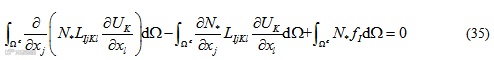
使用高斯散度定理，可得
通过将变量对全局坐标的导数（式）代入上式，得
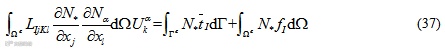
通过上式可得到与式相同的系统方程。通过求解方程可得所需节点变量值，如位移，温度，电势等。
4. 基于分域自由单元法的CAE软件开发
一个高质量的数值仿真软件包括数值计算、数据整理和图形界面这三大模块。在数值计算模块，采用分域的自由单元法，分为强/弱两种不同形式进行计算。在图形界面领域，基于PyQt5设计GUI窗口，并采用VTK进行三维模型显示及后处理。基本的CAE软件框架如图4所示。
图4. CAE平台框架
4.1 基于Qt+VTK的用户图形界面
通过设计图形用户界面(GUI)，用户可以更便捷地使用仿真软件进行计算。考虑到用户群的特点，自由单元法采用跨平台图形界面开发程序Qt的python版本，开发如图5所示的图形用户界面。用户界面参考了大部分现有的商业软件，并针对用户习惯及多场耦合分析顺序做出相应的设计调整。图5中给出了软件的几大窗口，用户可方便的通过GUI对模型进行操作分析。
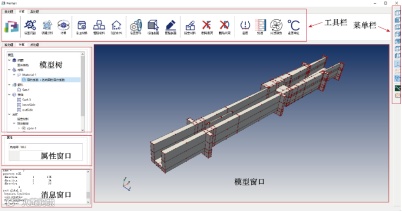
图5. 基于分域自由单元法的用户界面Freman
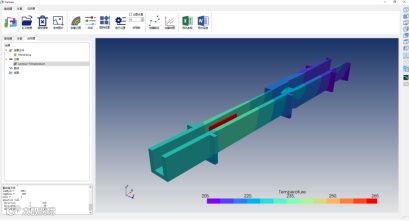
图6. Freman用户界面的后处理功能
4.2 多场耦合问题的软件集成
由第三章建立的多场耦合问题的统一形式，及强/弱形式的自由单元法，可依据问题的不同建立统一的方程进行求解。首先，在用户界面上形成必要信息，如节点、单元、边界条件、材料等输出至文件系统中。同时，调用可独立运行的程序BFREM.exe进行计算吗，所得结果输出至Freman用户界面进行后处理。
5. 一些典型算例
基于分域自由单元法开发的用户界面程序，针对传热问题、热力耦合问题、压电智能材料问题进行分析。
5.1 三维传热问题
在本算例中为一个三维传热分析。该模型的内半径为
，外半径为
，厚度为
，其中有8个圆孔，其半径为
。由于对称性，去模型的1/8分析，其外形图如图7所示。该模型的外边界载荷热流为
，内表面施加温度边界条件
。经过分域之后，设置节点的平均间距为3.0。经过Freman计算所得温度云图如图8所示。
图7. 带孔圆筒的1/8模型及Freman计算所得温度云图（弱形式）
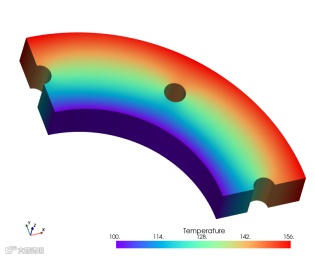
图8. Freman计算所得温度结果云图
更了更精确的比较强形式和弱形式算法的精度，使用同样网格数量的有限元法进行计算并对结果进行比较。有限元法、强形式Freman和弱形式Freman三种算法所得文路径1上的温度云图如图7所示。从图7中可以很显然地看出，弱形式Freman算法具有很高的精度，所得计算结果与有限元法计算所得温度吻合较好。
图9. 不同算法计算所得路径1上节点为温度曲线图
5.2 三维热-固耦合问题
继承于上一个算例，本算例是一个热-固耦合问题，所采用的几何模型为5.1中所使用的模型，温度边条件见5.1节。此外，由于对称性，模型的几个对称面施加对称边界条件，模型的内壁面是在压力载荷为。针对此热-固耦合问题，经过计算，所得的总位移云图和von-mises云图如图10所示。此外，在路径1上比较了与有限元计算所得位移的趋势，如图11所示。从图中可以看出，弱形式算法与FEM计算所得结果吻合较好。
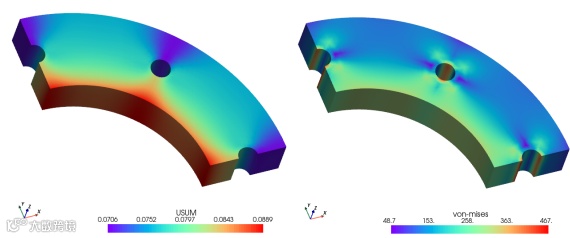
图10. Freman计算所得总位移云图和von-mises应力云图
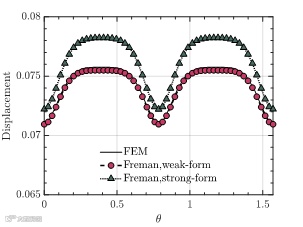
图11. 不同算法计算所得路径1的总位移曲线图
5.3 压电智能材料耦合问题
最后一个算例为某智能压电音叉的力-电耦合分析。其几何外形图及其在Freman中的分域如图12所示。音叉的底部为固定约束，并给定电势为0。在其两端面，给定均布压力为。音叉材料的正交各向同性智能材料，其相关的物理属性值见表1。
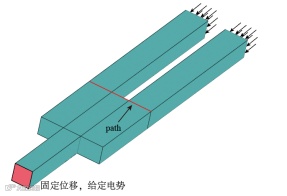
图12. 某压电音叉分域图及边界条件
表1. 正交各向同性压电材料的物理属性
根据Freamn的分域结果，在软件中进行计算。采用的平均网格尺寸为40，分别采用强形式和弱形式两种算法。同时，采用相同网格的有限元进行计算。经过计算，Freman弱形式所得电势云图和总位移云图如图13所示。与此同时，针对三种不同的算法，对指定路径上的节点值进行比较，得到如图14和图15所示的曲线图。从图中可以看出，无论是电势还是位移，弱形式算法所得结果与有限元所得结果十分接近。因此，在以后的分析中，应当使用弱形式进行分析。
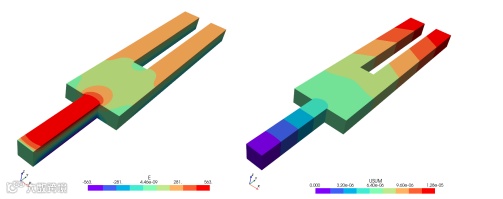
图13. Freman计算所得音叉的电势云图和总位移云图
图14. 三种算法所得指定路径上的电势曲线图
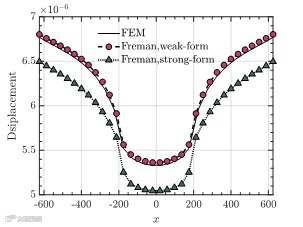
图15. 三种算法所得指定路径上的总位移曲线图
参考文献
[1] P.S. Jensen, Finite difference techniques for variable grids, Comput. Struct. 2 (1972) 17–29.
[2] W.Q. Tao, Y.L. He, Q.W. Wang, Z.G. Qu, F.Q. Song, A unified analysis on enhancing single phase convective heat transfer with field synergy principle, Int. J. Heat Mass Transf. 45 (2002) 4871–4879.
[3] J. Li, G.P. Peterson, P. Cheng, Dynamic characteristics of transient boiling on a square platinum microheater under millisecond pulsed heating, Int. J. Heat Mass Transf. 51 (2008) 273–282.
[4] O.C. Zienkiewicz, R.L. Taylor, The Finite Element Method, McGraw-Hill, London, 1989.
[5] G.R. Liu, S.S. Quek, The Finite Element Method: A Practical Course, Second ed., Butterworth-Heinemann, Oxford, 2013.
[6] 张洪武，陈飙松，李云鹏，等．面向集成化CAE 软件开发的SiPESC研发工作进展．计算机辅助工程，2011,20( 2) : 39-49．
[7] 杨罗宾，袁明武，陈璞，等. 微机结构分析通用程序SAP84(版本4.0)．计算结构力学及其应用，1995，12( 3) : 298-300.
[8] 梁国平，唐菊珍. 有限元分析软件平台FEPG. 计算机辅助工程, 2011, 20(3) : 92-96．
[9] Liu Y , Cheng L , Zeng Q , et al. PCLab - A software with interactive graphical user interface for Monte Carlo and finite element analysis of microstructure-based layered composites. Advances in Engineering Software, 2015, 90(DEC.):53-62.
[10] Gao X.W., Gao L.F., Zhang Y. Free element collocation method: A new method combining advantages of finite element and mesh free methods, Computers and Structures 2019, 215: 10–26.
作者简介
徐兵兵，博士，大连理工大学航空航天学院
主要研究方向为计算力学、多物理场耦合计算、CAE软件开发，在断裂力学，弹塑性力学及智能材料计算方面做了大量工作。此外，在无网格法，边界元法领域有相关研究。