摘 要:工业货架通常在沿巷道方向为无辅助支撑设计以方便货物存取,因而其稳定性主要取决于横梁与立柱挂齿式连接的梁柱节点,冷作硬化效应虽然提高了薄壁型钢材的屈服点但降低了延展性,地震等强冲击过程中梁柱节点常发生脆性断裂或性能退化,有可能引发货架连续性垮塌。本文基于低周反复加载试验,建立了工业货架梁柱节点恢复力仿真模型,以滞回耗能能力为指标对梁柱节点的退化性能进行数值分析。结果表明,节点参数中连接形式对节点的抗震性能影响最为明显,其次是挂片焊接位置、厚度以及安装间隙,为工业货架抗震设计提供参考。
关键词:钢结构货架;梁柱节点;数值分析;性能退化;节点参数
基金项目:上海市工程技术研究中心能力提升计划资助(17DZ2283800)。
0 引言
对比传统钢结构建筑,冷弯型薄壁钢工业货架的载重大多来自托盘货载,立柱多为开孔薄壁截面,为主要承重构件,冷弯型钢材具有较高屈服点但延性较差,梁柱节点多为半刚性挂齿式机械连接,滞回特征表现为强非线性和捏拢滑移特性[1-2]。梁柱节点是货架结构中的关键构件,地震过程中,货架整体结构的破坏多由梁柱节点的脆性断裂或性能退化导致[3],其抗震性能和性能退化后的安全性至关重要。到目前为止,国内外都有学者针对薄壁钢梁柱节点抗震性能展开研究:Bernuzzi,Simoncelli等[4]采用非线性时间历程分析及低周疲劳损伤方法来重现梁柱节点的循环行为,研究其损伤分布及震后的有效承载能力;尹凌峰、唐敢等[5]对带有附加螺栓的新型梁柱节点采用悬臂梁试验方法对其进行了反复加载试验,并考察其失效模式、承载能力以及耗能能力。戴明明,陶忠等[6]对4种冷弯薄壁C型钢桁架梁柱节点进行了低周反复加载试验,分析其节点的滞回特性、承载能力等并对比不同类型节点的耗能能力。
货架结构在遭受地震力作用时,载荷会通过结构振动传递到各个节点上,因此目前广泛用于研究梁柱节点抗震性能的悬臂梁反复加载试验,就是通过在梁柱节点处施加低周反复载荷来模拟地震作用下梁柱节点的受力情况。加载装置通常安装在梁构件上用来施加反复载荷,再通过位移传感器和力传感器记录试验过程中梁柱节点的位移和受力,绘制滞回曲线并提取骨架曲线,进而计算节点的耗能能力,通过位移延性系数等指标来评价梁柱节点的性能退化及损伤情况,进而判断梁柱节点的抗震性能优劣。
由于薄壁钢货架的设计及制造缺乏针对尺寸及形式的统一标准,不同厂家所生产的薄壁钢结构构件型号繁多、节点连接形式多样,各种组合下形成的梁柱节点抗震性能各异,难以对每一种节点逐一进行分析评估。因此本文选取了挂片厚度、挂片间隙、连接形式、摩擦系数等参数,通过控制单一变量的方式分析每种参数改变对节点给抗震性能的影响,进而研究不同类型梁柱节点抗震性能的优劣。
1 梁柱节点低周反复加载试验
梁柱节点是钢结构货架的重要组成部分,主要功能是将立柱与横梁连接为一体,其抗震性能对于货架整体结构动态性能有着很大的影响。其主要部件包括立柱、挂片和横梁等,具体结构如图1所示。采用悬臂梁试验平台进行低周反复加载试验并获取滞回特征曲线是梁柱节点抗震性能研究的基础[7]。
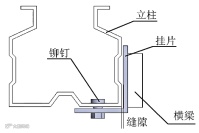

(a)节点连接形式 (b)主要组成部分
图1 梁柱节点典型结构示意图
1.1 试验原理及目的
货架结构在遭遇地震时,梁柱节点可能因结构的振动而承受循环往复的力。本试验的原理就是通过给梁柱节点施加反复加载的静力来模拟节点所遭受的地震力作用,其最终目的是得到梁柱节点的滞回曲线,计算耗能能力,进而提取骨架曲线,计算滞回耗散能力和位移延性系数等指标来评价梁柱节点的退化和损伤特性,图2(a)为测试现场。
1.2 试验过程
试验装置如图2(b)所示,加载点与立柱翼缘表面之间的距离是400毫米[8]。在试验过程中,加载装置预先对横梁施加预载荷,该预载荷是预期失效载荷的10%,然后卸载,负载逐渐增加,直到失效。最后利用数据采集卡记录位移传感器和压力传感器测得的数据,通过计算机的处理,生成M-θ曲线。
1.3 误差修正
由于样件各构件间存在加工精度问题,在装配时可能会导致挂片与立柱间的配合出现误差,悬臂梁一端会因重力而发生下沉,如图2(c);经测算,M100-90系列梁柱节点样件下沉约12mm,M120-100系列样件下沉约3mm。因此在进行数据处理时,将试验1和试验2负向加载时的位移数据减少12mm和3mm,以减少横梁下沉带来的误差。

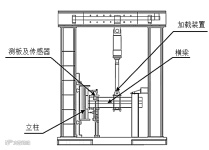

(a)测试现场 (b)装置简图 (c)横梁下沉
图2 反复加载试验
2 恢复力仿真模型及其性能退化指标
由于试验过程较复杂,且考虑到测试成本和计算精度,这里采用建立梁柱节点恢复力仿真模型来分析。根据企业图纸,建立M120、M100型号立柱、B80、B100型号横梁及3爪挂片的三维模型,并将其导入ANSYS Workbench进行有限元分析。
2.1 有限元仿真模型建立
(1)材料设置
梁柱节点组合中各构件的材料参考规范[9]设置,均为Q235钢,弹性模量E为2×1011Pa,泊松比μ为0.3,密度ρ为7850kg/m3,屈服强度为235MPa。
(2)接触设置
横梁与挂片间为焊接,故设置为绑定接触;挂片与三个铆钉之间为绑定,挂片两个内表面与立柱侧面以及铆钉与立柱孔之间均为摩擦接触,其接触行为为完全对称接触,接触方程使用罚刚度法[10]。
(3)网格划分
梁上下两端的加载板采用四边形主导法进行网格划分,模型整体则采用自适应网格划分。四面体和面的最大尺寸设置为5mm,最小尺寸设置为1mm。使用偏斜度检查网格质量,大多数六面体单元的偏度值在0到0.13之间,几乎所有三角形和四面体单元的偏度值都小于0.5,网格质量较好。
(4)约束及荷载设置
约束及荷载的设置也依据试验进行设置,立柱的上下端设置为固定;横梁在套筒及挂片焊接的约束下只可以上下摆动,因此约束横梁Z方向的自由度。作用力的变化参照ANSI MH16.1[11]进行设置,加载点与立柱翼缘表面之间的距离是400毫米,屈服前样件荷载为每级1000N,循环2次;屈服后,样件加载仍为每级1000N,但循环1次。具体设置情况如图3所示。

图3 网格划分及约束设置
2.2 失效模式与滞回曲线
在低周反复加载下,梁柱节点受力及变形情况如图4。观察其应力与应变发现,梁柱节点在受力时铆钉与立柱孔之间挤压现象较明显,由于三个铆钉之间会相互限制转动自由度,未发生明显的铆钉沿立柱孔轴线方向的转动,铆钉外壁与立柱孔内壁之间切线方向相互作用力较小,法向作用力较大。在横梁下压的过程中,挂片上侧与立柱侧壁分离,下侧与立柱侧壁贴合并传递力,三个铆钉对立柱孔的挤压力方向不同,中间孔的所受挤压力较小,上下孔所受的挤压力方向相反,当横梁上抬时,则情况相反。



图4 横梁下压应力云图 图5 滞回曲线图
图5为反复加载下的滞回曲线,该滞回曲线较为饱满,且可以显示出捏拢滑移特性,较符合钢结构梁柱节点的滞回特征。
2.3 仿真模型的验证
(1)破坏形式
对比梁柱节点仿真分析结果与物理试验结果,二者破坏形式大致相同,在循环荷载作用下,立柱孔洞因铆钉的拉压作用而变形,挂片也出现明显变形,如图6所示。

(a)铆钉受拉变形及挂片变形 (b)立柱孔洞豁口
图6 仿真与试验的变形对比
(2)骨架曲线
提取试验及仿真滞回曲线中每个滞回环的顶点,形成骨架曲线,对其进行比较分析,如图7。对比发现,试验结果与仿真结果的骨架曲线基本一致。在循环加载的最后部分,个别点差异较大,原因可能是在试验中梁柱节点中的铆钉会因受力过大而发生松动,而仿真中,由于接触设置,铆钉只会变形,而不会因过度张力与挂片分离。


(a)M100A试验与仿真结果对比 (b)M120A试验与仿真结果对比
图7 试验及仿真骨架曲线对比
通过比较失效形式和骨架曲线的结果,初步验证了梁柱节点仿真分析模型的有效性。因此,可以通过基于试验的有限元分析代替力学试验对梁柱节点的抗震性能进行研究与评估,节省时间和成本,同时也可以获得较为准确的分析结果。
2.4 梁柱节点性能退化指标
(1)滞回曲线和滞回耗能能力
滞回曲线又名恢复力曲线,常用于描述低周反复作用力下荷载和变形之间的非线性映射关系,其中滞回曲线面积代表在循环加载过程中构件消耗的能量,即滞回耗能能力。这里选用Origin软件求取滞回环面积,此软件计算结果精确且操作简单。
(2)位移延性系数
位移延性系数通常定义为极限位移与屈服位移之比,可以使用等能量法通过骨架曲线计算屈服位移Xy,结构的极限位移Xu取为荷载下降至极限荷载85%时的位移,如当骨架曲线无明显下降段时,可取极限载荷所对应位移作为极限位移,其表达式为:
 (2-1)
(2-1)
3 节点参数对性能退化的影响
由于梁柱节点组合形式众多,受篇幅所限,难以对每一种组合的节点都做详尽的分析。因此采用了单一变量的方式,选取了可能影响梁柱节点抗震性能的几个典型参数如:挂片厚度、装配间隙、横梁焊接位置、有无螺栓等如表1所示,对单一参数变化的一系列节点进行分析对比,进而研究每个参数对节点抗震性能的影响大小。
表1 梁柱节点参数设置
模型序号 |
挂片厚度/mm |
间隙/mm |
横梁焊接位置/mm |
有无螺栓 |
摩擦系数 |
A-1(标准) |
4 |
1 |
32(上部) |
无 |
0.15 |
A-2 |
5 |
1 |
32(上部) |
无 |
0.15 |
A-3 |
6 |
1 |
32(上部) |
无 |
0.15 |
B-1(标准) |
4 |
1 |
32(上部) |
无 |
0.15 |
B-2 |
4 |
2 |
32(上部) |
无 |
0.15 |
C-1(标准) |
4 |
1 |
32(上部) |
无 |
0.15 |
C-2 |
4 |
1 |
48(中部) |
无 |
0.15 |
C-3 |
4 |
1 |
64(下部) |
无 |
0.15 |
D-1(标准) |
4 |
1 |
32(上部) |
无 |
0.15 |
D-2 |
4 |
1 |
32(上部) |
有 |
0.15 |
E-1(标准) |
4 |
1 |
32(上部) |
无 |
0.15 |
E-2 |
4 |
1 |
32(上部) |
无 |
0.3 |
E-3 |
4 |
1 |
32(上部) |
无 |
无摩擦 |
E-4 |
4 |
1 |
32(上部) |
无 |
绑定 |
3.1 滞回耗散能力对比
提取滞回曲线最后一环,并利用Origin软件计算曲线面积。差值率是对比标准件增减量的百分比,可以表示参数改变所带来的影响。根据表2中A组数据可知:挂片厚度为4mm与5mm的情况下,耗散能力增幅不大,但6mm厚度下节点耗能能力明显提升;根据B组数据可知:安装间隙增加至2mm时,其耗散能力明显增强;由C组数据可知:横梁相对于挂片焊接位置位于中部时,耗能能力最强,位于上部时最弱;由D组数据可知:有螺栓的节点耗能能力对比无螺栓增加五倍;由E组数据可知:摩擦系数对节点耗能能力影响不大,不同摩擦情况下差值率在5%以内。
综上可得,对滞回耗散能里这一指标作对比可以发现:有无螺栓对耗散能力影响最大,其次是焊接位置、挂片厚度、间隙,最小的是摩擦系数。
3.2 位移延性系数对比
根据式2-1计算可得各个节点的位移延性系数,如表2中所示。分析A组数据可以发现:节点延性系数随挂片厚度的增加而增大,但挂片厚度增加至6mm时,延性系数的变化相比耗散能力变化不明显;由B组数据中发现:当间隙增加至2mm时,延性系数增加幅度很小。由C组数据可知:挂片焊接位于中部时延性系数最大,上部时最小;由D组数据可知:有无螺栓对延性系数影响很大;由E组数据可知:不同的摩擦系数对延性系数影响很小。
综上可得:与滞回耗散能力一样,有无螺栓对节点延性系数影响仍为最大,其次是焊接位置、挂片厚度、间隙,影响最小的参数仍为摩擦系数。
3.3 评价指标的敏感性
根据表2,对比滞回耗散能力与延性系数的差值率发现,二者中各节点参数的变化趋势均相同,其中,除模型A-2外,滞回耗散能力的差值率均比延性系数的差值率高,说明滞回耗能能力对梁柱节点各项参数的改变更为敏感,意味着其在各节点参数下的抗震评价最为保守,可作为抗震性能评价的主要指标。
表2 评价指标数值
参数类型 |
模型序号 |
耗能能力/N*mm |
差值率 |
延性系数 |
差值率 |
挂片厚度 |
A-1(Standard) |
178704 |
/ |
1.92 |
/ |
A-2 |
185944 |
4.05% |
2.08 |
8.33% |
|
A-3 |
478528 |
167.78% |
2.11 |
9.90% |
|
间隙 |
B-1(Standard) |
178704 |
/ |
1.92 |
/ |
B-2 |
267041 |
49.43% |
1.95 |
1.56% |
|
挂片焊接位置 |
C-1(Standard) |
178704 |
/ |
1.92 |
/ |
C-2 |
573444 |
220.89% |
2.01 |
4.69% |
|
C-3 |
373654 |
109.09% |
1.88 |
2.08% |
|
螺栓 |
D-1(Standard) |
178704 |
/ |
1.92 |
/ |
D-2 |
1075088 |
501.60% |
2.41 |
25.52% |
|
摩擦系数 |
E-1(Standard) |
178704 |
/ |
1.92 |
/ |
E-2 |
180392 |
0.94% |
1.93 |
0.52% |
|
E-3 |
176369 |
-2.23% |
1.94 |
1.04% |
4 结论
(1)本文以低周反复加载试验为基础,基于ANSYS Workbench建立梁柱节点恢复力仿真模型进行数值分析。结果表明,梁柱节点在承受反复载荷时,铆钉不会发生沿立柱孔轴线的相对转动,加载于横梁上的力主要通过挂片与立柱侧面的挤压以及铆钉与立柱孔间的法向挤压传递;并通过对比物理试验与仿真验证仿真模型的准确性;
(2)选取耗能能力和位移延性系数作为对梁柱节点退化性能评估的综合指标。研究发现,滞回耗散能力相较于位移延性系数对梁柱节点各个参数的变化更加敏感,因此建议将滞回耗能能力作为梁柱节点抗震性能的一个主要指标。
(3)就梁柱节点参数而言,螺栓式梁柱节点可显著改善节点的退化及损伤性能,其耗能能力比普通铆钉式节点增大五倍以上,挂片的厚度与焊接位置以及安装间隙在不同的指标中均有不同程度的影响,而螺栓与立柱孔间的摩擦接触影响极小,在高层、大跨度钢结构货架的仿真中可采用简单的接触方式替代以节约计算成本。
参考文献
[1] 赵宪忠,戴柳丝,黄兆祺等.钢货架结构研究现状与关键技术[J].工程力学,2019,36(08):1-15.
[2] Liusi Dai,Xianzhong Zhao,Kim J.R. Rasmussen. Cyclic performance of steel storage rack beam-to-upright bolted connections[J]. Journal of Constructional Steel Research,2018,148:
[3] 董立婷. 延性钢框架在低周反复荷载作用下损伤退化滞回性能分析[D]. 青岛理工大学,2013.
[4] Claudio Bernuzzi,Marco Simoncelli. An advanced design procedure for the safe use of steel storage pallet racks in seismic zones[J]. Thin-Walled Structures,2016,109:
[5] Yin L,Tang G,Zhang M,et al. Monotonic and cyclic response of speed-lock connections with bolts in storage racks[J]. Engineering Structures,2016,116:40-55.
[6] 戴明明,陶忠等.冷弯薄壁C型钢桁架梁柱节点抗震性能试验研究[J]. 建筑结构,2018,48(6):46-50.
[7] 成博,武振宇. 组装式钢货架螺栓连接梁柱节点试验[J]. 建筑科学与工程学报,2013,30(03):71-77.
[8] FEM10.2.02. The design of static steel pallet racking[S].
[9] 中华人民共和国住房和城乡建设部.钢结构设计标准:GB 50017-2017[S].北京,中国建筑工业出版社,2017.
[10] Lee H H. Finite element simulations with ANSYS Workbench 18[M]. SDC publications,2018.
[11] ANSI MH16.1:2008. Specification for the design, testing and utilization of industrial steel storage racks[S].
第一作者简介:
黄晨宇 男 壮族 上海市
东华大学机械工程硕士研究生
主要研究方向:仓储装备设计、抗震性能分析、有限元分析方面的研究。


