摘 要:薄壁结构是缓冲吸能的研究热点,其复杂的变形模式和吸能特性息息相关,亟需进一步的研究。为了解薄壁圆管在轴向冲击载荷作用下的吸能特性,首先,基于Alexander理论开展了圆形模式下的压缩折叠分析;然后,通过LS-DYNA有限元软件开展了六种结构的仿真研究,并结合吸能指标和屈曲特征进行了讨论。结果表明:双管双肋板的初始峰值载荷最大,单管双肋板的平均载荷最大且吸能总量最多,单管的初始峰值载荷最小、吸能总量最少、比吸能最高;单管及单管单/双肋板三种结构中圆管的屈曲方式均相同,肋板的作用在于加强了结构的刚性,增强了抗冲击变形能力;单管结构较双管结构变形大,且内外管的屈曲变形相似;双管单/双肋板结构两种工况下肋板的屈曲变形相同,双管单肋板结构内管的上端屈曲属于典型的钻石模式,双管双肋板结构内管的屈曲方式为圆环模式。
关键词:薄壁圆管;紫铜;冲击;吸能;屈曲;肋板;有限元仿真
0引言
随着工业的发展,常见的车辆、地铁、船舶、飞机等交通工具越来越多地采用金属薄壁管件和复合材料管件来设计抗冲击缓冲吸能系统[1-3]。近年来,大学方程式汽车大赛勃勃兴起,赛车前端的吸能器设计随之而蓬勃发展,大量的抗冲击缓冲装置涌现,薄壁圆管是研究最为火热的一种吸能结构[4-6]。
杨喆[7]等在薄壁圆筒冲击屈曲吸能行为的实验与数值模拟研究中指出,Johnson- Cook模型能更好地反映薄壁圆筒的冲击屈曲行为。冯悦[8]等开展了材料应变率效应对2类吸能结构碰撞性能的影响研究,结果表明不同结构有不同的材料应变率效应影响因子。卢露[9]等进行了串联蜂窝吸能和冲击稳定性研究,分析了其失稳现象和高速冲击吸能特性。罗伟铭[10]等通过试验研究了成层式铝蜂窝夹芯结构的冲击响应,得出了不同构型铝蜂窝夹芯结构的冲击吸能特性和变形特点。亓昌[11]等对锥形多胞薄壁管斜向冲击吸能特性做了仿真研究,通过对比能量吸收和冲击峰值来评价薄壁结构的吸能特性。然而,这些材料局限于延展性较差的铝及其合金等结构,在高速冲击下容易分裂。
能量吸收性能好的结构应具有能量转换不可逆、稳定且可重复的变形、变形部分行程长、比吸能高等特点。紫铜作为一种高密度金属材料,高速状态下延展性非常好,常用作射流成型的药型罩[12]。这说明紫铜材料塑性好,容易发生大变形将动能转化为应变能和内能。为此,本文基于LS-DYNA有限元软件,开展了薄壁紫铜圆管在受到高速刚性块冲击时的吸能特性及变形模式分析,从吸能总量、比吸能、初始峰值载荷、平均载荷、变形模式等方面评价了肋板对圆管吸能特性的影响。
1理论分析
1.1吸能指标
吸能总量、比吸能(SEA)、平均载荷()、初始载荷峰值是常用的吸能指标[13],可以对冲击载荷下薄壁圆管的吸能特性进行评估。设冲击过程中圆管的吸能总量为E,则比吸能为
 (1)
(1)
式中,M为变形部分的质量,L为变形部分的长度,ρ为材料密度,s为变形长度L的微元位移,P为瞬时载荷,A为圆管截面积。
1.2变形模式
J.M. Alexander[14]将薄壁圆管的压缩吸能分为弯曲能和膜力能,把压缩变形模式描述为基于塑性铰的弯曲和折皱,其能量耗散计算模型和对应的实验结果如下图1。
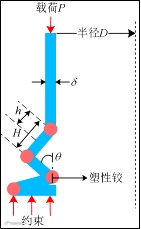
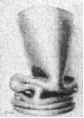
图1 压缩变形模式[14]及实验结果[15]
在这种变形模式下,弯曲能WD计算公式为
 (2)
(2)
式中,M0为每单位圆周长度材料发生压缩产生折皱的力矩,Y为材料单向拉/压的屈服强度。
膜力能Ws计算公式为
 (3)
(3)
根据图1可知,完成一个折皱的角位移θ为π/2,线位移为2H。取平均载荷,将上述公式积分并进行能量平衡有
 (4)
(4)
 (5)
(5)
从而可得
 (6)
(6)
对一个折皱周期(θ=π/2)的平均载荷取极小值,即
 (7)
(7)
因此,折皱的半波长 /Y和平均压溃力为
/Y和平均压溃力为
 (8)
(8)
上式(8)中,壁厚δ通常很小,其平方项更小,故可以略去。对于给定材料,其屈服应力是已知和确定的,此处设为单位1 Pa。取壁厚δ和半径D为自变量,采用Matlab编程对式(8)进行了曲线绘制,结果见图2。由此可以看出,影响产生折皱的主要因素是薄壁圆管的半径、壁厚及材料的屈服应力。
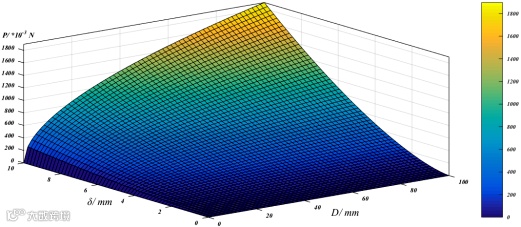
图2 折皱半波长/平均压溃力与圆管半径及壁厚的关系
2仿真分析设置
采用LS-DYNA有限元软件对高速冲击块轴向冲击薄壁圆管的动力学过程进行了仿真。仿真模型包括3个PART(见图3左),即固定的刚性墙PART 1、运动的冲击块PART 3、受压的薄壁圆管PART 2(高90 mm,壁厚2 mm,外径40 mm)。
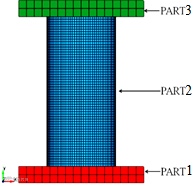
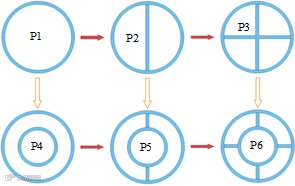
图3 有限元仿真模型及6种仿真工况
刚性墙和冲击块的网格单元采用8节点SOLID 164,材料模型为*MAT_RIGID;薄壁圆管的网格单元采用8节点SHELL 163,材料模型为*MAT_JOHNSON_COOK,约束方程为*EOS_GRUNEISEN。由于研究对象是圆管的受力变形,不关注刚性墙和冲击块的应力应变等信息,因此其网格划分较为稀疏,而薄壁圆管的网格划分则相对较为细致。求解过程中出现的接触采用*CONTACT_AUTOMATIC_SINGLE_SURFACE,动、静摩擦系数均为0.2。为了解决沙漏引起的不规则变形和网格因大变形而引起的不均匀问题,对PART 2设置了沙漏控制(*HOURGLASS)和网格自适应控制(ADAPYIVE MESHING)。冲击块PART 3的初始速度150 m/s,计算时间500 μs。为形成对比分析,仿真工况为(P1)单管、(P2)单管单肋板、(P3)单管双肋板、(P4)双管、(P5)双管单肋板、(P6)双管双肋板,几何模型如图3右所示。
JOHNSON_COOK本构模型的流动应力方程[16]为
 (9)
(9)
式中,A、B、C、n、m为材料参数, 为等效塑性应变,
为等效塑性应变, 为等效塑性应变率,
为等效塑性应变率, 一般取1.0 s-1,
一般取1.0 s-1, 为熔化温度,Tr为室温,Tm为常态下材料的熔化温度。
为熔化温度,Tr为室温,Tm为常态下材料的熔化温度。
EOS_GRUNEISEN压缩和膨胀状态方程[16]为
 (10)
(10)
式中,μ为中间变量,C为冲击波速度-粒子速度曲线的截距,S1、S2、S3为冲击波速度-粒子速度曲线斜率的系数,γ0为GRUNEISEN常数,a是γ0的一阶体积修正量,ρ和ρ0分别为当前密度和初始密度。
刚性墙PART 1、冲击块PART 3均为刚体,材料为Q235钢,薄壁圆筒为紫铜。Q235钢的密度为7.83×103 kg/m3,杨氏模量为210 GPa,泊松比为0.33。紫铜的仿真参数见表1。
表1 紫铜的仿真参数[17]

3仿真结果
3.1吸能特性
通过后处理软件可以得到力-位移关系曲线和冲击块的速度-时间曲线,见图5。从图5中可以得出初始峰值载荷,将曲线求平均值得到平均载荷,载荷曲线与位移围成的面积即是吸能,根据公式(1)即可求得比吸能,各项指标见表2。从冲击力-位移曲线来看,冲击力的初始峰值出现后,来回两个波动后结构便进入稳定的变形区,其位移约为5 mm。稳定变形区即是折皱循环往复产生的阶段。在这个阶段,不含肋板的结构均匀地一圈一圈折皱;含肋板的结构在肋板处出现凸起,这是因为肋板也出现折皱。从冲击吸能指标来看,工况P6的质量最大,初始峰值载荷最大;工况P3的平均载荷最大,吸能总量最多;工况P1的质量最小,初始峰值载荷最小,平均冲击载荷最小,吸能总量最少,比吸能最高。结合运动块速度变化曲线,工况P3的减速效果最好,工况P4也很好。因此,提高结构缓冲吸能的优选方案应该是设置十字形加强肋板和双管。另外,仿真中结构的变形与参考文献[14]和[15]所述的模式及实验结果相同,这证明了本文仿真方法的可靠性。
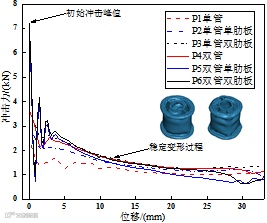

图5 冲击力-位移曲线和运动块速度变化曲线
表2 圆管结构受冲击吸能指标

3.2屈曲特性
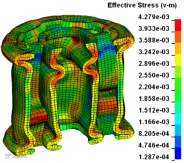
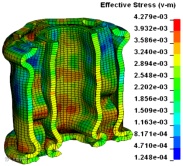
P1~P6等六种工况的有限元仿真结果(等效应力云图及变形)见下图4。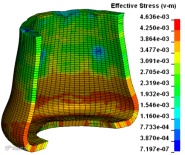


P1 P2 P3
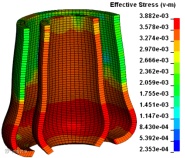
P4 P5 P6
图4 500μs时刻六种工况冲击变形等效应力云图
所有结构底端的材料流动模式或者说变形模式相同,可以采用J.M. Alexander的理论模型加以描述。对比P1、P2、P3三种工况,圆管的变形程度和等效应力峰值依次减小,薄壁圆管的屈曲方式均相同,均为内卷折皱,这说明肋板加强了结构的刚性,提高了结构的抗冲击变形能力。对比P1、P4两种工况,单管结构较双管结构变形大,等效应力峰值也较大,双管结构的内外管屈曲变形相似,这说明双管中内管分担了一些冲击力。对比P4、P5、P6三种工况,很明显地看到双管单和双肋板结构的屈曲方式与双管结构的屈曲方式差别很大,等效应力峰值上升,且应力峰值的分布范围减小。就P5和P6两种工况而言,其等效应力峰值相同,但屈曲方式不尽相同。表现为:双管单肋板结构内管上部出现收缩的皱褶,两半肋板发生S型屈曲,且屈曲方向相反,内管与外管的底部变形模式类似;双管双肋板结构内管的上部未出现收缩的皱褶,而是有发展成圆环褶皱的趋势,其肋板屈曲方式与双管单肋板结构肋板的屈曲方式相同,其内外管的底部变形也与双管单肋板结构内外管的变形方式相同。双管单肋板结构内管上端的屈曲属于典型的钻石模式,而双管双肋板结构内管上端的屈曲属于圆环模式。对于钻石模式,上文中J.M. Alexander的折皱理论解法便不再适用,需进一步更改或修正。在实际的工程问题中,J.M. Alexander理论模型考虑的弯曲能和膜力能是不全面的,还应考虑摩擦能和热能的耗散。
4结论
为研究金属薄壁圆管的冲击吸能及变形特性,建立了Alexander理论模型,并通过有限元仿真对六种工况的薄壁紫铜圆管结构进行了数值模拟,得到如下结论:
(1)对比六种工况的吸能指标,双管双肋板的初始峰值载荷最大,单管双肋板的平均载荷最大且吸能总量最多,单管的比吸能最高,这说明肋板提升结构承载能力的同时也降低了比吸能。
(2)对比双管单和双肋板结构,肋板屈曲变形相同,双管单肋板结构内管上端的屈曲属于典型的钻石模式,而双管双肋板结构的内外管的屈曲方式均为圆环模式,这说明肋板有改变圆管变形模式的作用。
(3)提高结构缓冲吸能的优选方案应该是设置双肋板和形成双管结构,但增加肋板或圆管获得的比吸能并没有成倍地增加,这是设计结构时需要注意的地方。
(4)针对J.M. Alexander理论,推导了圆环模式下折皱发生的临界平均载荷及半波长,并通过Matlab进行了曲面绘制,结果表明半径越大壁厚越大所需的压溃力越大。
参考文献:
[1]张立玲, 高峰. 金属薄壁吸能结构耐撞性研究进展[J]. 金属加工: 热加工, 2006, (1): 76-78.
[2]Zhao C F, Zhou Z T, Ren J, et al. Research on energy-absorption and failure of carbon fiber reinforced epoxy resins double cone structure[J]. Journal of Physics: Conference Series, 2020, 1507: 062006.
[3]Siromani D, Henderson G, Mikita D, et al. An experimental study on the effect of failure trigger mechanisms on the energy absorption capability of CFRP tubes under axial compression[J]. Composites Part A, 2014, 64: 25-35.
[4]夏弋茹. 电动方程式赛车一体式复合材料碰撞缓冲吸能结构研究[D]. 哈尔滨工业大学, 2017, 1-10.
[5]王敏. 轴向压缩下圆管的吸能特性研究[D]. 宁波大学, 2012, 1-20.
[6]赵桂范, 王伟东. 车体结构中圆管撞击吸能特性的有限元研究[J]. 机械科学与技术, 2005, 24(004): 498-501.
[7]杨喆, 魏延鹏, 邹金龙, 等. 薄壁圆筒冲击屈曲吸能行为的实验与数值模拟研究[J]. 兵工学报, 2014, (s2): 244-250.
[8]冯悦, 肖守讷, 朱涛, 等. 材料应变率效应对2类吸能结构碰撞性能的影响[J]. 中南大学学报(自然科学版), 2018, 49(10): 267-277.
[9]卢露, 鲁寨军, 晏明, 等. 串联蜂窝吸能和冲击稳定性研究[J]. 中南大学学报(自然科学版), 2017, 48(7): 1951-1956.
[10]罗伟铭, 石少卿, 廖瑜, 等. 成层式铝蜂窝夹芯结构冲击响应试验研究[J]. 材料导报, 2018, 32(8): 1328-1332.
[11]亓昌, 董方亮, 杨姝, 等. 锥形多胞薄壁管斜向冲击吸能特性仿真研究[J]. 振动与冲击, 2012, 31(24): 102-107.
[12]Zhao C F, Ren J, Kuai T F, et al. Theoretical Analysis of Residual Head Velocity after the Jet Penetrating the Multi-layer Metal-Liquid Composite Structure[C]. IOP Conference Series: Materials Science and Engineering, 2020, 711: 012061.
[13]解江, 宋山山, 宋东方, 等. 复合材料C型柱轴压失效分析的层合壳建模方法[J]. 航空学报, 2019, 40(02): 127-139.
[14]Alexander J M. An approximate analysis of the collapse of thin cylindrical shells under axial loading[J]. Quarterly Journal of Mechanics & Applied Mathematics, 1960(1): 10-15.
[15]徐海斌, 张德志, 谭书舜, 等. 轴向压缩的金属薄壁圆管相似律的实验研究[C]. 第20届全国结构工程学术会议. 2011, NO. CSTAM20ll-E02-0090.
[16]高振宇. 周期胞结构复合装甲抗射流侵彻性能研究[D]. 南京理工大学, 2016, 29-38.
[17]赵昌方, 刘长瑞. 动力黏度对液态复合胞抗射流侵彻影响研究[J]. 兵器材料科学与工程, 2018, 41(06): 88-91.
作者简介:赵昌林(1999.01-),男,白族,贵州毕节人,本科在读,研究兴趣为薄壁结构缓冲吸能及纤维复合材料拉压力学。
第18届中国CAE工程分析技术年会 暨第4届中国数字仿真论坛征文通知(第一轮)


