浅谈引物设计中的Tm值
写在前面的
因为近期自己在进行分子生物学实验相关项目,对于湿实验细节逐步开始有了清晰的认识和理解。上一期推送浅谈自己对PCR引物设计中吉布斯自由能变∆G的认识和理解。初步了解如何预估引物和模板结合能力的强弱。这一次推送将继续记录自己在PCR相关的学习中的有关引物退火温度Tm值感悟和理解。同样,这一次的推送我也将继续参入科学哲学的相关视角或思想。
关于Tm值的背景
根据分子生物学或生物化学教科书中给予的定义Tm值的定义,是两段互补的碱基序列解链50%时的温度。英文中给予的定义也是类似的:The Temperature of Melting (Tm) is defined as the temperature at which 50% of double stranded DNA is changed to single-standard DNA. Tm is basically depends on GC conent. 英文名称解释中特别强调了DNA的Tm值主要依赖于其序列中的GC含量。这主要是因为在碱基互补配对中,A与T配对时形成2个氢键。C与G配对时形成3个氢键。
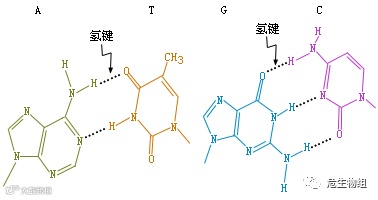
图1.碱基互补配对模式图
如何计算引物的Tm值
事实上,当我学习到Tm值相关知识时,我尝试了解过如何计算Tm值,但看到的一部分资料都回答说用primer5或DNASTAR软件算。很少有从公式概念源头上回答的资料。于是乎,我又开始了一波查阅古老文献。写到这里我不得不吐槽一下,尽管生命科学是一门以实验为主的自然科学,但是这不代表做生命科学研究只需要知道用什么软件计算即可。很多底层生物学问题还是有必要从源头上了解一下的。如果所有东西均是拿来主义,那么生命科学未来发展堪忧。
回到正题上。关于引物的Tm值,目前有超过30种方程可以计算。首先最简单的方程式是
nG/nC/nA/nT: 每种碱基的个数
上面的方程只考虑了引物自身碱基组成对Tm值的影响。根据Tm值的定义,DNA在解链50%时对应的温度。而事实上,当DNA能够达到解链50%的程度时,环境状态如盐离子浓度,DNA自身结构是否对解链有影响呢?如果有影响,那么当DNA解链50%的实际对应温度和用上述方程式估算的温度就存在显著不同。因此,基于这些考虑。研究DNA热力学的科学家在早期就进行了大量理论及实验推导。因此,关于引物Tm值计算的邻近二态模型被提出,引出了第二个公式:
∆H/∆S: 焓变/熵变
R: 摩尔气体常数
C: 寡核苷酸的浓度
常数项: 绝对0度,也叫零开尔文
上述的方程中焓变与熵变都是热力学的状态函数。在前面的吉布斯自由能变的计算中也提及到。在后面的实验中,科学家又发现了体系中Na离子浓度同样影响了DNA解链程度。进一步得出如下公式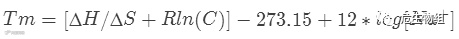
在一般情况下,DNA退火温度的预测由经验数值给出后有如下一种计算方式
Length: DNA长度
当引物的Tm值预测公式给出后,分子生物学家在大量的实验中发现实际的退火温度和预估的Tm值总有一些差异。且这些差异和原来估计的Tm值存在一定关系。因此科学家推测,可以建立一个最佳退火温度的估计模型以通过引物的退火温度确定实际实验的退火温度设定。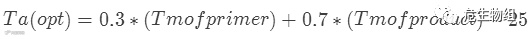
Ta (opt): 预计的最佳实验退火温度
上面的内容仅仅只是关于基于邻近二态模型的Tm计算方法。还有其他不同的计算方法并没有被列出。
不同引物Tm值估计的差异有多大
下面以一段引物5' GCAGCAGCTAGCACTAGCAGCATAG 3'为例子,比较不同计算方法对引物Tm估计的差异。首先利用primer5.0软件预测的Tm值为65.2摄氏度。而选择在线网页使用另外一种计算方式时,Tm值为68.99度。二者相差大约4摄氏度。可以看出,同一个引物在不同软件的预测中Tm值不同(备注:在两个软件的Tm值计算中,我已经将Na离子浓度等其他因素调整为一致的)。

图2.primer5预测的Tm值
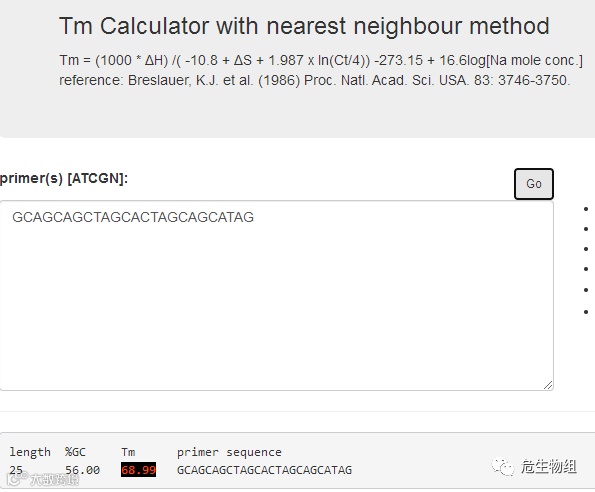
图3.在线网页预测的引物Tm值
写在后面的
从上面的记录可以看出,不同的方法对引物Tm值的预测不同。两种方法谁有谁劣我并不能下一个确定的定论。因为,使用热力学方程预测引物的Tm值只是为实验设计退火温度划定一个合理的范围。实际在实验过程中建议选择梯度优化退火温度。由于关于引物的退火温度预测已经是2000年以前的研究了。随着目前的更新,是否可以利用新的算法。例如统计学习方法甚至是更高级的机器学习模型建立更准确的引物Tm值预测模型呢?
参考文献
Breslauer, K.J., Frank, R., Blocker, H., and Markey, L.A. 1986. Predicting DNA duplex stability from the base sequence. Proc. Natl. Acad. Sci. 83: 3746–3750
Rychlik, W., Spencer, W.J., and Rhoads, R.E. 1990. Optimization of the annealing temperature for DNA amplification in vitro. Nucleic Acids Res. 18: 6409–6412.
联系方式



