本息分摊计算
1、假设年化利率 6%, 月利率则为0.5%;
2、假设贷款金额12万元,贷款期限一年还清,分12期。
错误的算法:利息=12万元 * 6% = 0.72万元 (远远没有这么多)
什么是等额本金,就是每个月的还款中,本金部分相同,利息不同。
期供本金 = Y/n
剩余本金 =(1-k/n)*Y 注:k为第k期,n为总期数
第K期期供金额 = Y/n + (1-(k-1)/n)*Y*i
注:i为利率,按月还为月利率,按年还为年利率。n为总期数,k为已还至k期。Y为总贷款额。
1)每月的本金 = 12万元/12月=1万元 2)每个月的利息
第1月:12 万元 * 0.5% = 600 元 (表示所欠的 12万元在一个月内产生的利息) 第2月:11 万元 * 0.5% = 550 元 (表示所欠的 11万元在一个月内产生的利息) 第...月: 第12月:1 万元 * 0.5% = 50 元 (表示所欠的 1万元在一个月内产生的利息) 利息总计:600+550+500+...+50 = 12*(600+50)/2 = 3900元 (等差数列)
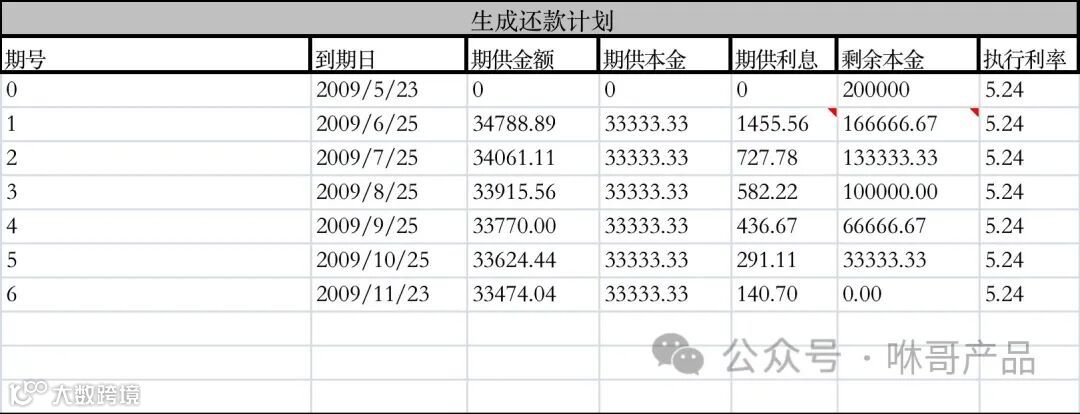
例如:2009-5-23放款200000、年利率5.24%、扣款日25号、6期、等额本金;
就是因为算利息时是按“剩余本金”多少来计算的,因为每个月都还本金,所以剩余本金越来越少,所以利息就越来越少。
什么是等额本息,就是每个月的还款中,本金+利息之和是相同的。
期供金额= 本金*月利率×(1+月利率)^n(期数)/((1+月利率)^n-1);
特点:
在利率不变情况下,借款人每期(月)还款额均相等(即At =A),每期还款额可拆分为本金和利息,但每期本金和利息所占比例都在发生变化,本金所占份额逐渐上升,利息所占份额逐期下降。
设欠款a0,a1,a2,...,a12(=0) a0,表示最初欠款金额,即12万元 a1,表示还第1个月后的欠款金额 a2,表示还第2个月后的欠款金额 … a12,表示还第12个月后的欠款金额,即0元;
每月还款 A(本金+利息)
a0 = 12万元;
a1 = a0(1+0.5%)- A (该公式的含义:a1还欠金额等于 a0加上a0产生的利息(a0*0.5%)再减去A,就是第1月还完后还欠的金额 )
a2 = a1(1+0.5%)- A (该公式的含义:a2还欠金额等于 a1加上a1产生的利息(a1*0.5%)再减去A,就是第2月还完后还欠的金额 )
a3 = a2(1+0.5%)- A …
a12 = a11(1+0.5%)- A(该公式的含义:a12还欠金额等于 a11加上a11产生的利息(a11*0.5%)再减去A,就是第12月还完后还欠的金额, 该金额为 0 ) 按贷款12万,12期还完来计算,最终这个A为10328元,即328元*12月 = 3936元。
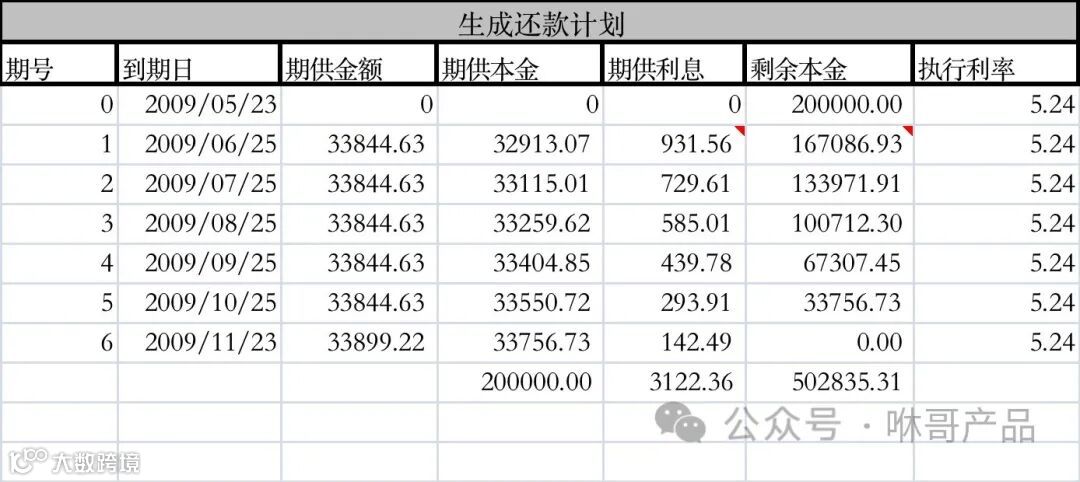
例如:2009-5-23放款200000、年利率5.24%、扣款日25号、6期、等额本息还款计划 (按期+天算)
期供金额:
200000*5.24%/1200*(1+5.24%/1200)^6/((1+5.24%/1200)^6-1)=33844.63;
总结: 提前还款,因为把本金部分都还了,所以后边的利息不用再还,所以不会吃亏的。