

氢原子的超精细结构

邃瞳科学云

2023-09-26

导读：让我们看一个最简单两粒子系统，氢原子由一个质子和一个电子组成，都是自旋为1/2费米子。电子有两个自旋状态，质

让我们看一个最简单两粒子系统，氢原子由一个质子和一个电子组成，都是自旋为1/2费米子。电子有两个自旋状态，质子有两个自旋状态，因此考虑到他们的组合，共有四种组合，即

。两个态矢相乘可以用矩阵的外积来计算，两个二维态矢空间相乘得到四维的矢量空间。

这4个量子态是完备的，根据态叠加原理可以利用4个态作为基础态表达任意波函数：

体系的哈密顿量：

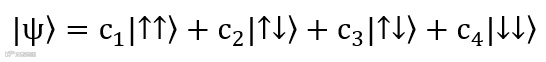
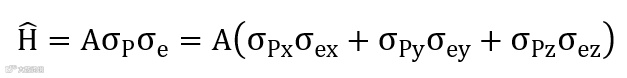
其中，A相互作用强度，而两个泡利矩阵的乘积在这里也是矩阵外积。

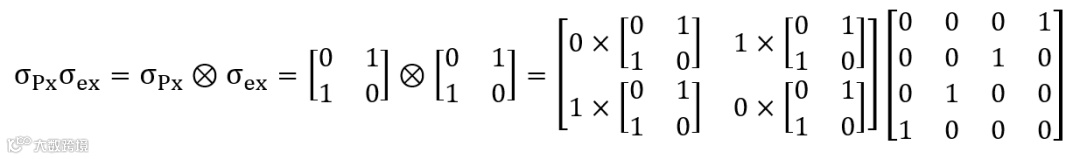
同理可以得到

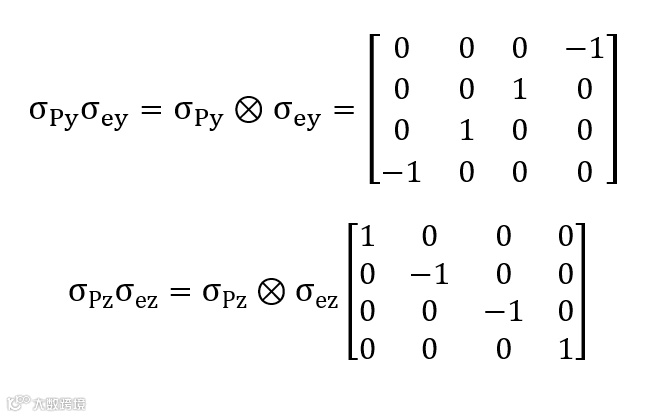
因此体系的哈密顿矩阵

由定态薛定谔方程，可得

解这个线性方程组得到可以得到系统的能谱，由图可知两个能级之间能量差为4A，上能级是三重兼并的，下能级是单态。

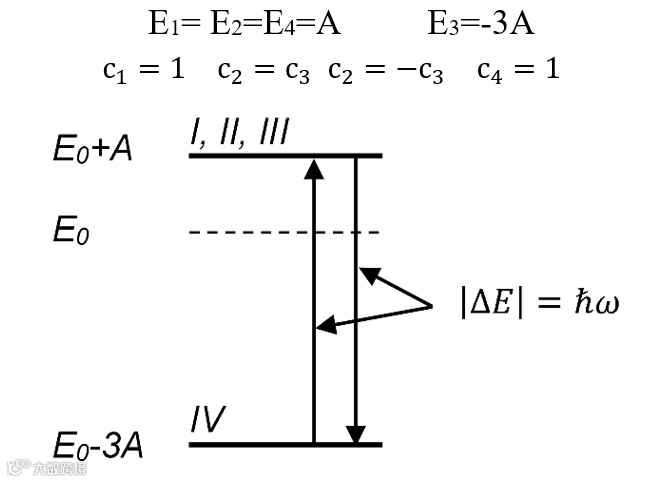
图1 氢原子的超精细结构能级图

由哈密顿量的形式可知，除了对角线上的元素，还有非对角元。这就表明我们最初选择的基态不是定态。实质上这也是质子和电子自旋相互作用的结果。他们各自的自旋都不是守恒量而总自旋才是守恒量

由于下面的例题可知总的自旋角动量取值为1或0，对于总角动量为1的态其磁量子数可以取-1, 0，1。因此按照磁量子数分类应该有四个本征态、和，由上面求得系数，并根据归一化的要求，可以写出这组本征态和我们最初选定的基态之间的关系

两能级之间能量差为4A，与电磁波相互作用的共振频率为

。这个哈密顿量中系数可以通过量子电动力学进行计算，也可通过实验精确的测量。这一共振频率所对应电磁波长为21 cm波，属微波波段。21 cm波在天文学上具有重要的价值，现代射电天文学是从观测这条谱线开始的。1951年，扬·奥尔特（Jan Hendrik Oort）和合作者探测到了中性氢的21厘米波，这个发现在射电天文学上具有里程碑式的意义，奥尔特很快认识到它在研究银河系结构方面的潜力。1958年-1959年，奥尔特等人又绘制出人类第一幅银河系的中性氢21厘米波分布图，证实了银河系的漩涡结构。