薛定谔建立量子力学的基本方程后，需要验证他所猜测的方程是否合理，首先想到就是能否解出氢原子的光谱系，这也是学以致用的典范。但当他把氢原子中电子的哈密顿量和薛定谔方程写出后发现，发现自己并不会解这个方程，于是他就求助于数学物理学家外尔(Hermann Wey, 1885-1955)，在外尔帮助下很快就解出了氢原子的谱线并与实验数据吻合。
氢原子是最简单原子，有一个质子和一个电子组成。对于氢原子模型，简化为电子绕质子的运动，质子仅提供一个静电势能，写出其定态薛定谔方程
由于电子在球形势场中运动，因此利用球坐标解此类问题自然的。球坐标下：
氢原子球坐标下方程
由此可见ψ是r、θ、φ的函数，可以利用分离变量的方法将函数分为径向函数和球谐函数。即
其中是R(r)径向函数， Y(θ,φ)是球谐函数
氢原子方程变为
对于球谐函数
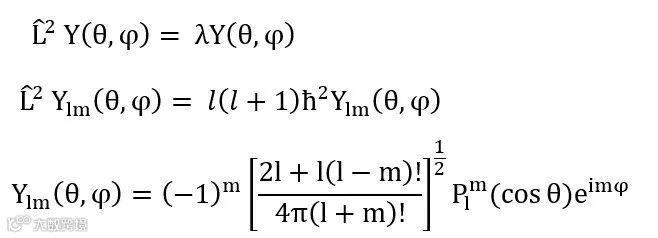
-连带勒让德函数，对 Y(θ,φ)的求解，会得出两个量子数l,m分别称为轨道量子数和磁量子数。
l ≥0 只能取正整数 l = 0,1,2,...,n-1
m 只能取-l ≤ m ≤ l
解径向方程，可以得到系统的主能量
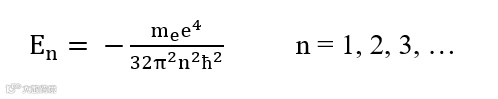
薛定谔在其原文中写道：这些整数出现时，会以振动弦的节点数的相同的自然方式出现，这解释量子力学的本质。
轨道量子数确定绕核转动的角动量
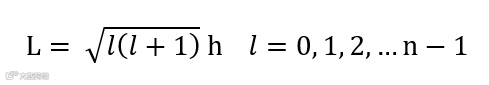
若外磁场沿某一方向，则角动量在空间取向也是量子化的，角动量在外场方向投影大小为
对于玻尔和索末菲人为引入的三个量子数n,l,m，现在这三个量子数是薛定谔方程自然而然解，而且具有明确的联系。在不考虑精细结构和超精细结构的情况下，光谱能量由主量子数和轨道量子数(n, l)决定。对应轨道量子数l=0, 1, 2, 3的亚能级，是由光谱线的特征命名的，以此命名为s, p, d, f轨道(对应于德语Sch äf, prinzipiell, diffuse, fundmental的首字母)。对于 n=1,l=0 表示的是1s能级，也就是基态；对于 n=2 轨道量子数存在两个取值 l=0，1，(2, 0) 对应于2s能级，(2, 1)对应于2p能级 ，相应的还有3d、4f等能级。
致谢：感谢北京工业大学应用数理学院刘鑫教授的十分有益的讨论与指导！
声明
“邃瞳科学云”直播服务
扫描二维码下载
邃瞳科学云APP
