点击 蘑菇云创造 关注我们
第十一课 冰淇淋销量预测
写在前面
Hello,大家好,《Python编程入门系列课程》目前已连更了11课时(共12课时),即将完结。非常感谢一直在关注和学习该系列教程的老师、同学们。
希望大家在学习的同时,也多多为该系列课程提出宝贵建议,我们定当对大家提出的意见和想法进行仔细评估和采纳,后续将继续为大家提供更多系统化的教程和优质的课程~
动动小手扫码,说出您的想法哈

扫一扫
一、学习背景
经过上节课的学习,我们了解了数据处理的一般过程,也学习了数据采集和数据整理。本节课,我们依旧将结合python对数据进行处理与分析,来解决生活中的一些实际问题。
二、学习目标
本实践项目通过编写python程序来预测在一定温度下店铺冰淇淋的销量。
知识目标:
1、理解数据分析
2、掌握回归分析法
技能目标:
1、掌握利用软件工具对数据进行处理的方法
三、学习准备
1、电脑
2、mind+编程软件
核心概念
1)数据分析
数据分析是指用适当的计算方法与工具对收集来的数据进行处理,提取有用信息,形成结论从而支持决策。数据分析可以分为描述性分析、诊断性分析、预测性分析、指导性分析。
2)回归分析法
回归分析法是预测性分析的一种,主要用于比较那些通过不同计量测得的变量之间的相互影响,如价格变动与促销活动数量之间的联系。这些益处有利于市场研究人员,数据分析人员以及数据科学家排除和衡量出一组最佳的变量,用以构建预测模型。
3)回归与回归算法
回归是一种由果索因的过程,即由大量事实所呈现的状态,设法去推断其原因。回归算法一般用于确定两种或两种以上变量之间的定量关系。
例如,在物理实验中,探究小车随时间变化规律这个任务就能通过回归来解决。


在这个实验中,我们依据给出的数据表格,在Excel表格工具中绘制了一副散点图,并添加了一条趋势线来观察这些点的分布特点。
从图中我们可以看到速度和时间的关系表达式为y=2.48x+0.38,R平方值表示线性趋势线对数据拟合的程度,R平方值的值越接近1,代表图像越趋近于真实情况,预测效果越好。那么我们生成这样一个图表的目的是什么呢?
这个实验中探究的是速度和时间的两个变量之间的定量关系,确定此关系后,可以根据需要推测出时间为某一个数值时的速度大小。这种找趋势的方式,也称之为拟合。
拟合是一种数据处理的方式,简单地说就是你有一组数据,觉得这组数据和一个已知的函数(这个函数的参数未定)很相似,为了得到最能表示这组数据特征的这个函数,通过拟合这种方式(具体的数学方法很多)求得函数。而回归是一种特定的数学方法,它可以实现数据拟合,得到函数的参数。当然也有些拟合得到的参数并非是函数的参数,如神经网络,得到的是这个神经网络的参数,这里我们不作深入探究。
四、学习实践
想一想 在炎热的夏季,很多同学都喜欢吃冰淇淋来解暑降温。这也导致了学校店铺的冰激凌往往供不应求。为了能了解所需冰淇淋的数量继而进货满足同学们的需求,店铺老板决定依据过去一年的历史销售数据,来预测在指定温度下冰淇淋的销量。 假如老板把这个任务交给了你,你会怎么做呢?
|
在本项目中,我们将分两步,来预测在指定温度下冰淇淋的销量。
1、探究温度对冰淇淋销量的影响。
2、预测在指定温度下,冰淇淋的销售量。
任务1:探究温度对冰淇淋销量的影响
在这个任务中,我们将探究温度对冰淇淋销量的影响。通过它,我们可以了解数据分析常用的方法。为此,我们将分三步进行探究。首先是采集并整理数据,之后以图表形式将数据可视化出来,最后观察图表并分析数据得出结论。
1、数据采集与整理
在这个项目中,我们从店铺老板处获取记录的数据,数据内容包括日期,气温以及当日的销量等,稍做检查后将数据保存在csv表格文件中。(数据文件见附录1)
2、数据可视化
为了便于对数据进行读取和分析,我们通过编写程序将采集整理好的数据以图表形式呈现出来。
这里我们将采用顺序结构的方式编写程序。具体流程如下:
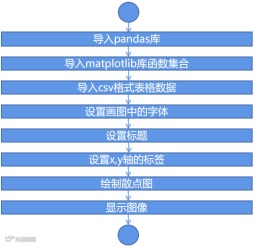
在正式编写程序代码之前,我们首先要创建一个项目文件及python程序文件,并导入表格文件,导入表格的方法与导入gif图相同。
STEP1:创建与保存项目文件
启动Mind+,另存项目并命名为“冰淇淋店销量预测”。
STEP2:创建与保存python文件
创建一个python程序文件“任务一.py”,双击打开。
STEP3:导入数据文件(见附录1)


STEP4:编写程序
import pandas as pd#导入pandas库并用pd来表示
import matplotlib.pyplot as plt#导入matplotlib库中的函数集合
icecream = pd.read_csv("icecream.csv")#导入csv格式表格数据
plt.rcParams['font.sans-serif'] = ['SimHei']#绘制中文字体
plt.title("冰淇淋销量与气温图")#绘制图像标题
plt.xlabel("气温")#绘制x轴标签
plt.ylabel("销售量")#绘制y轴标签
plt.scatter(icecream.iloc[:,1],icecream.iloc[:,0])#绘制散点图
plt.show()#显示图像
STEP5:运行程序
运行程序,我们看到:数据以散点图的形式呈现了出来,图上,横轴表示气温,纵轴表示销售量,一个个蓝色的小圆点表示的就是不同气温下的销售量。

3、数据分析
观察生成的散点图,我们可以发现,整体上,气温对销售量有较大的影响,且气温越高销售量越大。
任务2:预测在指定温度下,冰淇淋的销售量
由上个任务我们已经粗略得知销售量会随着气温的升高而增加,在这个任务中,我们将结合回归分析法,进一步探究销售量与气温间的线性关系,继而预测在指定温度下,冰淇淋的销售量。由于这里用到的数据不变,因此接下来我们只需两步,先通过编写程序得到散点图的线函数关系式,再分析数据进行预测。
1、数据可视化
这里我们将采用顺序结构的方式编写程序。具体流程如下:

STEP1:创建与保存python文件
创建一个python程序文件“任务二.py”,双击打开。
STEP2:安装sklearn库
(1)点击库管理
(2)安装sklearn库
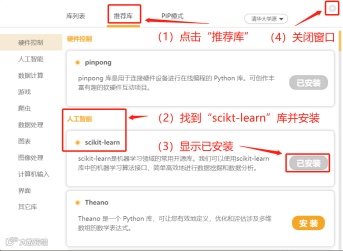
STEP3:编写程序
STEP4:运行程序
(1)运行程序,我们看到,在原有的散点图上,绘制出了一条直线

(2)关闭图表,观察终端,显示了直线的斜率和截距

2、数据分析
通过得到的斜率与截距,我们得出散点图中的线函数式为y=5.2X+57.2。
因而,当气温为25度时,预测的冰淇淋销售量为5.2*25+57.2=187.52,约188个。
当气温为35度时,预测的冰淇淋销售量为5.2*35+57.2=239.2,约239个。
sklearn链接 Sklearn (全称 Scikit-Learn) 是基于 Python 语言的机器学习工具。它建立在 NumPy, SciPy, Pandas 和 Matplotlib 之上,在 Sklearn 里面有六大任务模块:分别是分类、回归、聚类、降维、模型选择和预处理,这里我们简单了解即可。 |
LinearRegression()函数 功能说明 用来实例化线性回归模型。 使用方法 model = LinearRegression() 举例说明 程序中, model = LinearRegression()#实例化线性回归模型,生成model模型对象 表示实例化线性回归模型,生成model模型对象。 |
fit()方法 功能说明 表示以给定数量的轮次(数据集上的迭代)训练模型。这里的“训练”指的是添加数据到模型中,为后续预测作准备。 使用方法 模型对象.fit(x,y,可选参数),这里的可选参数有很多,我们不作一一介绍了。 举例说明 程序中, feature_cols = ['气温']#获取气温列表 x = icecream[feature_cols]#设置x为csv表格中的气温列表 y = icecream.销售量#设置y为csv表格中的销售量 model = LinearRegression()#实例化线性回归模型,生成model模型对象 model.fit(x,y)#训练并存储模型 表示以表格中的气温列表为x,销售量为y来训练模型。
|
predict()方法 功能说明 表示为输入样本生成输出预测 使用方法 模型对象.predict(x,可选参数),这里的x指输入数据,可选参数有很多,不做一一介绍了 举例说明 程序中, plt.plot(icecream.气温, model.predict(x) , color='blue')#绘制直线 这里的“model.predict(x)”就是以x为输入数据,输出预测值。 |
Matplotlib链接 |
plot()函数 功能说明 plot()函数能绘制点和线 使用方法 matplotlib.pyplot.plot(x,y, 参数),其中可选参数有很多,这里我们不一一介绍了 举例说明 程序中, plt.plot(icecream.气温, model.predict(x) , color='blue')#绘制直线 表示绘制一条直线(一次函数),其中,x轴为表格中的气温,y为预测值,直线的颜色为蓝色。 |
五、巩固提高
项目回顾
本节课我们首先探究了温度对冰淇淋销量的影响,利用pandas、matplotlib和sklearn库将数据以图表形式呈现出来,并找到了其中的线性关系,之后通过线性关系式预测了在指定温度下冰淇淋的销售量。
知识小结
1、数据分析的理念
2、回归分析法
附录
附录1表格链接
链接:https://pan.baidu.com/s/102FG0v8s7hGOytex_4uawg
提取码:yc82
附录2
拓展阅读 数据分析工具 计算机数据分析工具目前大致可以分为如下几类:基础类,如简单易用的电子表格软件;统计类,需 要统计学专业知识的分析软件,如SPSS、SAS等;编程类,需要掌握编程知识,如python语言、R语言等;在线类,即在线数据分析平台,如腾讯大数据、阿里云、BDP和AWS等;专业类,多用于大数据分析,如Hadoop,Spark和Storm等。
|
||||||||||||
拓展阅读 数据分析方法 常见的数据分析方法有结构分析法、平均分析法、对比分析法等。 结构分析法是将各个部分与总体进行对比,是分析事物内部的结构、部分与整体之间关系的方法。基本表现形式就是计算结构指标,即各个部分相对于总体所占的百分比。 平均分析法指运用计算平均数的方法来反应总体在一定时间、地点、条件下某一数量特征的一般水平。平均指标中最常用的是算术平均数。 对比分析法指将两个或两个以上的数据进行比较,分析他们之间的差异,揭示出这些数据所反映的事物规律。
|
||||||||||||
拓展阅读 回归的由来 回归”是由英国著名生物学家兼统计学家高尔顿(Francis Galton,1822~1911.生物学家达尔文的表弟)在研究人类遗传问题时提出来的。 为了研究父代与子代身高的关系,高尔顿搜集了1078对父亲及其儿子的身高数据。他发现这些数据的散点图大致呈直线状态,也就是说,总的趋势是父亲的身高增加时,儿子的身高也倾向于增加。 但是,高尔顿对试验数据进行了深入的分析,发现了一个很有趣的现象——回归效应。因为当父亲高于平均身高时,他们的儿子身高比他更高的概率要小于比他更矮的概率;父亲矮于平均身高时,他们的儿子身高比他更矮的概率要小于比他更高的概率。它反映了一个规律,即这两种身高父亲的儿子的身高,有向他们父辈的平均身高回归的趋势。 对于这个一般结论的解释是:大自然具有一种约束力,使人类身高的分布相对稳定而不产生两极分化,这就是所谓的回归效应。
|
||||||||||||
拓展阅读 回归问题的种类 回归算法按自变量的数量划分可以分为:一元回归问题和多元回归问题。
多元线性回归的基本原理和基本计算过程与一元线性回归相同,但由于自变量个数多,计算相当麻烦,一般在实际中应用时都要借助统计软件。
按自变量和因变量之间的关系类型划分可以分为:线性回归和非线性回归。当因变量和自变量之间的关系类似于一次函数时,则属于线性回归,如果类似于指数函数或对数函数,则属于非线性回归。
|



推荐阅读:
文末点击 “ 阅读原文 ” ,下载附件。








