振动的基本概念
v单自由度振动
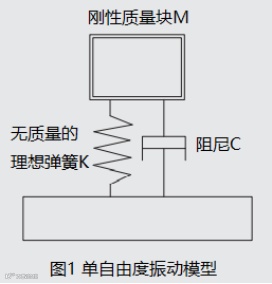
自由振动是振动系统在无外力作用下的振动形式。单自由度振动模型是最简单的振动模型。为了研究方便,把振动系统简化为3个参量进行研究:振动系统由质量M、无质量的理想弹簧K和无质量的阻尼C组成,位于完全刚性的基础之上,M只能在垂直方向上运动,其模型如图所示。
该振动系统的微分运动方程为:

(1)其解为
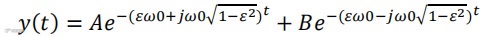
(2)ε为阻尼比C/Cc(阻尼/临界阻尼),ω0为系统固有频率,A/B为振动系统初始条件有关的常数。
v固有频率
解式(2)中,固有频率ω0是振动系统的一个重要参量,它是指振动的刚体离开平衡位置后自由振动的频率,每个振动系统在每个自由度上都有一个固有频率。振动系统的固有频率与振动刚体的质量M和弹簧刚度K有关,单自由度自由振动的固有频率为:

(3)若已知振动系统的静态下沉度,即刚体压在弹簧上后弹簧的压缩量,则系统的固有频率为:

(4)δ为弹簧静态下沉度,m。
v阻尼的效应
解式(2)说明阻尼比对振动系统的运动状态有非常重要的影响:
-ε=0,即无阻尼时,解式(2)变为
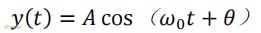
(5)A:初始条件确定的最大位移;
θ:初始条件确定的最大初始相位角。
即此时系统振动不受任何阻力作用,一旦受某一初始力作用后,将以恒定的振幅做简谐振动。
-ε<1,即系统阻尼小于临界阻尼,解式(2)变为

(6)式(6)说明,阻尼越大或系统固有频率越高,则振动衰减越快,振幅随时间的衰减如图2所示。
-ε=1,即系统阻尼等于临界阻尼,解式(2)变为

(7)则振动系统无法形成周期性振动,而是以指数规律恢复到平衡位置,振幅与时间关系如图3所示。
-ε>1,即系统阻尼大于临界阻尼称为过阻尼,解式(2)变为

(8)此时振动系统也无法形成周期性振动,振幅呈指数衰减,如图4所示。



