
极市导读
随机微分方程(SDE)第二篇出炉!本文将聚焦于采样过程,附有相关代码详解。 >>加入极市CV技术交流群,走在计算机视觉的最前沿
前情回顾
上一篇内容主要围绕 SDE 对图像生成任务的建模过程,同时分析了为何 分数模型(SMLD) 和 扩散模型(DDPM) 实质上是两种 SDE 的数值离散形式。在吹水的同时,CW 也相应在每部分给出对应的代码实现,最后还浅浅地训了个 toy demo 作为娱乐项目。
这篇文章将聚焦于采样过程,采样生成样本可谓是生成模型的天职,也是它们最重要的功能(没有之一)。所以,各位友友们都打起精神来吧~!

ps: 本文介绍的采样方法对应 paper 中附录 D~G 的内容,但并非按 paper 中的顺序来介绍。
主角:Reverse Diffusion Sampling
在这篇 paper 所提出的众多采样方法中,处于主角地位的当然非逆向 SDE(reverse-time SDE) 莫属,毕竟作者所讲的故事主题就是 SDE 嘛~ 在上一篇文章中,CW 已经为大家介绍过逆向 SDE 的形式为:

然而在实际进行采样时,我们需要以一个 “可实现” 的时间间隔 去模拟以上那个无穷小的时间微元 。若按1个单位的时间步( i.e. )对以上 reverse-time SDE 实施离散化,就会得到以下形式:

这是将 代入(注意逆向 SDE 的时间微元是负值),同时将等式左边的 离散化为 并移项所得的结果; 是模型在对应时间步所估计的 score; 至于标准高斯噪声 的出现,则是标准布朗运动 变为离散形式的结果。
作者将基于上式这个迭代规则来进行采样的方法命名为 "reverse diffusion sampler"。
为 VE SDE 服务
现在,我们一起来将 reverse diffusion sampling 方法应用于 VE SDE 已知 VE SDE 的表达式为: ,其漂移和扩散系数分别是: ,代入 (i) 式中,就会得到:

第一个等式对导数使用了离散形式,以上就是 reverse diffusion sampler 为 VE SDE 服务的结果。
为 VP SDE 效劳
同理,对于 VP SDE: ,其扩散和漂移系数分别是: ,代入 (i) 式后得到:

可是在论文中,CW 却发现作者针对 VP SDE 所给出的结果是长以下这样的:
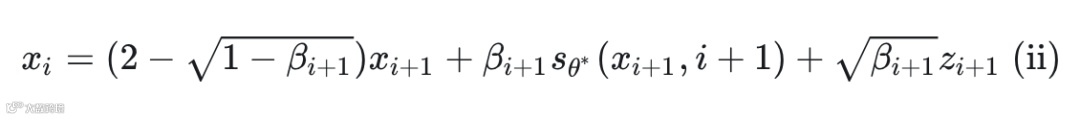
不难发现,等式右边除第一项以外,其余部分和我们的结果长得一模一样,所以我们只需盯住第一项来进行分析即可(教员告诉我们要学会抓住主要矛盾)。

各位友友们要先明确一个非常重要的点,那就是因为这个迭代规则是离散形式的,所以这里的 是 而非 ,也就是说它又变回了 DDPM 所使用的离散的 ,而非 VP SDE 中连续的 。但由于迭代步数 还是同样被假设为很大以至于无穷大,因此 DDPM 的 就会变得很小以至趋于 0 (这样 才能够保持为有限值) ,这就说明上式隐含着 这个条件。

现在,就让我们以 作为前提条件来进一步分析。
不妨来看作者给出的形式: ,可以将其看作是函数 , 忍不住对其进行泰勒展开 (不知道为何,凭直觉很想这样做,可能是各种 paper 的推导过程看多了形成了惯性..),于是:
再将 代入以还原,咦! 惊喜地发现:

另外,作者在论文附录 E 的最后部分还证明了 DDPM 的采样迭代规则祖先采样(https//www.cse.psu.edu/~rtc12/CSE586/lectures/samplingPart1.pdf):

在

General Numerical Solvers
reverse diffusion sampler 是 reverse-time SDE 采用单位时间步 进行离散化的产物。其实,市面上那些网红款数值求解器(solver)均可作用于 reverse-time SDE,最抛头露面当属 Euler-Maruyama(欧拉-丸山)(https//appliedprobability.blog/2020/10/11/euler-maruyama/) 和 Runge-Kutta(龙哥库塔)(https//math.libretexts.org/Courses/Monroe_Community_College/MTH_225_Differential_Equations/03%253A_Numerical_Methods/3.03%253A_The_Runge-Kutta_Method)。在不同 solver 的作用下,就可对应形成不同的采样方法(你要是愿意,可以分别给它们命名),其实也就是 的各种不同迭代规则。
查漏补缺
讲到这里,忽然记起在上一篇文章中我们并未对 SDE class 实现数值离散方法 discretize()..

当时只在子类 VPSDE 和 VESDE 中实现了,因为后两者的离散形式分别就是 SMLD 和 DDPM,所以当时就直接把相应的代码实现(指它俩的 discretize() 方法)也撸掉了。既然如此,现在我们就赶紧为父类 SDE 补上 discretize() 方法,包括正向和逆向两个方向的 SDE 数值离散形式。
先来回顾下,在上一篇文章中SDE class 里已实现的部分:
import abc
import torch
from typing import Callable, Union, Tuple
from torch import Tensor
from torch.nn import Module
class SDE(abc.ABC):
def __init__(self):
super().__init__()
@property
@abc.abstractmethod
def T(self) -> int:
""" 正向 SDE 的终止时刻, 整个过程时间的流动方向是 0 -> T """
pass
@abc.abstractmethod
def sde(self, x: Tensor, t: Tensor) -> Tuple[Tensor, Tensor]:
""" 计算漂移和扩散系数: f, g """
pass
@abc.abstractmethod
def p_0t(self, x: Tensor, t: Tensor):
""" 计算决定条件分布 p(x(t) | x(0)) 的参数,这里计划会返回均值和标准差 """
pass
def prior_sampling(self, shape):
""" 从先验分布 p_T(x) 中采样,先验通常为标准高斯分布 """
return torch.randn(*shape)
def reverse(self, score_fn: Union[Module, Callable]):
""" 构造逆向时间的 SDE, 返回1个代表 reverse-time SDE 的对象 """
T = self.T
# 用于计算正向 SDE 的漂移和扩散系数的函数
fw_sde = self.sde
class RSDE(self.__class__):
@property
def T(self) -> int:
return T
def sde(self, x: Tensor, t: Tensor) -> Tuple[Tensor, Tensor]:
# 正向 SDE 的漂移和扩散系数
f, g = fw_sde(x, t)
score = score_fn(x, t)
# 根据 reverse-time SDE 公式重新计算漂移系数
f = f - g[:, None, None, None] ** 2 * score
return f, g
return RSDE()
如今补上 discretize() 方法,同时在 RSDE class 中也对应做修改,至于具体的数值方法,我们就选用 Euler-Maruyama 吧,毕竟名气大,连我这种孤陋寡闻的都知道它。
class SDE(abc.ABC):
def __init__(self, N: int):
super().__init__()
# 补上离散形式所需的总时间步: number of timesteps
self.N = N
# ... 省略之前已实现的部分 ... #
def discretize(self, x: Tensor, t: Tensor) -> Tuple[Tensor, Tensor]:
""" 使用数值方法对 SDE 实施离散化, 返回 $f * \Delta t$, $g * \sqrt{\Delta}t$ """
# 欧拉-丸山法所对应的离散时间间隔
delta_t = 1. / self.N
f, g = self.sde(x, t)
return f * delta_t, g * torch.tensor(delta_t).to(t).sqrt()
def reverse(self, score_fn: Union[Module, Callable]):
""" 构造逆向时间的 SDE/ODE, 返回1个代表 reverse-time SDE 的对象 """
N = self.N
T = self.T
# 用于计算正向 SDE 的漂移和扩散系数的函数
fw_sde = self.sde
fw_discretize = self.discretize
class RSDE(self.__class__):
def __init__(self):
self.N = N
@property
def T(self) -> int:
return T
def sde(self, x: Tensor, t: Tensor, discrete: bool = False) -> Tuple[Tensor, Tensor]:
# 正向 SDE 的漂移和扩散系数
f, g = fw_discretize(x, t) if discrete else fw_sde(x, t)
score = score_fn(x, t)
# 根据 reverse-time SDE 公式重新计算漂移系数
f = f - g[:, None, None, None] ** 2 * score
return f, g
return RSDE()
在原 SDE 中, sde() 方法返回的是漂移系数和扩散系数,即:
;而在离散形式的 discrete() 方法中,返回的则分别是漂移系数与时间间隔的乘积以及扩散系数与时间间隔的开根的乘积,即:
。
对于 reverse-time SDE 的离散形式则可以很方便的在原有 sde() 方法上进行修改,只要将原本调用 sde() 方法改为调用 discrete() 方法即可,其余的计算逻辑无需改变,最终返回的恰好是 ,与公式一致。
Em.. 怎么隐约嗅到了 bug 的味道,心里感觉有只鬼不断在我耳边叫:

OH! 在上一篇文章中实现的子类:VESDE, VPSDE 和 subVPSDE 在调用父类 SDE 的 初始化方法时没有传入参数 N,这是因为如今 SDE class 的 __init__() 方法中规定了参数 N 需要显式传入,也就是说,需要将三个子类的 super().__init__() 改为 super().__init__(N) :
class VESDE(SDE):
def __init__(self, sigma_min: float = 0.01,sigma_max: float = 50., N: int = 1000):
super().__init__(N)
# ... 省略之前已实现的部分
# ...
class VPSDE(SDE):
def __init__(self, beta_min: float = 0.1, beta_max: float = 20., N: int = 1000):
super().__init__(N)
# ... 省略之前已实现的部分
# ...
class subVPSDE(SDE):
def __init__(self, beta_min: float = 0.1, beta_max: float = 20, N: int = 1000):
super().__init__(N)
# ... 省略之前已实现的部分
# ...
同时,原来在子类中的 self.N = N 可以省去,因为在父类 SDE 中已经有了这句。
ps: 感谢@目光(www.zhihu.com/people/497178101903d6c76916541222aa2d58)特意私信指正以上三个子类的“疏忽”,这是 CW 文章与 notebook 中的 code 没有同步好而导致的,要是知乎能够有 github 对于代码的 sync up 功能该多好~

至于 reverse diffusion sampler 的代码实现,我们先 hold 住,酝酿一下,待下一节内容阐述完毕后再来撸~

原创:PC Sampling
在上一篇文章的开头,CW 讲过由于 reverse-time SDE 依赖于 score,这使得我们可以在原有采样过程中同时使用 score-based MCMC 这类采样方法,因为它们也依赖于 score,既然大家需求一致,何不一起玩呢,是吧~

秉持着两个臭皮匠胜过一个周瑜(周瑜:你点错人了叭..)的信念,

作者自创了一招——交替使用 reverse-time SDE(当然,要对其使用数值方法进行离散) 和 score-based MCMC 采样方法,并且将 reverse-time SDE 视作 "predictor" 角色;同时将 score-based MCMC 视作 "corrector" 角色,也就是说将后者视为对前者的校正,这招也被命名为 "PC sampling"。
作者发明这招当然是希望最终采样结果能够比仅使用一种采样方式(即仅用 reverse-time SDE or score-based MCMC 其中之一)来得强,目前看来这更多是一种信念驱使。然而,对于这种信念,作者是有实验支撑的,同时使用两种采样方法在大多数场景确实比单独使用一种能打(详情请各位客官参考 paper)。
score-based MCMC 采样方法有很多种,为了延续作者自己以往的工作(不用猜,点名 NCSN(https//arxiv.org/abs/1907.05600),于是就拍脑袋地选择了 (annealed)Langevin dynamics。

其中 step size 取决于信噪比(signal-to-noise ratio) 、高斯噪声的第 2 范数 以及 score 的第2范数 。并且,当 batch size 较大时,会对这几个范数在整个 mini-batch 中做平均;而当 batch size 较小时,作者则建议将 替换为 ,其中 是 的维度。
神马? 不知道啥是 Langevin dynamics?

好吧.. 还请您参考 CW 往年的吹水文:
图像生成别只知道扩散模型(Diffusion Models),还有基于梯度去噪的分数模型:NCSN(Noise Conditional Score Networks)
https://zhuanlan.zhihu.com/p/597490389
将 PC sampling 分别应用于 VE SDE 和 VP SDE,可表示为如下过程:

Tips: 通常在实现时,会令 corrector 在前、predictor 在后,并且两者都仅有一步(one step) ,而非像上图所示每步 predictor 之后有多步 corrector。
让世界更清晰:Tweedie's formula
另外,作者在论文中还提到,不论是 DDPM 还是 SMLD,它们生成的样本通常都包含一些肉眼难以观察的噪声(忍不住吐槽:既然难以看出,那你又知道?),进而导致 FID 很难看,如以往的这篇 paper(https//arxiv.org/abs/2009.05475) 所述(哦,原来是有大佬验证过的,好叭~)。

并且,正是这个原因,导致 SMLD 通常在 FID 评测上干不过 DDPM,因为后者在采样的最后一步有进行去噪,而前者则没有。在知道了这个真相后,作者就在采样的最后一步使用去噪。靠谱的人做事都得有所依据,而作者去噪的“依据”就是 Tweedie's formula(https//stacks.stanford.edu/file/druid%3Avc631wx1024/BIO%2520256.pdf)。

讲人话就是在采样到最后一步时,不加上高斯噪声那一项(比如在以上 predictor 部分的最后不加上含有 的那一项)。算了,还是稍微讲一下 Tweedie's formula 为何等价于去掉高斯噪声 那一项吧,不讲总感觉不舒服,谁让我 CW 天生就爱吹水呢~

Tweedie's formula 计算的是随机变量 的均值 的后验期望:
,其中 是随机变量的方差,而 就是我们熟悉的 score 了。巧妙的是,在 NCSN 中, score 与 高斯噪声的关系是 : (不知道为何的小可爱们去复习 在前面贴出来的那篇文章),代入到 Tweedie's formula 便得到: 。
注意,此处的 正是上图 Algorithm2 中 Predictor 部分最后的 ,因为 。于是,根据 Tweedie's formula 在最后一步采样时进行去噪就是将 减去 ,这其实就等于 ,相当于在最后一步采样时计算出 后就不需要再加上 了。

劳动时刻:Coding Time
现在,我们可以将 pc sampling 连同前面的 reverse diffusion sampling 一并实现。由于 predictor 和 corrector 都并非指某种具体的方法,而是指代一类方法,因此这两者可以被实现为抽象基类(abstract class),然后具体的采样方法就可以被实现为继承 predictor 或 corrector 的子类,比如 reverse diffusion sampling 就应当作为 predictor 的子类。
先来把 predictor 和 corrector 所对应的抽象基类给实现了,同时将 pc sampling 的整个采样流程也撸掉。在每个采样时间步,先使用 corrector 再使用 predictor,并且 corrector 预测一次后就紧接着使用 predictor 预测,不断交替使用两者。
class Predictor(abc.ABC):
def __init__(self, sde: SDE, score_fn: Union[Module, Callable]):
super().__init__()
self.sde = sde
self.rsde = sde.reverse(score_fn)
self.score_fn = score_fn
@abc.abstractmethod
def update_fn(self, x: Tensor, t: Tensor) -> Tuple[Tensor, Tensor]:
pass
class Corrector(abc.ABC):
def __init__(self, sde: SDE, score_fn: Union[Module, Callable], snr: float, n_steps: int):
super().__init__()
self.sde = sde
self.score_fn = score_fn
self.snr = snr
self.n_steps = n_stpes
@abc.abstractmethod
def update_fn(self, x: Tensor, t: Tensor) -> Tuple[Tensor, Tensor]:
pass
@torch.no_grad()
def pc_sampling(
sde: SDE, sample_shape,
predictor_fn: Callable, corrector_fn: Callable,
eps: float = 1e-3, denoise: bool = True,
device: Union[str, int] = "cuda"
) -> Tensor:
x = sde.prior_sampling(shape).to(device)
timesteps = torch.linspace(sde.T, eps, sde.N, device=device)
for t in timesteps:
t = t.repeat(x.size(0))
x, x_mean = corrector_fn(x, t)
x, x_mean = predictor_fn(x, t)
return x_mean if denoise else x
最后在返回采样结果前,若 denoise = True ,则使用 Tweedie's formula 去噪,也就是返回采样的均值 x_mean;否则,直接返回采样最后一步的结果 x 。
晾了很久的 reverse diffusion sampling 现在终于有机会被实现了!

实现它的关键逻辑就是调用 RSDE class 的 sde() 方法并指定参数 discrete = True,这样就能得到 ,然后根据 (i) 式的迭代规则就可以计算出采样结果。
class ReverseDiffusionPredictor(Predictor):
def __init__(self, sde: SDE, score_fn: Union[Module, Callable]):
super().__init__(sde, score_fn)
def update_fn(self, x: Tensor, t: Tensor) -> Tuple[Tensor, Tensor]:
f_delta_t, g_sqrt_delta_t = self.rsde.sde(x, t, discrete=True)
x_mean = x - f_delta_t
x = x_mean + g_sqrt_delta_t[:, None, None, None] * torch.randn_like(x)
return x, x_mean
class EulerMaruyamaPredictor(Predictor):
def __init__(self, sde: SDE, score_fn: Union[Module, Callable]):
super().__init__(sde, score_fn)
def update_fn(self, x: Tensor, t: Tensor) -> Tuple[Tensor, Tensor]:
dt = -1. / self.rsde.N
f, g = self.rsde.sde(x, t)
x_mean = x + f * dt
x = x_mean + g[:, None, None, None] * np.sqrt(-dt) * z
return x, x_mean
考虑到欧拉-丸山(Euler-Maruyama)法是在众多数值方法中比较出圈,于是以上就顺带将其也一并实现了。
接下来就轮到 Langevin dynamics 这个属于 score-based MCMC 类型的采样方法了,它因为是作为 corrector 的存在,所以要被实现为 Corrector 的子类。要注意 step size
的设置,作者给出的计算规则如下:

其余也没有太多可说的了,开干吧~!

class LangevinDynamicsCorrector(Corrector):
def __init__(self, sde: SDE, score_fn: Union[Module, Callable], snr: float, n_steps: int):
super().__init__(sde, score_fn, snr, n_steps)
def update_fn(self, x: Tensor, t: Tensor) -> Tuple[Tensor, Tensor]:
if isinstance(self.sde, VPSDE):
timestep = (t / self.sde.T * (self.sde.N - 1)).long()
alpha = self.sde.alphas[timestep].to(t.device)
else:
alpha = torch.ones_like(t)
def get_norm(ts: Tensor) -> Tensor:
return torch.norm(ts.reshape(ts.size(0), -1), dim=-1).mean()
for _ in range(self.n_steps):
score = self.score_fn(x, t)
z = torch.randn_like(x)
# (B,)
score_norm = get_norm(score)
# (B,)
z_norm = get_norm(z)
# (B,)
step_size = 2 * alpha * (self.snr * z_norm / score_norm) ** 2
x_mean = x + step_size[:, None, None, None] * score
x = x_mean + torch.sqrt(2 * step_size)[:, None, None, None] * z
return x, x_mean
class NoneCorrector(Corrector):
def __init__(self, sde: SDE, score_fn: Union[Module, Callable], snr: float, n_steps: int):
pass
def update_fn(self, x: Tensor, t: Tensor) -> Tuple[Tensor, Tensor]:
return x, x
考虑到 corrector 更多是作为打辅助的存在,因此它并不是必需品,那么将其在 pc sampling 踢掉后,整个采样流程就成为 "predictor-only" 了。于是,为了适配这种情况,我们可以实现一个“假的 corrector”即以上 NoneCorrector 这个类, 它啥事都不干(妥妥的躺平一族)——直接将输进来的变量返回。同理,也可以考虑设置一个 NonePredictor class,这样整个采样流程就成为 "corrector-only"(至于具体的实现就交给各位友友们啦,CW 先行告辞~)。

高效 Boy:Probability Flow Sampling
形如 的伊藤 SDE 有对应的如下 ODE 形式:

作者在附录 D 中给出了证明,CW 在以下这篇回答中也间接给出了证明过程:
扩散模型中的Reverse Time SDE是怎么推导得到的呢?(https://www.zhihu.com/question/629085800/answer/3421808487)
这个 ODE 形式被作者取名为 "probability flow ODE"。不难发现,它的样子和 reverse-time SDE 长得还蛮像的,最主要的区别是它没有随机项(i.e. 布朗运动 )。它最主要的功能是采样,由于不含随机的布朗运动项,因此整个采样过程是一条确定性的轨迹,也就是只要知道了采样起点,就可以根据以上公式唯一确定最终的采样结果,作者将这个采样方法命名为 "probability flow sampling"。
与 reverse-time SDE 一样,任何通用的数值求解器都可作用于 probability flow ODE,从而形成不同的采样方式。按单位时间步 将其离散化,就会得到以下迭代规则:

若对 VE SDE 和 VP SDE 应用这个迭代规则,就会分别得到:


再次发现,以上两个式子和前面 reverse diffusion sampling 中的也挺像。这也是符合预期的,毕竟 probability flow ODE 和 reverse-time SDE 就长得很像。所以,对于以上两个式子你们不用费劲地重新推导,只需在 reverse diffusion sampling 公式的基础上,去掉随机项(含有 那项)并对应改下系数即可。当然,你要重新推导 CW 也不拦你,思路和前面我们推导 reverse diffusion sampling 几乎是一样的。
由于业界大佬们已经开发出许多高效计算的黑盒 ODE 求解器,因此我们可以借助这些黑盒求解器来解 probability flow ODE,这也导致使用 probability flow sampling 通常比 reverse diffusion sampling 来得快,可谓是高(搞)效(笑) boy 一枚~

但是,使用前者所生成的样本的 FID 却通常比后者来得烂。另外,作者提到,probability flow ODE 的采样质量取决于其对应的 SDE 形式。比如在面对高维数据时,同样是使用 probability flow sampling,VE SDE 所生成的样本质量就不如 VP SDE。

动手擼代码啦
在实现 probability flow sampling 前,我们有一些小工作需要提前完成。因为前面实现的 SDE class 并不具备 ODE 的逻辑,而聪明的你们一定体会到 ODE 可作为 SDE 的特例来看待,所以只需要对 SDE class 稍微改造下(不需要整容)即可适配需求。准确来说,是对其中的 RSDE class 进行修改,因为 probability flow ODE 主要用于采样,而采样是个逆向过程,所以与 reverse-time SDE 相对应。
改造的方法很简单,只需在 SDE class 的 reverse() 方法中加多一个布尔类型的参数来指代是否要使用 probability flow sampling 进行采样(以便和 reverse diffusion sampling 区分),干脆就将该参数命名为 probability_flow。然后,在 RSDE class 中的 sde() 方法里加多一个判断,若 probability_flow = True,那么就将扩散系数置 0,即:g= g * 0.。
def reverse(self, score_fn: Union[Module, Callable], probability_flow: bool = False):
""" 构造逆向时间的 SDE/ODE, 返回1个代表 reverse-time SDE 的对象 """
N = self.N
T = self.T
# 用于计算正向 SDE 的漂移和扩散系数的函数
fw_sde = self.sde
fw_discretize = self.discretize
class RSDE(self,__class__):
def __init__(self):
self.N = N
self.probability_flow = probability_flow
@property
def T(self) -> int:
return T
def sde(self, x: Tensor, t: Tensor, discrete: bool = False) -> Tuple[Tensor, Tensor]:
# 正向 SDE 的漂移和扩散系数
f, g = fw_discretize(x, t) if discrete else fw_sde(x, t)
score = score_fn(x, t)
# 根据正向 SDE 的漂移和扩散系数计算逆向时间 SDE 的漂移和扩散系数
f = f - g[:, None, None, None] ** 2 * score * (0.5 if self.probability_flow else 1.)
# 如果是 ODE, 则没有扩散系数, 设为 0
if self.probability_flow:
g = g * 0.
return f, g
return RSDE()
Ready to Go~! 现在可以真正来实现 probability flow sampling 了。

利用黑盒求解器求解 probability flow ODE 可以使用 scipy 的接口:scipy.integrate.solve_ivp(https//docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.solve_ivp.html),这个接口常被用于求解 ODE 的初值问题(initial value),而我们这里的初值就是作为采样起点的先验。不过,也可以考虑使用某些指定的 latent code 作为采样起点,以达到控制采样行为的目的。
另外,由于 probability flow ODE 不含随机项,因此无法直接使用 Tweedie's formula 去噪。于是,可以考虑在采样的最后一步加入包含随机项的那些采样方法,比如 reverse diffusion sampling,使用它来额外做多一步采样,然后将其返回的采样均值作为去噪后的结果。
from scipy import integrate
def ts_to_flattened_np(ts: Tensor) -> np.ndarray:
return ts.detach().cpu().numpy().reshape((-1,))
def flattened_np_to_ts(arr: np.ndarray, shape) -> Tensor:
return torch.from_numpy(arr.reshape(shape))
@torch.no_grad()
def probability_flow_sampling(
sde: SDE, sample_shape, score_fn: Union[Module, Callable],
latent: Tensor = None, denoise: bool = False,
method: str = "RK45", rtol: float = 1e-5, atol: float = 1e-5,
eps: float = 1e-3, device: Union[int, str] = "cuda"
) -> Tuple[Tensor, int]:
# 可以根据指定的 latent code 作为采样起点
x = sde.prior_sampling(sample_shape).to(device) \
if latent is None else latent
dtype = x.dtype
def get_ode_drift(x: Tensor, t: Tensor) -> Tensor:
""" 计算 probability flow ODE 的漂移系数. """
# probability flow ODE 作为 reverse-time SDE 的特例
# 由参数 probability_flow = True 指定
rsde = sde.reverse(score_fn, probability_flow=True)
# 取索引0代表漂移系数; 索引1对应的是扩散系数(这里是0)
drift = rsde.sde(x, t)[0]
return drift
def ode_fn(t: float, x: np.ndarray) -> np.ndarray:
x = flattened_np_to_ts(x, sample_shape).to(device=device, dtype=dtype)
t = torch.ones(x.size(0), device=device) * t
f = get_ode_drift(x, t)
return ts_to_flattened_np(f)
solution = integrate.solve_ivp(
ode_fn, (sde.T, eps), ts_to_flattened_np(x),
rtol=rtol, atol=atol, method=method
)
# 取索引 -1 对应终止时刻的状态
x = flattened_np_to_ts(solution.y[:, -1]).to(device=device, dtype=dtype)
def denoise_fn(x):
""" 由于 probability flow ODE 不含随机项, 因此无法直接使用 Tweedie's formula 去噪,
这里使用 reverse diffusion sampling 在最后时刻进行采样作为去噪步骤 """
t = torch.ones(x.shape[0], device=device) * eps
predict_fn = ReverseDiffusionPredictor(sde, score_fn).update_fn
# 使用 reverse diffusion predictor 在最后时刻的采样均值作为去噪结果,
# 取索引1代表采样均值
x_mean = predict_fn(x, t)[1]
return x_mean
if denoise:
x = denoise_fn(x)
# 数值求解 ODE 所经历的迭代次数(离散时间步数)
nfe = solution.nfev
return x, nfe
外族乱入:Ancestral Sampling for SMLD
宋飏大佬之前在设计 SMLD 时,采样方法用的是 Langevin dynamics(毕竟人家连名字都含有"LD"字样)。后来看到 DDPM 站上舞台后,发现其实 SMLD 也可以玩同样的套路——祖先采样(https//www.reddit.com/r/deeplearning/comments/cgqpde/what_is_ancestral_sampling/)(DDPM 的采样方式就是祖先采样)。

SMLD 想要玩祖先采样,当务之急是先根据 推导出条件分布 ,从而建立起马尔科夫链: ; 这一步解决之后,就按照 DDPM 的套路使用贝叶斯定理推导出逆向的 ;最终,SMLD 就可以顺利得到如下所示的祖先采样:

具体推导过程在论文的附录 F 部分,思路和 DDPM 的一样,CW 就不在这里啰嗦了(因为是无聊的风格),我很有信心大家都是先有了 DDPM 基础才逛到这里的~

大方给出代码实现
虽然祖先采样不是本论文原创,算是“外族”,但我们大方人也就顺带大方地给出相应的代码实现吧~

浅浅地思考了一下,祖先采样可被为 Predictor 子类,而代码实现的核心就是以上公式,没有太多可言。
class VEAncestralSamplingPredictor(Predictor):
def __init__(self, sde: SDE, score_fn: Union[Module, Callable]):
super().__init__(sde, score_fn)
if not isinstance(sde, VESDE):
raise ValueError(f"sde must be an object of VESDE class, but current is: {type(sde)}")
def update_fn(self, x: Tensor, t: Tensor) -> Tuple[Tensor, Tensor]:
T, N = self.sde.T, self.sde.N
timestep = (t / T * (N - 1)).long()
# \sigma_i
sigma = self.sde.discrete_sigmas.to(t.device)[timestep]
# \sigma_{i-1}
# 当 \sigma_i 为 \sigma_{min} 时,
# \sigma_{i-1} 就是 \sigma_0 = 0
adj_sigma = torch.where(
timestep == 0,
torch.zeros_like(t),
self.sde.discrete_sigmas.to(t.device)[timestep - 1]
)
# 以下根据论文公式(47)进行计算
delta_sigma_square = sigma ** 2 - adj_sigma ** 2
score = score_fn(x, t)
x_mean = x + delta_sigma_square * socre
std = (adj_sigma ** 2 * delta_sigma_square / sigma ** 2).sqrt()
x = x_mean + std * torch.randn_like(x)
return x, x_mean
需要稍微注意的是
即以上代码中 adj_sigma 的计算。当 timestep =0 即
(以上代码中的 sigma ) 为
时,
就要设为
,即 adj_sigma =0 ,因为 discrete_sigmas [0] 对应的是
。
Stay Tuned
虽然经过两篇文章后,模型的训练和采样过程都解析完毕,但本系列还没完,毕竟这篇 paper 可圈可点的内容确实不少。生成模型最好的玩应该是各种条件生成,比如:文生图、图像修复、图像上色 等。所以,CW 会下篇文章的主题将会是条件生成,届时将携手各位友友们一起来深入了解下在 score-based SDE 的玩法下是如何应对条件生成场景的,See u~


公众号后台回复“数据集”获取100+深度学习各方向资源整理
极市干货

点击阅读原文进入CV社区
收获更多技术干货


