导语：非线性规划是一种应用场景甚广的优化问题，从神经网络训练的反向传播，到资产组合的配置优化，都离不开寻找非线性函数的极小点的技巧。本文将讲解无约束非线性规划的基本思路和一些简单的算法。
阅读本文需要掌握线性代数和多元微积分的知识。
建议读者对数学规划有基本了解。
无约束非线性规划问题
无约束的非线性规划问题具有以下形式
这里 f:R^n→R 是一个连续函数。但只是单纯的连续函数是很难被优化的，我们一般会要求函数 f 满足 C^1 或者 C^2 的性质，这些性质在之后会有定义。
这种问题叫做“无约束”因为它的可取点是任何 x∈R^n；相对应的，有约束的规划问题一般有以下形式
这里 g1,…,gm 是一些约束函数，而 b1,…,bm 是一些实数。
在解决非线性规划问题时，我们最想做的是计算出一个全局极小点。什么是全局极小点呢？
定义. 一个函数 f 的全局极小点（global minimizer） 是一个 x∗∈R^n，其满足对于任何一个 x∈R^n 都有 f(x∗)≤f(x)。
但是找出函数的全局极小点只是我们的理想，这其实是非常困难的，而找出一个局部极小点是我们能做的最好的尝试。
定义. 一个函数 f 的局部极小点（local minimizer）是一个 x∗∈R^n，其满足，存在 R^n 中的一个开集 N∋x∗，对于所有 x∈N 有 f(x∗)≤f(x)。这个定义有时也称作弱局部极小点（weak local optimizer），因为它允许在局部内有和它取值相同的点。
定义. 一个函数 f 的强局部极小点（strong local optimizer）是一个 x∗∈R^n，其满足，存在 Rn 中的一个开集 N∋x∗，对于所有 x∈N 并且 x≠x∗ 有 f(x∗)<f(x)。
不过我还有一个坏消息，其实局部极小点我们可能也找不到。嗯，不行。但是我们可以做到的，是找到一个足够接近局部极小点的向量，以至于 f 在该位置的取值非常接近实际的局部最小值。这就是本文中介绍的算法要达成的目标。
定义和符号
在一切开始之前，我们有必要讲清楚文中用到的数学符号和它们的定义。首先是关于微分的三个定义：
定义. 设 f:R^n→R 是一个连续函数，用 {x1,…,xn} 表示 R^n 的标准基。如果对于所有满足 l1+…,+ln=m 的 l1,…,ln≥0，m 阶导数
存在并且是连续的，我们说 f 是一个 C^m 函数。
定义. 设 f:R^n→R 是一个 C^1 函数，那么 f 的\emph{梯度(gradiet)}是一个连续函数 ∇f:R^n→R^n，定义为
高维函数的梯度和在一维函数的导数是同等的概念，它告诉我们一个函数在某点向各个方向的斜率是多少，通过这个信息我们可以寻找坡度向下的方向进行优化。
定义. 设 f:R^n→R 是一个 C2 函数，那么f 的海塞矩阵（Hessian matrix）是一个连续函数 ∇2f:R^n→R^(n×n)（有时也写作 Hf），定义为
然后是线性代数中（半）正定矩阵的定义：
定义. 对于一个 n×n 矩阵 A∈R^(n×n)，如果 A=AT 并且对于每一个向量 x∈Rn 有xTAx≥0，我们说 A 是一个半正定矩阵（positive semi-definite matrix）。
定义. 对于一个 n×n 矩阵 A∈R^(n×n)，如果 A=AT 并且对于每一个向量 x∈Rn∖{0} 有 xTAx>0，我们说 A 是一个正定矩阵（positive definite matrix）。
下面是两个至关重要的定理，读者也可以在微积分的教材里找到它们。
两个定理
首先是一个在多元微积分中很常见的定理，它告诉我们如何判别一个函数的（强）局部极小点。
定理 1. 设 f:R^n→R 是一个 C^2 函数，并且设 x∗∈R^n。如果 ∇f(x∗)=0 并且 ∇2f(x∗) 是一个半正定矩阵，那么 x∗ 是 f 的一个局部极小点；如果 ∇f(x∗)=0 并且 ∇2f(x∗) 是一个正定矩阵，那么 x∗ 是 f 的一个强局部极小点。
你也许想到，啊哈！我们用这个定理的结论不就可以解决最小化问题了吗？为什么说不能找到极小点？
那是因为，找到一个函数（在这里就是梯度 ∇f）的零集其实也是千古难题，有时我们甚至会用非线性优化问题来估测一个函数等于零的位置。所以呐，还是老老实实地继续往下看吧。
下面的泰勒定理可以帮助我们分析函数在一个局部里的表现，方便我们找到极小点。
定理 2.（泰勒定理） 设 f:R^n→R 是一个 C^1 函数，并设 p∈R^n。那么存在某个 t∈(0,1)，有
并且，如果 f 是 C^2 函数，那么存在某个 t∈(0,1)，有
这个定理告诉我们，选定 R^n 上的一个点 x 和一个方向 p，函数 f 从 x 到 x+p 的变化等于 f 在某一点的梯度和向量 p 的点积，而这个点总能在 x 和 x+p 之间找到。
依照这个定理，我们还可以在仅知 f(x) 和 ∇f(x) 的情况下在局部内线性估测 f 的值。我们已知对于任何 p∈R^n，有
可是每一个 p 对应着不同的 t，用这个方法来计算 f(x+p) 并不方便。但是，如果我们允许一定误差的话，可以用 ∇f(x) 代替 ∇f(x+tp) 来进行估测，有
因为
所以如果 p 足够小，那么（由于 ∇f 是连续的）∇f(x)−∇f(x+tp) 的差也很小，以至于等式右侧的误差同样很小。
从基础微积分的知识中，我们知道如果 f 是一个一维函数，那么上面的做法是以 (x,f(x)) 为中心画出了一条切线（也就是一阶泰勒展开）
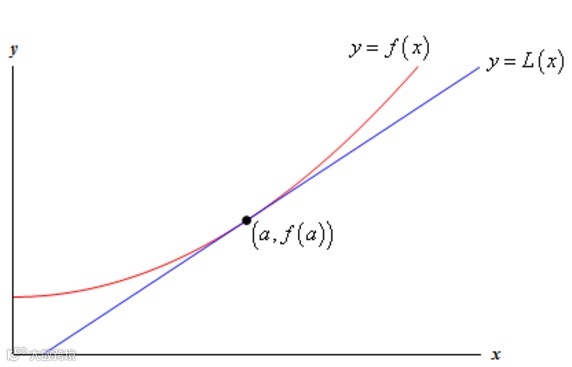
这条切线在一定范围之内和实际函数非常接近。在更高维度中，函数 ϕ(p)=f(x)+∇f(x)^Tp 的图像则构成以 (x,f(x)) 为中心的一个超切面。
泰勒定理中的第二个公式同样给了我们估测方法
这个用到了二阶项的估值会比之前的估测更准确；使用这个估值的要求更高一点，需要 f 是 C^2 函数（在实际应用中基本都可以满足）。
泰勒定理为我们提供了一种搜索一个函数极小点的方法。假设 x 不是函数 f 的局部极小点并且我们知道 f 在一个点 x 的取值 f(x) 以及梯度 ∇f(x)，如果选得一个方向 p∈R 满足 ∇f(x)Tp<0，那么存在某个 α>0，使得 f(x+αp)<f(x)。如此重复，在第 k 次迭代是从 xk 开始，找到合适的 pk 和 αk 并更新 xk+1=xk+αkpk，这样，让 f(xk) 的取值越来越小，以收敛到一个局部极小点。
以上的方法叫做线搜索（line search），是解决非线性规划问题的一类主要方法。线搜索的主要问题在于要寻找合适的方向（direction）pk 和步长（step length）αk。
方向
在线搜索的每一次迭代中，我们想要方向 pk 满足 ∇f(xk)Tpk<0。我们知道向量 ∇f(xk) 和 pk 之间的角度 θk 满足
因此符合条件的 pk 也恰恰是和梯度 ∇f(xk) 的角度大于 90∘ 的向量。下面介绍选取方向 pk 的几个常用的方法。
梯度下降
最符合直觉的方向是选择 f 下降幅度最大的方向。也就是说，固定 p 的长度不变，我们想找到最小的 ∇f(xk)Tp。于是乎，我们解决一个简单的最小化问题
用 θ 表示 p 和 ∇f(xk) 之间的角度，有
很明显，当 cosθ=−1 时这个值被最小化，对应向量 p⋆=−∇f(xk)/||∇f(xk)||。因此，作为最大下降的方向，可以选择 pk=−∇f(xk)，这个方向一般称为梯度下降（gradient descent）或者最大下降（steepest descent）。
最大下降方法的优点有两个。一是它保证全局的收敛性：不论我们的起始点 x0 在哪里，反复的迭代都会收敛向一个局部极小点。第二是它对函数 f 的要求很小，只需要 f 是连续可导的。但同时，它的缺点也很明显，那就是它在很多情况下的收敛速度很慢。最大下降的方向与 f 在 xk 的水平集 {x∈Rn:f(x)=f(xk)} 程垂直关系，因此根据起始点的位置，很可能在迭代中画出锯齿形的低效率路径。
上图是一个二次函数 Q(x)=3x1^2+2x1x2+3x2^2 的热力图，它的最小值在 (0,0) 的位置。图中的三根曲线是从三个不同的点起始的梯度下降方法的搜寻路径，线段每变换一次代表一次迭代，其中每一条曲线都在 11 到 14 次迭代中找到了距离极小点误差小于 0.00001 的位置。当然了，二次函数一般都比较规整，梯度下降算法的表现还算不错，下面的例子就不太好了。
上图中的是 Rosenbrock 函数 R(x)=(1−x1)^2+100(x2−x1^2)^2，它的极小点在 (1,1)（图中红点）。可以在热力图上看出这个函数的表现不是那么友好，它挖了一个又弯又窄的沟，函数的梯度指向的不是沟的下游而是沟的中央，所以梯度下降法像在编小辫一样地反复地折返，用了 5491 次迭代才从 (−0.5,1)（图中绿点）达到与极小点的误差小于 0.00001 的位置。
我们放大算法在沟里搜索的路径，足以看出它多没有效率。
那碰上这种奇葩的函数我们该怎么办呢怎么办呢？往下看。
牛顿方法
另一个重要的衰减方向（可能可以说是最重要的）是牛顿方向（Newton's direction）。记得在泰勒定理中，二次可导的函数 f 在 xk 附近的二次泰勒估值是
（这里 =:mk(p) 是指我们把 mk(p) 定义为等号左边的表达式）。暂时假设 ∇2f(xk) 是一个正定矩阵，我们想将二次估值 mk(p) 最小化，那么求一阶导数得到
将它设为 0，求得
因为 mk 的二次导数是 ∇2f(xk)，在假设中是正定矩阵，根据定理 1.，上面所求 pk 确定是极小点。
理论上来说，牛顿方法的收敛速度要比梯度下降更快，因为梯度下降使用的是一次展开进行来估测方向，误差一般在 O(∥pk∥2)；而牛顿方法使用二阶展开，误差一般在O(∥pk∥3)，所以选择的方向会更准确。可以理解为，牛顿方法选择的方法更有“远见”，因为梯度下降的方向虽然在眼前的下降速度是最快的，但是在跑出一定距离之后就会比牛顿方向的表现差，所以要重新选择方向的次数比牛顿方法更多。
当然，牛顿方法的缺点也比较明显：首先它需要函数 f 是二次可导的，并且需要在 xk 的海塞矩阵 ∇2f(xk) 是正定的（这一般需要起始点 x0 距离极小点足够近）。再者，即使 ∇2f(xk) 是正定的，方向 pk 也不一定是降低方向，有可能 f(xk+pk)>f(xk)。而且计算 f 的海塞矩阵再求它的逆矩阵有时也需要很大的计算量。牛顿方法的种种缺陷都有相应的解决方法，本文中不进行探索，可以期待未来的文章中的讲解。
一个比较直接地使用牛顿方向的算法就是在 ∇2f(xk) 为正定的时候使用牛顿方向，而不是的时候使用梯度下降，这样可以在足够接近局部极小点的时候以高效率收敛。判断正定矩阵的方法也并不困难，因为一个对称矩阵是正定的当且仅当它的所有特征值(eigenvalues)都是大于零的，这个用矩阵计算库（比如 Numpy）都可以计算出来。
我们来看牛顿方法在二次函数 Q(x) 上的计算。
居然一次就找到了最优解！但是稍微仔细想一下，二次函数的二次泰勒展开并不只是在局部估测这个函数，而是完全就等于这个函数。所以当我们最小化了二次泰勒展开时，实际上已经找到问题的极小点。好，我们看一下创造困难的 Rosenbrock 函数。
牛顿方法用了 31 步就找到了误差小于 0.00001 的近似解，相比于梯度下降的 5491 步是一个巨大的进步。不得不说，函数的二次导数 ∇2R 中包含了这条壕沟的很多秘密。梯度下降和牛顿方法的表现差异在放大的图里一目了然。
步长
上面介绍了每一步从 xk 出发的方向 pk，但这还不够，我们还需要选择一个在这个方向上行走的步长 αk 以达到新的点 xk+αkpk。在选择每一次迭代的步长时，我们都面临一个权衡：如果一步过长了，那么可能会走得太远，跨过了极小点；如果一步太短，那么并不能将目标函数 f 的取值降低太多。
最大下降步长
一个最直接最“贪心”的步长选择是在射线 {xk+αpk:α≥0} 上 f 取值最小的点。也就是说，解决一个最小化问题
并以求出的极小点作为步长 α。这是一个在一维切片上的优化问题，将导数设为 0，
（运算中使用了高维版的链式法 (f∘g)′(x)=∇f(g(x))Tg′(x)）可以看出极值出现在 f 的梯度和方向 pk 垂直的位置。不巧的是，等式右侧函数的零点可能并不好求，一般来说寻找一个“足够好”的步长会比计算上面的“最好”步长更有效率。那我们怎么判断一个步长是不是足够好呢？接下来的 Wolfe 条件是一个常用的辨别方法。
Wolfe 条件
在 Wolfe 条件中有两个不等式，需要首先选取 c1∈(0,1) 以及 c2∈(c1,1) 作为参数。条件中的第一个不等式要求步长 α 满足
也就是说，从 xk 到 xk+αpk 的移动对 f 的缩减应该和步长 α 以及方向导数 ∇f(xk)^Tpk 达成一定以上的比例。这个条件叫做足量衰减条件（sufficient decrease condition） 或者 Armijo 条件（Armijo condition）。
上图的横轴是 {xk+αpk:α∈R} 的一维直线，实线曲线是目标函数 f 在这个一维截面上的图像。我们从左侧的红点处出发，虚线表示的是直线 L(xk+αpk)=f(xk)+c1α∇f(xk)^Tpk 的图像，如果 c1=1 的话那么虚线恰恰是曲线在 xk 的切线。稍经分析可以看出，所有曲线低于虚线的位置都满足第一个不等式。实际应用中的 c1 一般设得很小，10^−4 是一个比较常用的值，不过应随应用场景进行调整。
这里可以看出一个问题：起点的附近都小于虚线，没有被不等式排除；但我们并不想选过短的步长，因为这样离极小点依旧很远。因此，Wolfe 条件中有第二个不等式
这个不等式叫做曲率条件（curvature condition），它的意思是落脚点的梯度应该大于一定比例的起始点的梯度。我们使用的向量 pk 使得该方向的梯度 ∇f(xk)^Tpk 小于 0，因此满足不等式的点的梯度应该更缓和（更接近 0），或者是向相反方向的（大于 0）。毕竟，在一个局部的极值点上，函数的梯度必定是 0，所以从一个梯度为负的点出发，我们应该要求梯度变得越来越大，才有可能找到极小点。
上图中，所有梯度大于起始点（也就是下降速度比起始点的下降速度慢）的区域都满足第二个不等式。在应用中，c2 应根据选择 pk 的方法进行选择。在这个示例中，同时满足 Wolfe 条件中两个不等式的区域如下图所示。
寻找一个满足 Wolfe 条件的步长并不是很困难，但确实是比较麻烦。今天就假设我们又笨又懒，只想找一个简单粗暴有效可以完成任务的方法，往下看。
这个算法输出的步长会有足够的下降，并且它保证了这一步不会太短：如果回溯的输出是 αk，那么我们知道 αk/ρ 作为一个步长是太长了，因为它不满足足量下降条件；所以虽然 αk 可能不够精确，但不会太短。
初始的 α¯ 决定了输出步长的上限，用梯度下降或者牛顿方法时都可以将它设为 α¯=1。另外一个参数 ρ 的选择面临一个权衡：如果 ρ 接近 0 的话，回溯算法会在更少的循环中完成，但整体的优化搜索收敛得会更慢；如果 ρ 接近 1 则正相反。一般来说，选择的方向越精确就可以把 ρ 设得越大。
回溯算法对于牛顿方向是一个非常好用的步长计算方法，但对于一些文中没有提到方向（比如拟牛顿(quasi-Newton)和共轭梯度(conjugate gradient)）就不太好用了，不过，这些都是以后的话题了。
一个完整的线搜索算法
正如之前所说，线搜索方法是由一个选择方向的算法和一个寻找步长的算法组成的，在有了这两个主要成分之后就可以拼凑起来。给定一个函数 f 和起始点 x0，我们计算从 x0 出发的下降方向 p0，再计算相对应的步长 α0，并得到一个新的点 x1=x0+α0p0。再从 x1 开始，计算 x2=x1+α1p1。如此重复，得到一个序列 x3,x4,x5,…，并且知道（或者不知道但假设）这个序列会收敛于一个局部极小点。那么问题来了，在绝大多数情况下我们不可能得到确切的极小点，那么我们该在什么时候终止迭代的过程呢？
一般用到的终止条件有两个：迭代次数和函数误差。迭代次数很好理解，我们设一个次数 K，那么在计算出 xK 后就终止计算，并且以 xK 作为极小点的估测；这是一个以运算时间作为标准的终止条件。与之相对的，函数误差是一个计算精度为标准的条件，我们设定一个 ε>0，并且假设序列 x0,x1,… 收敛于某个点 x∗∈R^n，希望在 |f(xk)−f(x∗)|<ε 时中止计算。不过这并不现实，虽然 f(x∗) 比 x∗ 更好找，但很多时候我们还是很难把它计算出来；一个可以替代的条件是，当出现 |f(xk)−f(xk−1)| 的情况时终止计算，并输出 xk。精度和时间的终止条件可以同时使用。
所有部件都已齐全，一个完整的线搜索的优化算法如下：
结语
无约束的非线性规划问题有很多在实际场景中的应用，但更多的应用还是在于有约束的规划问题。比如在我们都非常关心的资产配置问题中，如果用 xi 代表在金融资产 i 上的分配权重，我们会要求资产配置的总和是 1，也就是 
；我们可能要求不能做空，那么有 xi≥0；也许又要求任何一种资产的权重都不超过总资产的三分之一，于是又有 xi≤1/3。这些要求让优化问题变得更困难但也更有趣，有时我们需要为一组特定的约束条件专门研究一套算法来解决。一切才刚刚开始，请读者期尽情待量化课堂未来的文章。
点击『阅读原文』，到JoinQuant社区交流讨论。
长按指纹，关注JoinQuant