遗传算法已被广泛应用于组合优化、机器学习、信号处理、自适应控制和人工生命等领域。例如,在组合优化问题中,遗传算法可以用于求解旅行商问题、背包问题等;在机器学习领域,遗传算法可以用于优化神经网络的权重和阈值等参数。

As shown below👇
遗传算法介绍
算法基本原理
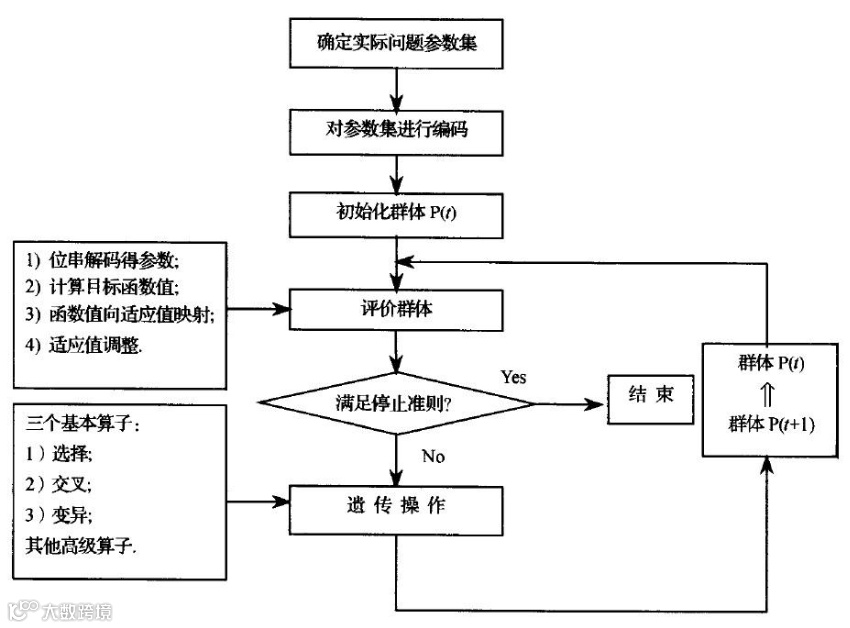
遗传算法的基本原理借鉴了自然界中的生物进化过程,主要包括选择(Selection)、交叉(Crossover)和变异(Mutation)三大操作。这些操作模拟了自然选择和遗传变异的过程,帮助算法在搜索空间中逐步逼近最优解。通过模拟自然进化过程来搜索最优解的优化算法,其基本原理是将问题的解表示为一个染色体,然后通过选择、交叉和变异等操作来优化染色体。步骤如下:
1、参数及种群初始化:设置种群大小、最大迭代次数、搜索空间维度等,并随机初始化种群。
2、解码与适应度计算:对种群中的个体进行解码并计算适应度值。
3、选择、交叉与变异:选择父代个体,进行交叉和变异操作,生成子代。
4、结束条件判断:检查是否满足结束条件,如达到最大迭代次数或找到满意的解。
5、输出最优解:输出全局最优解。
算法举例
旅行商问题(TSP)
旅行商问题是一个经典的组合优化问题,它要求一个旅行商从一个城市出发,访问一系列给定的城市各一次,并最终返回出发城市,目标是找到一条路径使得总旅行距离最短。
将每个城市的访问顺序编码为一个染色体,例如,如果城市集合为{A, B, C, D},则一个可能的染色体为“ABCD”,表示旅行商按照A->B->C->D的顺序访问城市。
% 假设城市坐标矩阵C已给出% C = [x1, y1; x2, y2; ...; xn, yn]; % 其中(xi, yi)是第i个城市的坐标% 初始化参数popsize = 100; % 种群大小maxgen = 100; % 最大迭代次数pc = 0.8; % 交叉概率pm = 0.1; % 变异概率% 初始化种群(随机生成城市访问顺序)population = randi(size(C, 1), popsize, size(C, 1));% 迭代过程for gen = 1:maxgen% 评估适应度(计算总旅行距离)fitness = zeros(popsize, 1);for i = 1:popsize% 计算第i个染色体的适应度(这里需要实现距离计算逻辑)% ...fitness(i) = % 计算得到的总距离(越小越好)end% 选择操作% ...(实现选择逻辑,如轮盘赌选择)% 交叉操作% ...(实现交叉逻辑,如单点交叉)% 变异操作% ...(实现变异逻辑,如随机改变城市顺序)% 更新种群% ...(将新生成的染色体替换原种群中的染色体)end% 输出最优解[minFitness, bestIdx] = min(fitness);bestSolution = population(bestIdx, :);disp('最优解(城市访问顺序):');disp(bestSolution);disp('最短路径总距离:');disp(minFitness);
遗传算法是一种模拟自然进化过程的搜索算法,具有全局搜索能力、隐并行性、自适应性和鲁棒性等特点,在多个领域都有广泛的应用前景。



