超材料通常是通过在整个空间区域中以规则阵列的形式排列一组小散射体或孔径来设计的,从而获得一些理想的体电磁行为。在过去的二十年,超材料已经从简单的理论概念转变为一个具有开发和市场化应用的领域。三维超材料可以通过在表面或界面处将电小散射体或孔排列成二维图案来扩展。这种超材料的表面版本被命名为超表面。对于许多应用,可以使用超表面代替超材料。超表面的优点是比全三维超材料结构占用更少的物理空间。因此,超表面提供了损耗较小的结构的可能性。
超表面在电磁学中具有广泛的潜在应用(从低微波到光学频率),包括:(1)可控的“智能”表面,(2)小型化腔体谐振器,(3)新型波导结构,(4)与角度无关的表面,(5)吸收体,(6)生物医学设备,(7)太赫兹开关和(8)流体可调频率捷变材料。


As shown below👇
超表面与频率选择表面(尺寸与波长的比较)
了解周期性复合材料在不同频率范围或不同长度尺度上的电磁行为是很重要的。这种复合材料的行为可以分为三个不同的区域(见图),每个区域都有不同的行为。
对于三维体材料,区域1对应于准静态区域。这意味着低频率:更具体的是,波长远远大于结构周期的频率(即组成复合介质的散射体的周期性)。这些散射体可能会诱导或永久的偶极矩,就像经典材料中的原子或分子一样。在该区域,使用经典的混合公式来获得等效的有效材料性质(介电常数ε,磁导率μ)。有效介质特性的测定和对主体材料中嵌入的夹杂物的电磁响应的建模是一个有着悠久历史的问题,可以追溯到麦克斯韦和瑞利。

当波长变得与结构的周期相当或小于结构的周期时,场不再“看到”复合材料作为有效介质。这对应于图中的区域 3。在这些频率下,存在更复杂的场行为,必须使用更复杂的技术来分析电磁场与复合周期结构的相互作用(即全波方法)。对此的经典分析方法是Floquet-Bloch模式展开,其中场被扩展为在各个方向传播的平面波的无限和。当波长接近周期时,必须考虑高阶Floquet-Bloch模式。然后,这些高阶模式会干扰通过复合材料传播的基波,我们称复合材料为该频率范围内的光子带隙或电磁带隙材料。我们可以说在这种情况下,材料表现出阵列或晶格色散。在某些频率下,光子带隙和电磁带隙结构会阻挡电磁波在材料中的传播。发生这种情况的频带称为阻带。在其他频率下,周期性结构允许能量通过结构传播:这些频带被称为通带。布拉格散射等现象与该频率区域有关,是许多实际应用的基础。
图中的区域 2 对应于一个区域,其中结构的周期与波长相比仍然很小,但单个散射体的设计方式(通过其形状或本构特性)使得散射体本身可以共振。当这种情况发生时,一类新的人造材料(超材料)就实现了,从而使自然界中不常见的广泛独特行为(例如,双负或近零指数材料)成为可能。区域 2,散射共振的地方(但不是晶格,就像区域 3 中的情况一样),就是我们称我们的介质为超材料的地方。介质在这里是色散的,但我们仍然可以用有效参数来表征其电磁行为ε和μ.
超表面的表征
超表面有效介电常数和磁导率(以及折射率)没有唯一定义。
提出了一种基于反射反转和传输系数的独特表征方法。下面给出了TE极化平面波的反射系数R和透射系数T。

一旦获得了反射系数和透射系数(通过测量或数值计算),就可以确定表面磁化率(surface susceptibilities)。
对于te极化波,三种未知的表面磁化率由以下方法确定,
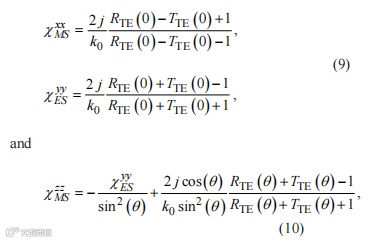
在二维材料中可将它们插入到Clausius-Mossottii关系中,以获得通过在第三维中堆叠这些超膜来实现的超材料的有效介电常数和磁导率。
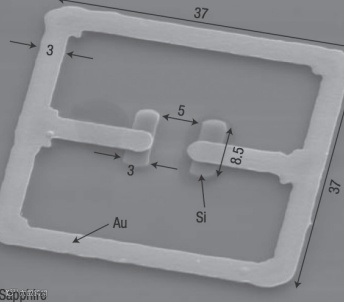
超表面提供了块状三维超材料的替代方案。由于超表面结构的二维性质,它们占用的物理空间较少,损耗也较小。虽然有效性能模型适用于三维超材料,但表征超表面/超膜的更合适的方法是它们的有效表面电化率和磁化率,其中这些表面磁化率与组成超表面的散射体有关。




