
- George Harrison, 1949
衍射光栅通过自身的重复结构分离不同波长的光,根据工作方式可分为透射和反射两种类型。在入射角θi = 0°时,所有衍射光栅满足以下光栅方程:

α表示光栅的刻槽间距,也叫光栅常数,λ是波长,θm是相对光栅表面法线的m级衍射角。根据光栅方程,对于给定的衍射级次,不同波长的光具有不同的衍射角,所以白光将形成与角度相关的连续光谱。

准直的超连续激光通过光栅衍射,从中可以看到不同的衍射级次(来源OSA)
透射式光栅的结构和方程如下所示:


如果入射光和衍射光在光栅法线两侧,那么θi和θm都为正;如果在光栅法线同侧,θm必须看作负值。

反射式光栅的结构和方程如下所示:
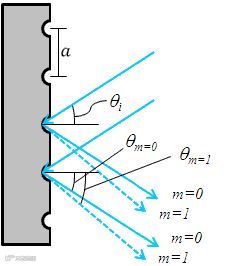

如果入射光和衍射光在光栅法线两侧,那么θi为正,θm为负;如果在光栅法线同侧,两个角度都为正。
闪耀光栅也称为小阶梯光栅,属于特殊的反射或透射光栅,能在特定衍射级次提供最高效率,使得在设计级次上具有大部分光功率,而其它级次尤其是零级功率最低。由于这种设计,闪耀光栅以特定的闪耀波长工作。

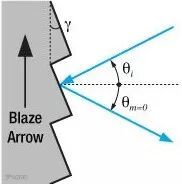
闪耀光栅结构
闪耀光栅的三个重要特征参数是闪耀波长、光栅常数和闪耀角ϒ。ϒ为刻槽面和光栅表面的夹角,也等于两面法线的夹角,详见上图所示。闪耀光栅由于阶梯(锯齿)结构将有一个取决于闪耀角的镜面反射,可以通过改变闪耀角改变衍射效率,先看一个闪耀角变化的仿真。

模拟单色光衍射级次随闪耀角的变化
来源:Bertolotti, 爱克塞特大学
下图展示闪耀光栅的零级反射,以θi入射,以θm反射。根据反射光栅方程,零级条件下的唯一解是θi = -θm,这类似于平面镜反射。
闪耀光栅零级反射
但闪耀光栅在阶梯形刻槽面的反射不同于零级反射,如左下图所示。假设在刻槽面的反射角相对光栅法线为θr,如果θr和θi在光栅法线同侧取负值。通过简单的几何变换可得:

右下图为θi = 0°的特殊情况,此时零级反射也处于0°。我们可以推出两倍闪耀角处的光栅方程(右下图):


从阶梯刻槽面的反射

从光栅表面正入射
Littrow配置角度(θL)是指光栅效率最高时的入射角,这个角度在单色仪和光谱仪中非常重要。在此配置中,入射角等于衍射角且m大于0,所以:


Littrow配置:θL = ϒ
θL取决于最强级次(m = 1)、设计波长λD和光栅常数α,可以看到在设计波长处Littrow角等于闪耀角ϒ。
在正入射条件下,随着衍射级次变高,与波长相关的角度距离变大。使用高级次衍射图案相比低级次有两个缺点:衍射效率更低、自由光谱范围更小。
低衍射效率问题可以通过使用中阶梯光栅解决,这种光栅具有极大闪耀角和较低的刻槽密度。大闪耀角将能量集中到较高级次衍射中。解决第二个问题的办法是在中阶梯光栅后面加一个光学元件控制波长/级次,比如光栅、色散棱镜或其它色散元件。
虽然闪耀光栅在设计波长下具有很高的效率,但其缺点是周期误差较大、散射较高,这将降低测量灵敏度。全息光栅能够降低或消除周期误差,不过效率相比闪耀光栅更低。
全息光栅也是从母光栅复制,过程和刻划光栅相似。制备母全息光栅一般是使用两束干涉激光在光敏材料进行光刻。干涉图案在表面上刻出周期图案,通过物理或化学处理产生正弦表面结构。下图展示了这样一种全息光栅结构。

选择光栅需要考虑多种因素,比如:
-
效率:刻划光栅一般比全息光栅效率更高。全息光栅效率相对更低,但波长范围更宽。可能需要高效率刻划光栅的应用包括荧光激发和其它光诱导反应等。 -
闪耀波长:刻划光栅具有锯齿形结构,所以在闪耀波长附近提供高峰值效率。全息光栅闪耀更难,一般具有正弦表面结构,所以在设计波长附近形成强度较弱的峰。 -
杂散光:全息光栅比刻划光栅杂散光更少。刻划光栅的周期误差更多,全息光栅几乎没有误差,所以杂散光更少。对于要求高信噪比的应用,比如拉曼光谱,适合使用全息光栅。 -
分辨力:光栅分辨力衡量其分离两个波长的能力,通过R = λ/Δλ = m*N定义,其中Δλ是可分辨波长差,m是衍射级次,N是被照刻槽数。中阶梯光栅由于密度低因此分辨更高。
衍射光栅表面容易因指纹、气溶胶、湿气或者与任何粗糙材料的轻微接触受损。在必要时操作光栅,只能从边缘拿。佩戴乳胶手套防止手指油渍污染光栅表面。溶液很可能损伤光栅表面。清洁光栅只能使用清洁的干燥空气或氮气吹扫灰尘。光栅表面的刮痕或其它微小的瑕疵一般不会影响性能,并不视为缺陷。
文章转自:Thorlabs索雷博
延伸阅读:
微知识 | 激光器线宽的表征方式——kHz与nm换算关系
扫码关注我们
本文注明来源为其他媒体或网站的文/图等稿件均为转载,如涉及版权等问题,请作者在20个工作日之内联系我们,我们将协调给予处理。最终解释权归光电汇所有。
本文版权所有,
公众号如需转载
请联系oepn@siom.ac.cn
我知道你在看哟





