
概念与定义

2.核心思路
检验统计量 t 值计算公式:

其中:
xˉ:样本均值
s:样本标准差
n:样本量
p 值基于 t 分布和自由度 n−1 计算,若 p < 0.05,则认为样本均值与理论值存在显著差异。
适用场景:
数值型变量的均值检验:如检验某产品平均重量是否为 100g,或某班级平均分是否达到 80 分。
样本量较小:适合样本量较小(如 < 30)或数据偏离正态分布的情况(需结合非参数检验)。
定量数据:仅适用于数值型(连续型)数据,分类或文本数据需转换为数值或更换检验方法。
1.选择分析方法
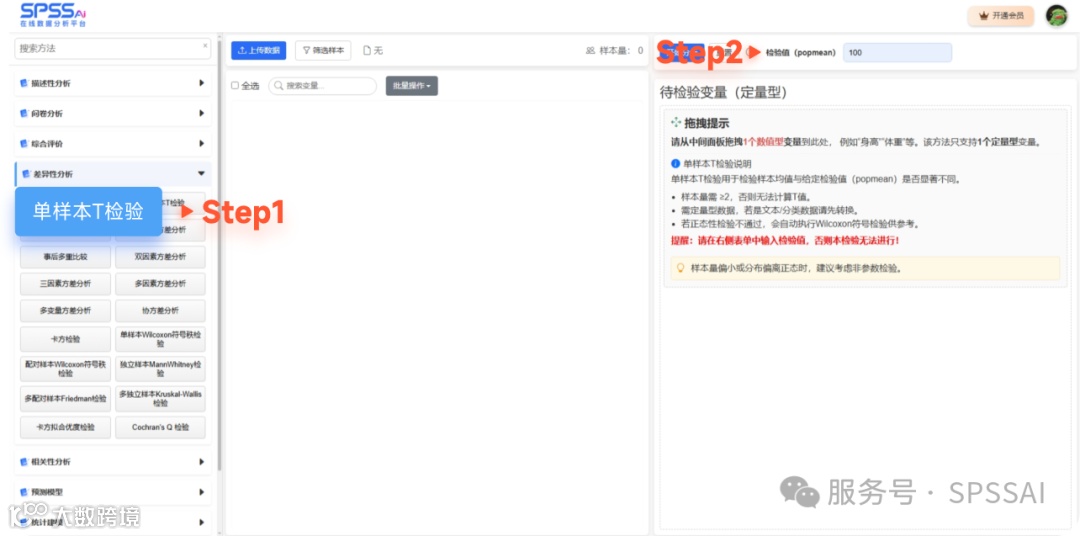
step1.登录SPSSAI数据分析系统,在左侧菜单或主页面选择「差异性分析」下的「单样本T检验」。
step2.参数设定:在右侧面板设置「检验值(popmean)」,输入理论均值(如 100)
2.上传分析数据
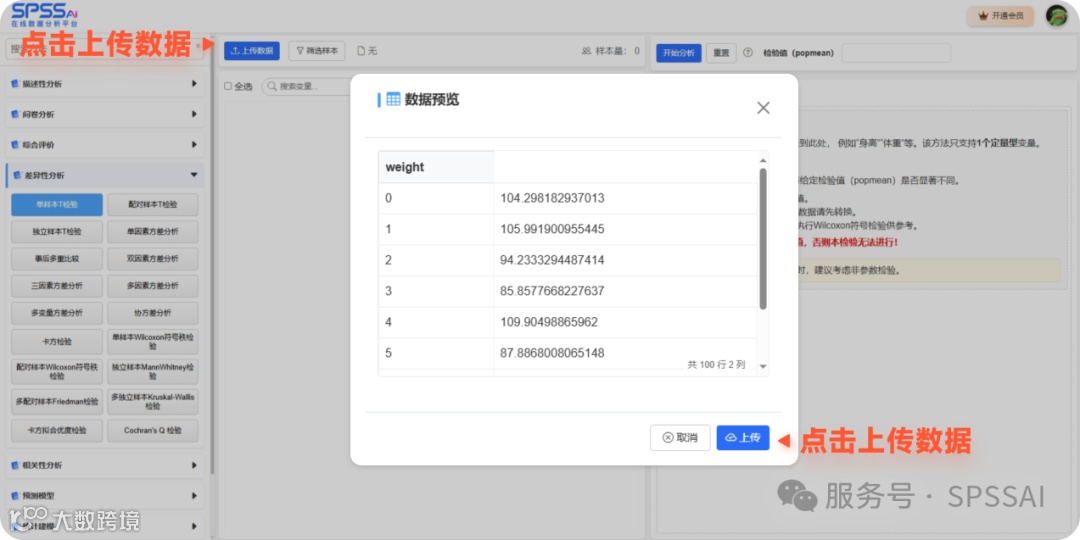
step1.支持XLSX、CSV、SAV、DTA、SAS7BDAT格式,不支持老式.xls。文件第一行为列名,便于系统识别。
step2.点击后,预览数据数据无误点击上传。
变量类型:
仅支持数值型变量,分类或文本数据需先转换。
样本量要求至少 2 条有效记录。
3.数据拖拽开始分析
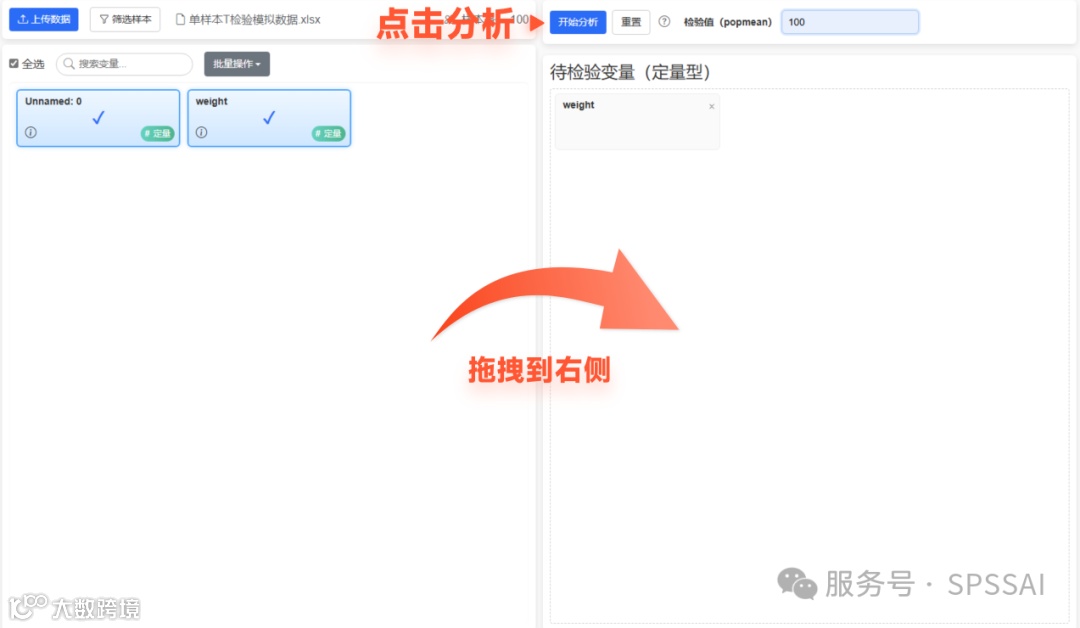
step1.在中间面板选中对应列,拖拽至右侧面板。
step2.完成拖拽后,点击「开始分析」,系统生成唯一报告 ID 并跳转至报告页面。
变量类要求:
在中间面板选择 1 个定量型变量(如「身高」或「销售额」)。
拖拽至右侧「待检验变量(定量型)」区域。
若拖拽多列或非数值字段,系统会提示报错。

输出结果一:描述性统计
样本量:有效观测值数量。
均值:样本均值,与理论值(popmean)进行比较。
标准差:样本数据的离散程度。
偏度与峰度:评估数据分布形态(偏度 > 2 或 < -2 表示偏离正态)。

输出结果二:正态性检验
Shapiro-Wilk (S-W) 和 Kolmogorov-Smirnov (K-S) 检验:
p ≥ 0.05:数据未显著偏离正态,可使用 T 检验。
p < 0.05:数据偏离正态,需结合非参数检验(如 Wilcoxon 符号检验)。

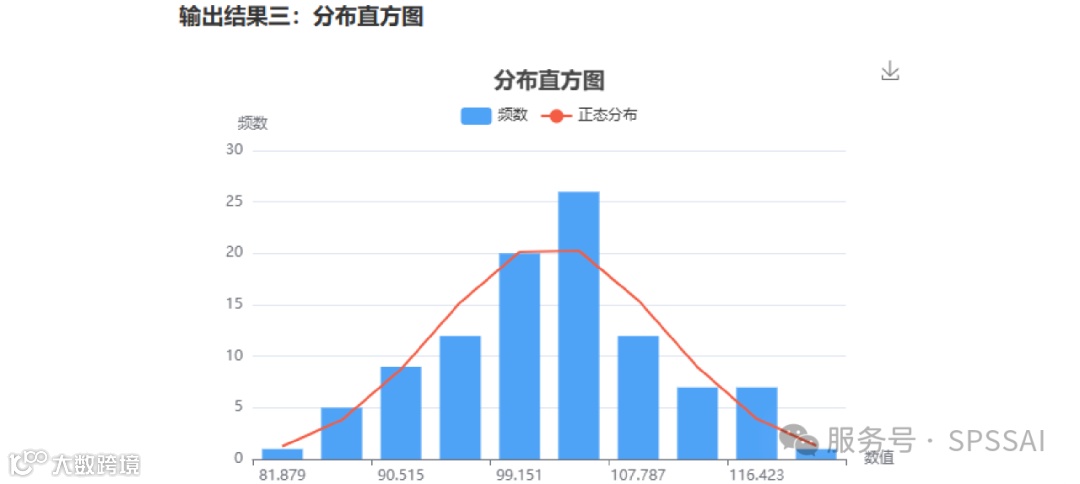
输出结果三:分布可视化
直方图:显示数据分布形态,与理论正态曲线对比。
Q-Q 图:散点越接近对角线,分布越接近正态。

输出结果四:单样本T检验结果
t 值与p值:p < 0.05 表示样本均值与理论值存在显著差异。
95% 置信区间:样本均值的可信区间。
Cohen's d 效应量:衡量差异大小(0.2=小,0.5=中,0.8=大)。
非参数检验(Wilcoxon 符号检验):当数据偏离正态时提供参考。

输出结果五:后续改进建议
若需比较多个组,可使用 ANOVA 或独立样本 T 检验。
若需深入分析,可尝试回归分析或多元统计方法。

数据质量:缺失值或异常值可能影响结果,建议先进行数据清洗。
正态性假设:样本量较大(> 30)时,T 检验对正态性要求相对宽松。
样本规模:样本量 < 30 时,p 值稳定性较弱,需谨慎解释。
检验值合理性:理论值需基于业务背景合理设置。
结论解释:结合效应量(Cohen's d)评估差异的实际意义,而非单纯依赖 p 值。
后续处理:若需比较多个样本间的差异,可使用独立样本 T 检验或单因素 ANOVA。
一、单样本 t 检验
单样本 t 检验用于判断样本均值与已知总体均值之间的差异是否显著。
二、核心步骤
1. 假设设定
零假设(H₀):样本均值等于总体均值(Xˉ=μ)。
备择假设(H₁):样本均值不等于总体均值(Xˉ=μ)。
2. 抽样分布
样本数据近似正态分布,满足 t 分布条件。
3. 检验方向
备择假设为双尾检验(样本均值可能大于或小于总体均值)。
4. 计算 t 值
t 值公式为:

其中:
Xˉ 为样本均值;
μ 为总体均值;
n 为样本量;
样本标准差:
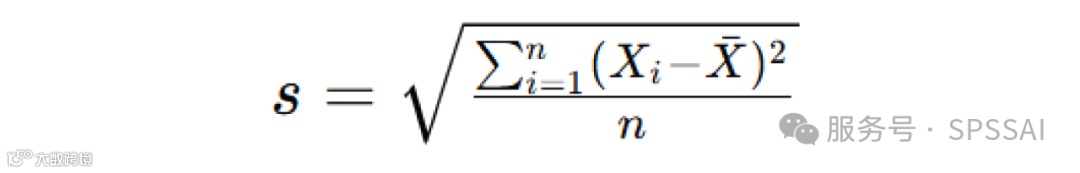
5. 计算 p 值
p 值表示在零假设成立时,观察到当前样本或更极端样本的概率。自由度为 n−1。
6. 置信区间
置信区间公式为:
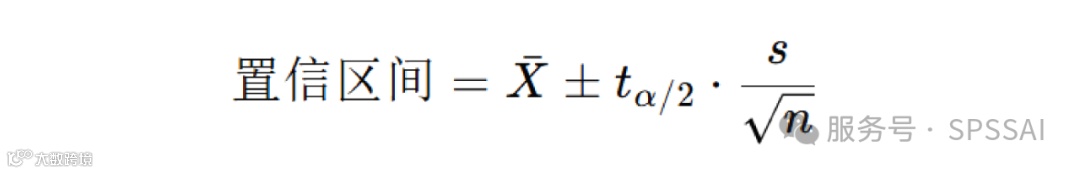
三、结论
若 p 值小于显著性水平(如 0.05),拒绝零假设,认为样本均值与总体均值差异显著。
若 p 值大于显著性水平,无法拒绝零假设,认为差异不显著。
# 参考文献
Student. The Probable Error of a Mean. Biometrika, 1908, 6 (1): 1–25.
Cohen, Jacob. Statistical Power Analysis for the Behavioral Sciences. 2nd ed. Hillsdale, NJ: Lawrence Erlbaum Associates, 1988.
Field, Andy. Discovering Statistics Using IBM SPSS Statistics. 5th ed. London: SAGE Publications, 2018.
Cumming, Geoff. Understanding the New Statistics: Effect Sizes, Confidence Intervals, and Meta-Analysis. New York: Routledge, 2012.
Rosenthal, Robert, and John E. Rosnow. Essential of Behavioral Research: Methods and Data Analysis. 3rd ed. New York: McGraw-Hill, 2008








