
生成式 AI 的浪潮中,图像生成模型一直是研究热点。扩散模型(Diffusion Models)和流匹配(Flow Matching)虽能生成高质量图像,但动辄 50 步以上的采样过程,让高维度数据(比如高清图像、视频)的生成效率大打折扣。能否用单步 / 少步采样,就生成媲美多步模型的高质量图像?近日,Luma AI 团队提出的 Terminal Velocity Matching(TVM)框架,给出了惊艳的答案 —— 它不仅实现了单步生成的 SOTA 性能,还兼具理论保证与工程落地性。今天我们就深度拆解这篇刷新少步生成模型天花板的论文!

研究背景:少步生成模型的核心痛点
当前主流的生成模型(扩散、流匹配)依赖 ODE 求解器完成采样,多步操作导致推理效率极低。为了实现单 / 少步生成,现有方法(如 Consistency Models、MeanFlow)要么缺乏分布匹配的理论保证,要么需要多粒子训练限制可扩展性。而 TVM 的核心创新,就是从 “终端速度匹配” 切入,既解决了理论支撑问题,又实现了单阶段训练的高效性。
(配图:论文 Figure 2)

理论突破:2-Wasserstein 距离的明确上界
理论层面,TVM 的关键突破是证明了:当模型满足 Lipschitz 连续时,其训练目标能为数据分布与模型分布之间的 2-Wasserstein 距离提供上界。这是首次为单步生成模型提供明确的分布匹配理论保证,且无需像 Inductive Moment Matching(IMM)那样依赖多粒子训练,大幅提升了模型的可扩展性。
工程落地:攻克三大核心挑战
理论落地需要解决实际问题,TVM 团队针对性攻克了三大工程挑战:
-
Lipschitz 连续性缺失问题:现有扩散 Transformer(DiT)不满足 Lipschitz 连续,会导致训练不稳定(激活爆炸)。TVM 通过极简架构修改 —— 用 RMSNorm 替代 LayerNorm、对 QK 归一化采用 RMSNorm、对时间嵌入调制参数做归一化,实现了半 Lipschitz 控制,让激活值保持稳定。 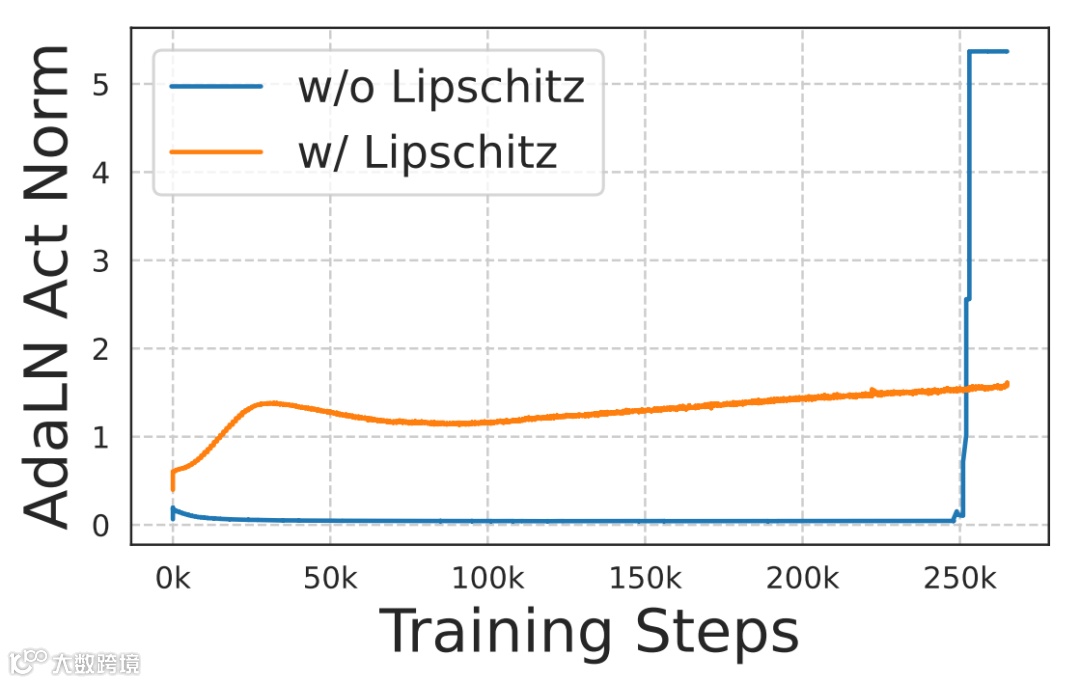
-
高效 Flash Attention JVP 实现:TVM 的训练目标需要计算 Jacobian-Vector Product(JVP)的反向传播,而传统 Flash Attention 对 JVP 支持不足。团队自研的 Flash Attention 内核,融合 JVP 与前向传播,相比标准 PyTorch 操作提速 65%,还大幅降低内存占用。 -
优化器与参数化调优:针对 JVP 带来的损失波动,将 AdamW 的 β2 从 0.999 调整为 0.95,让梯度二阶矩更新更快,损失曲线更平滑;同时设计缩放参数化,让模型输出随 CFG 权重自然缩放,避免梯度爆炸。

实验结果:刷新 ImageNet 少步生成 SOTA
TVM 在 ImageNet 数据集上的实验结果堪称硬核,全面刷新单 / 少步生成模型的性能上限:
ImageNet-256×256:单步(1-NFE)FID 达 3.29(超越 MeanFlow 的 3.43),4 步(4-NFE)FID 仅 1.99,超过 500 步扩散基线(DiT 的 2.27);
ImageNet-512×512:单步 FID 4.32,4 步 FID 2.94,超越 sCT、MeanFlow 等主流方法,且匹配 500 步 DiT 基线性能。
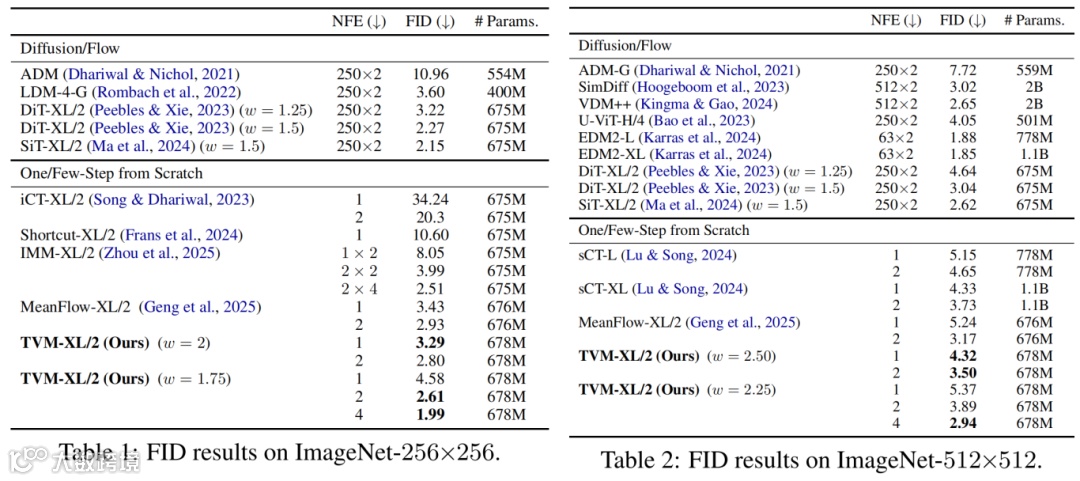
Table 1(ImageNet-256×256 FID 结果)和 Table 2(ImageNet-512×512 FID 结果)量化验证了 TVM 的性能优势。

Figure 6 展示了 TVM 在 ImageNet-256/512 上的 1-NFE 生成样本,视觉效果媲美多步模型。
此外,TVM 的训练优势也十分显著:单样本即可完成损失计算(适配大模型训练限制)、随机 CFG 训练时梯度 / 速度范数更稳定、无需课程学习 / 损失修改等额外策略,设计简洁易扩展。

总结:理论与实践兼具的少步生成新范式
TVM 以 “终端速度匹配” 为核心,首次为单 / 少步生成模型提供了 2-Wasserstein 距离的理论上界,同时通过极简的架构修改、高效的内核实现和优化策略,解决了工程落地的关键问题。它不仅在 ImageNet 上实现了 SOTA 的单 / 少步生成性能,还为高维度、高分辨率生成模型的高效推理提供了全新思路 —— 兼顾理论严谨性与实践可用性,这正是高质量学术研究的典范。
论文出处



