
01
引言
今天我们将深入探讨另一种基本的机器学习算法:逻辑回归。在前两篇文章中,我们使用线性回归和梯度下降法帮助我们的朋友马克确定了他 2400 平方英尺房子的理想售价。
最近马克再次向我们求助。他住在一个高档社区,他认为低于一定面积的房子是卖不出去的,他担心自己的房子也卖不出去。他请我们帮他确定他的房子卖出的可能性有多大。这就是逻辑回归算法的作用所在。
闲话少说,我们直接开始吧!
02
问题引入
逻辑回归是一种预测二元结果概率的算法,例如房屋是否会售出。与线性回归不同,逻辑回归使用 0% 到 100% 的范围预测概率。请注意线性回归模型和逻辑回归模型预测结果的区别:

让我们通过确定不同面积房屋的销售概率来深入探讨逻辑回归的工作原理。我们再次开始收集马克所在社区的房屋面积数据,并查看它们是否售出。

现在,让我们来绘制这些点:

与其用二进制输出来表示绘图结果,不如用概率来表示,因为我们要预测的就是概率。
我们将 100% 的概率表示为 1,将 0% 的概率表示为 0

03
线性回归的问题
在=在上一篇文章中,我们了解了线性回归及其根据数据拟合直线的能力。但是,对于我们需要输出概率的问题,线性回归是否有效呢?让我们通过尝试使用线性回归拟合一条直线来找出答案。


根据这条直线,我们可以看出,面积略低于 2700 平方英尺的房屋被售出的概率为 100%:

而面积为2200 平方英尺的房子被卖出的几率预计为 0%:

据预测,面积2300 平方英尺的房屋售出的可能性约为 20%,如下:

好吧,到目前为止一切顺利。但如果我们的房子面积是 2800 平方英尺呢?

嗯......概率超过 100%是什么意思?这么大的房子,预测卖出的概率是 150%吗?
多少有点奇怪。那 2100 平方英尺的房子呢?

很明显,我们遇到了一个问题,因为面积为 2100 平方英尺的房屋的预测概率似乎是负数。这肯定是不合理的,也说明使用标准线性回归线存在问题。
04
引入sigmoid函数
我们知道,概率的取值范围是从 0 到 1,我们不能超出这个范围。因此,我们需要找到一种方法,将预测输出限制在这个范围内。
为了解决这个问题,我们可以将我们的线性回归方程通过一个超酷的机器学习函数,称为sigmoid 函数。我们将 z 值(其中 z = β₀ + β₁size)输入该函数中,如下:

然后就会出现一个看起来很华丽的新方程,可以满足我们的概率限制。
我们可以用一种更数学化的方式来表示 sigmoid 函数:

如果我们将其绘制出来,就会发现 sigmoid 函数将直线挤压成了一条 s 形曲线,并将其取值限制在 0 和 1 之间。

05
逻辑回归思想
与线性回归类似,我们将利用代价函数和梯度下降算法来获取这些系数的合适值。但关键区别在于,我们不会使用线性回归中使用的 MSE 成本函数。相反,我们将使用一种不同的成本函数,称为对数损失,我们将在下文中详细探讨。
假设我们使用梯度下降法和对数损失成本法(使用这些步骤)发现最优值为 β₀ = -120.6 和 β₁ = 0.051,那么我们的预测概率方程将是:
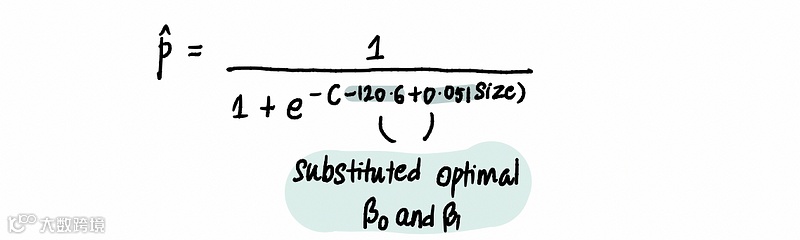


为了开发分类算法,我们需要定义一个概率阈值。这个概率阈值将预测概率分为两类:"是,房子会卖掉 "和 "否,房子不会卖掉"。通常情况下,阈值为 50%(或 0.5)。
如果房屋大小作为输入预测出概率高于 50%,则会被归类为 "会出售",如果低于 50%,则会被归类为 "不会出售"。

06
成本损失函数


为了分解对数损失成本函数,我们需要分别定义房屋实际售出(y=1)和未售出(y=0)时的成本。
如果 y = 1,而我们预测为 1(即售出的可能性为 100%),则不会受到惩罚。但是,如果我们预测的是 0(即没有售出的可能性为 0%),那么我们就会受到严重惩罚。





07
总结
本文重点介绍了如何利用逻辑回归算法来求解机器学习中分类问题,并给出了详细的图例说明。
您学废了吗?
点击上方小卡片关注我
添加个人微信,进专属粉丝群!



