一文弄懂主成分分析PCA算法

主成分分析（PCA）是数据科学中不可或缺的可视化和降维工具，但大家往往被埋没在复杂的数学公式中。至少可以说，我很难理解其中的原因，因此很难欣赏到它的全部魅力。今天我们就用大白话来讲解下主成分分析吧！

闲话少说，我们直接开始吧！

 什么是PCA ?

主成分分析 (PCA) 是一种将高维度数据转换为低维度数据的技术，同时保留尽可能多的信息。

原始三维数据集。红色、蓝色和绿色箭头分别代表第一、第二和第三主成分的方向

PCA 从三维缩减到二维后的散点图

我喜欢把 PCA 比作写一本书的摘要。花时间读完一本长达 1000 页的书是一种奢侈，很少有人能负担得起。如果我们能用两三页纸就概括出最重要的内容，让最忙碌的人也能轻松消化这些信息，岂不更好？在这个过程中，我们可能会丢失一些信息，但嘿嘿，至少我们得到了全貌。

这是一个分两步走的过程。如果我们没有阅读或理解书的内容，就无法写出书的摘要。PCA 的工作原理也是如此 -- 理解，然后总结。

人类通过语言表达来理解故事书的含义。不幸的是，PCA 不会说英语。它必须通过自己喜欢的语言--数学，在我们的数据中寻找意义。那么我们能否用数学方法量化数据中蕴含的信息量？嗯，方差是可以的。数据方差越大，说明其包含信息越多。反之亦然。

对于大多数人来说，方差并不是一个陌生的词汇。我们在高中就学过，方差衡量的是每个点与平均值的平均差异程度。

方差计算公式

但方差具体有什么意义呢？我们来看个例子，假设我们正在和朋友玩猜谜游戏。游戏很简单。我们的朋友会遮住他们的脸，我们只需要根据他们的身高猜出谁是谁。作为好朋友，我们会记住每个人的身高。

记忆中朋友们的高度

我先来。

三个一模一样的朋友的背影，我们需要根据他们的身高差异来识别他们。

毫无疑问，我们可以推断出来A 是Chris，B 是Alex，C 是Ben。现在，让我们来猜一猜另一组朋友。

我们朋友的另一组身高，让我们铭记于心

接着，轮到你来猜了。

三位身高相仿的朋友的剪影，我们需要确认他们的身份。

你能猜出谁是谁吗？当他们身高非常相似时，就很难猜了。上个例子中，我们不难将 185 厘米的人与 160 厘米和 145 厘米的人区分开来，因为他们的身高差别很大。

同样，当我们的数据方差越大，它所包含的信息就越多。这就是为什么我们总能在同一句话中听到 PCA 和最大方差。我想引用维基百科中的一个片段来正式说明这一点。

PCA 被定义为一种正交线性变换，它将数据转换到一个新的坐标系中，使数据的某个标量投影的最大方差位于第一个坐标上（称为第一个主成分），第二个最大方差位于第二个坐标上，以此类推。

在 PCA 看来，方差是量化数据信息量的一种客观的数学方法。也就是说，差异就是信息。

为了让大家明白方差就是信息，我提议再进行一次猜拳比赛，只不过这次我们要根据身高和体重来猜出谁是谁。

我们的数据如下：

同一组朋友及其各自的身高和体重

一开始，我们只有身高。现在，我们朋友的数据量基本上翻了一番。这会改变大家的猜测策略吗？这是进入下一节的一个很好的小插曲--PCA 如何概括我们的数据，或者更准确地说，如何降低维度。

上述这个例子中，就我个人而言，体重差异非常小（又称小方差），根本无法帮助我区分我们的朋友。我还是主要依靠身高来进行猜测。直观地来说，我们只是将数据从 2 维减少到了 1 维。这样做的目的是，我们可以有选择地保留方差较大的变量，而遗忘方差较小的变量。

但是，如果身高和体重的方差相同呢？这是否意味着我们不能再降低这个数据集的维度？我想用一个样本数据集来说明这个问题。

虚线表示身高和体重的方差

在这种情况下，我们很难选择要删除的变量。如果我删除其中任何一个变量，就等于删除了一半的信息。那么两个都能留下吗？也许，只是看问题的角度不同。

换个角度看问题

最好的故事书总是有隐藏的主题，这些主题不是写出来的，而是隐含的。单独阅读每一章是没有意义的。但如果我们读完所有章节，就会有足够的背景让我们把谜题拼凑起来--潜在的情节就会浮现出来。

到目前为止，我们只是单独研究身高和体重的差异。与其局限于选择其中一个，为什么不把它们结合起来呢？

虚线表示最大方差的方向

为了表示这两条线，PCA 将身高和体重结合起来，创建两个全新的变量。它可以是 30% 的身高和 70% 的体重，或者是 87.2% 的身高和 13.8% 的体重，也可以是任何其他组合，这取决于我们所掌握的数据。

这两个新变量被称为第一主成分（PC1）和第二主成分（PC2）。我们可以分别使用 PC1 和 PC2，而不是在两个坐标轴上使用身高和体重。

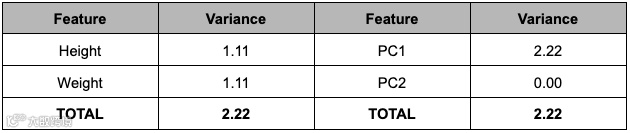
为进行公平比较，所有变量均标准化为同一量纲

仅PC1 就能捕捉到身高和体重的总方差。由于 PC1 包含了所有信息，大家已经知道了其中的奥秘--我们可以很放心地移除 PC2，并知道我们的新数据仍能代表原始数据。

在实际数据中，我们通常不会得到一个能捕捉到 100%方差的主成分。进行 PCA 分析会得到 N 个主成分，其中 N 等于原始数据的维度。一般来说，我们会从这个主成分列表中选择最少的主成分，以解释最多的原始数据。

Scree Plot 是一个很好的视觉辅助工具，可以帮助我们做出决定。

三维数据集的 Scree Plot 示例

上述条形图显示了每个主成分所解释的方差比例。一方面，叠加的折线图告诉我们 N 个主成分之前解释方差的累积总和。理想情况下，我们希望只用 2 到 3 个主成分就能得到至少 90% 的方差，这样既能保留足够的信息，又能在图表上直观地显示数据。从上述图像上看，我觉得使用 2 个主成分比较合适。

总结

本文重点介绍了主成分分析PCA相关的知识点，通过具体的实际例子来加强大家对其基础知识的理解，希望大家读完后可以有更深刻的认识。

添加个人微信，进专属粉丝群！