NeurIPS 2025｜NS-EGNN：建模现实世界中非平稳动态的等变图网络

导语

在分子运动、蛋白质折叠等物理动力学建模中，图神经网络（GNN）展现出强大潜力。为提升泛化能力，等变GNN（Equivariant GNNs）将平移、旋转等物理对称性作为归纳偏置融入模型。但现有方法普遍忽略物理系统的关键特性——非平稳性（non-stationarity），即系统联合分布在时间上动态变化。

传统处理非平稳时间序列的方法（如数据归一化）会破坏物理系统的对称性假设。为此，本文提出非平稳等变图神经网络（NS-EGNN），首次在严格保持E(3)等变性的前提下建模非平稳物理动力学。

NS-EGNN 的核心设计包括：

1. 采用分块傅里叶变换（Patch Fourier Transform, PFT）提取轨迹中随时间变化的频率信息，该模块输出具备E(3)不变性；
2. 引入一阶与二阶差分操作缓解线性及二次趋势，该操作本身保持E(3)等变性；
3. 通过联合建模动态方差（PFT）与动态均值（差分+NS-Pooling），增强对物理时间依赖性的刻画能力。

实验表明，NS-EGNN 在分子动力学（MD17）、人体运动捕捉（CMU Motion Capture）和蛋白质动力学（AdK）三大任务上全面超越当前SOTA模型。

论文地址：https://openreview.net/pdf?id=0dp90Bq8r8
代码仓库：https://github.com/MaojiWEN/NS-EGNN

现存问题及挑战

精确模拟真实物理动力学对分子动力学、药物发现与蛋白质折叠等领域至关重要。等变图神经网络（EGNNs）因其能编码旋转、平移等基本对称性，已成为主流建模范式，显著提升模型对粒子间相互作用的泛化建模能力。

然而，现有模型仍面临两大关键挑战：

1. 非马尔可夫性（Non-Markovian）：多数模型采用单步帧间预测，仅依赖前一帧状态，而真实物理系统未来状态往往依赖于历史轨迹，而非仅当前时刻；
2. 非平稳性（Non-stationary）：系统统计特性（如均值、方差）随时间演变。例如，分子势能变化导致振动幅度波动；人体运动中速度与生理状态持续动态演化。

经典时间序列稳定化方法（如归一化）在三维坐标空间应用时，会直接破坏E(3)等变性，引发过拟合并损害泛化性能。

（图1：非平稳性与等变性示意图。左侧显示不同时段分子动态的傅里叶频谱（S1, S2）差异显著；右侧表明模型应对旋转/平移后的系统输出一致频率特征。）

NS-EGNN：兼顾非平稳性与等变性的新框架

NS-EGNN 将非平稳性解耦为动态方差与动态均值（趋势）两部分，并分别设计保持对称性的模块进行建模。

（图2：NS-EGNN 整体框架，含不变分块傅里叶变换（PFT）与等变非平稳时序池化（NS-Pooling）两大核心模块。）

不变分块傅里叶变换（PFT）：捕捉动态方差

物理系统振动幅度等动态方差特征在频域具显著表达。

• 全局傅里叶变换隐含平稳性假设，无法刻画时变频谱；
• PFT 采用重叠滑动窗口，对各局部片段独立进行傅里叶变换，获取随时间演化的局部频率信息；
• 所提取的功率谱等特征对E(3)变换具备不变性，可在不破坏物理对称性前提下，向EGNN骨干网络注入时变统计信息。

等变非平稳时序池化（NS-Pooling）：缓解动态均值（趋势）

非平稳性的另一来源是整体漂移等时变均值趋势。

• 受ARIMA启发，NS-Pooling 使用一阶与二阶差分消除线性及二次趋势；
• 对三维坐标X执行差分操作 ΔX_i = X_i(t) − X_i(t−1)，该操作天然满足E(3)等变性；
• 对差分后更平稳的轨迹进行池化预测，最终与EGNN骨干网络协同建模空间关系。

NS-EGNN 是首个端到端处理非平稳物理轨迹、且严格保持E(3)等变性的框架。

实验效果与分析

我们在三类典型物理动力学数据集上验证NS-EGNN性能：MD17（分子动力学）、CMU Motion Capture（人体运动捕捉）和 AdK（蛋白质动力学）。

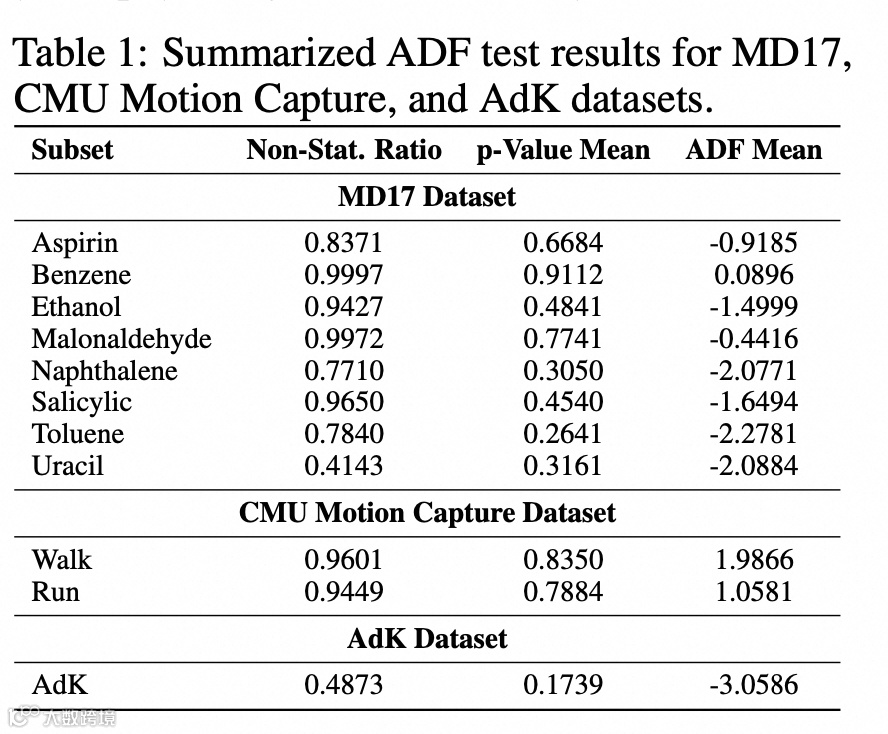
非平稳性验证

通过ADF检验（Augmented Dickey-Fuller test）证实，所有数据集均呈现强非平稳特性（表1）。

性能对比

（表2 & 表3：MD17数据集ADE/FDE误差对比。NS-EGNN在全部分子上取得最低平均位移误差与最终位移误差，显著优于ESTAG、EqMotion等SOTA模型。）

1. 分子动力学（MD17）：相较ESTAG，NS-EGNN在平均位移误差（ADE）提升29.77%，最终位移误差（FDE）提升33.33%；
2. 人体运动捕捉（CMU Motion）：在“行走”与“奔跑”任务中，NS-EGNN预测轨迹（蓝色）更贴近真实值（红色），尤其在复杂关节运动中更平滑、更符合物理规律。

（图3：人体运动捕捉可视化。“行走”与“奔跑”任务中，NS-EGNN（右）轨迹比ESTAG（左）更稳定、更准确。）

消融实验

1. 去除PFT（仅用全局FT）：性能显著下降，证明动态频率建模的必要性；
2. 去除差分（NS-Pooling）：性能大幅下降，验证趋势缓解的关键作用；
3. 去除等变性（改用普通GNN）：模型完全失效，凸显E(3)等变性为物理模拟基石。

总结与未来工作

本文指出真实物理动力学普遍存在非平稳性，而现有等变GNN对此建模存在空白。NS-EGNN通过PFT与NS-Pooling协同机制，在严格保持E(3)等变性的同时实现非平稳轨迹建模，多基准测试结果验证其有效性与泛化能力。

未来工作将探索NS-EGNN在更多场景的应用，并适配小波变换等非平稳分析工具至等变框架。