Methodology for System Complexity Analysis Based on the DIKWP Model (Extended Version)

Yucong Duan

International Standardization Committee of Networked DIKWP for Artificial Intelligence Evaluation(DIKWP-SC)

World Artificial Consciousness CIC(WAC)

World Conference on Artificial Consciousness(WCAC)

(Email: duanyucong@hotmail.com)

introduction

The vigorous development of artificial intelligence and cognitive systems is driving the innovation of algorithmic complexity analysis paradigms. Traditional algorithm complexity studies (such as time complexity, spatial complexity, etc.) mainly serve procedural or functional computing models, emphasizing single-dimensional indicators such as input-output, process control, and resource consumption. Although these classical complexity measures are effective in measuring the performance of algorithms, they cannot directly describe the semantic complexity and cognitive process complexity in the face of intelligent systems with semantic understanding and autonomous cognitive capabilities. For example, the current data-driven large language models (LLMs) have many limitations in terms of data, information, knowledge, intelligence, intent, and their mutual transformation: the lack of explicit characterization of "intent" will lead to incomplete, imprecise and inconsistent semantic content, opaque decision-making process, unpredictable results, and even potential ethical risks. This phenomenon shows that it is difficult to comprehensively measure the source and performance of system complexity in cognitive intelligence systems by relying only on traditional complexity indicators.

In order to solve the above problems, the researchers proposed the DIKWP model, which extends the complexity analysis to five semantic levels: Data, Information, Knowledge, Wisdom, and Purpose. The DIKWP model can be regarded as an extension of the classic DIKW (pyramid) framework, in which the representation of the "intention" (purpose/motivation) of the system is added on the basis of data-information-knowledge-intelligence, so that the goal-oriented behavior of the algorithm and the system can be quantitatively considered. This hierarchical semantic model can capture the structural elements of cognitive intelligence systems more comprehensively: the data layer focuses on objective perception, the information layer focuses on symbolic representation and pattern recognition, the knowledge layer embodies rules and associations, the intelligence layer involves decision-making and strategy, and the intention layer represents goal-driven and value judgments. Compared with the traditional planarized complexity model, DIKWP provides a layered, holistic, and semantic-oriented complexity expression framework. It not only allows the complexity of each layer to be measured separately, but also supports the analysis of the impact of semantic transformations between layers on the overall complexity, thus significantly enhancing the ability to characterize the complexity of AI systems.

It is important to note that the DIKWP model originally originated from the intellectual origins in the fields of knowledge management and cognitive science. As early as 1989, Ackoff et al. proposed the Data-Information-Knowledge-Intelligence (DIKW) hierarchy to describe the cognitive process by which raw data is processed and refined into information, then elevated to knowledge, and finally gives birth to wisdom. The DIKWP model inherits this hierarchical idea, and combined with the development of artificial intelligence, it adds a focus on "intention" to meet the modeling needs of goal-oriented behavior in autonomous agents. Duan Yucong and other scholars further put forward the theory of "Relation Defines All Semantics" (RDXS), which expands the traditional knowledge graph into an interrelated five-layer semantic graph (data graph, information graph, knowledge graph, wisdom graph, and intention graph) with the help of the DIKW conceptual system, which can map incomplete, inconsistent and imprecise subjective/objective cognitive resources in reality. This indicates that the DIKWP model has a unique advantage in expressing the uncertain semantic relationship of complex systems, and can provide strong support for the semantic modeling of artificial consciousness systems. In the interaction scenario of artificial consciousness and advanced cognition, the DIKWP model is helpful to realize the effective mapping of the subjective internal cognition and objective external expression of the interactive subject. By building a problem-oriented and intent-driven technical framework, the DIKWP methodology can alleviate the problem of opaque AI decision-making process and realize the visualization and explainability of human-computer interaction. This is critical for building bidirectional explainable, trustworthy AI systems, highlighting the potential of the DIKWP model to meet AI ethics and governance requirements.

In summary, this article will be a comprehensive extension of the existing simplified content. Focusing on the core case of artificial consciousness and cognitive intelligence system, we will systematically discuss the complexity analysis methodology of the DIKWP model, including: (1) demonstrating the advantages of the DIKWP model in the modeling of cognitive intelligence system and its enhancement effect on complexity expression; (2) Explain in detail the definition and connotation of each layer of DIKWP (data D, information I, knowledge K, wisdom W, and intention P), derive the complexity calculation formula, and give the theoretical basis and typical metric indicators; (3) analyze the complexity introduced by the interaction between layers, and establish a mathematical model to characterize the evolution of the overall complexity; (4) Introduce at least three instance scenarios (such as AI education system, autonomous unmanned system, and multi-modal large model platform) to analyze their complexity performance characteristics and optimal control paths in each layer of DIKWP; (5) Introduce cutting-edge concepts such as semantic elasticity, relative complexity of subjects, and semantic space circulation, and construct corresponding quantitative analysis frameworks to incorporate them into the complexity evaluation system; (6) Discuss the integration of DIKWP method with current mainstream AI frameworks (including Transformer large model, reinforcement learning paradigm, multi-agent system, etc.); (7) Combining the perspectives of cognitive science, complex systems theory, computational neuroscience and other fields, the multidisciplinary connection of DIKWP complexity analysis is established. Through the expansion of the above contents, this paper hopes to form a complexity analysis system with rigorous structure, sufficient citations and cutting-edge academic value, which will provide a scientific reference for the theoretical research and engineering practice of artificial consciousness and cognitive intelligence systems.

Overview of the DIKWP model and modeling advantages

The DIKWP model divides the intelligent system into five layers of data, information, knowledge, intelligence, and intention according to the semantic abstraction level, and each layer performs its own function and is interconnected with each other, forming a semantic network of gradual abstraction. The data layer (D) corresponds to the objective data of the original sensory input or recording; The information layer (I) is the representation of data after it is structured and given semantics; The knowledge layer (K) contains rules, concepts and their associations, which constitute the knowledge base of the system; The intelligence layer (W) involves the ability to make global planning, dynamic decision-making, and strategy selection based on knowledge; The intent layer (P) represents the purpose, intent, and value orientation of the system. In this model, the lower layer provides the foundation and support for the upper layer, and the upper layer constrains and guides the lower layer, and the five layers together form a complete cognitive computing framework. Through the hierarchical characterization of DIKWP, we can adopt different complexity measures for different levels, so as to obtain a panoramic understanding of the complexity of the system.

It is worth emphasizing that the DIKWP model has significant modeling advantages and complexity expression capabilities. First, the hierarchical structure allows complex systems to be disassembled into smaller subsystem blocks, and there are far more high-frequency interactions within each layer than between layers, forming a "nearly decoupled" architecture. This is similar to what Herbert Simon describes as a "near-decomposable" system structure – subsystems are tightly coupled internally and communicate only externally through a limited number of interfaces, a hierarchical architecture that greatly reduces the overall complexity of the analysis. Specifically, under the DIKWP framework, we can measure the complexity of different stages such as perception, cognition, decision-making, and intention, avoiding the embarrassing situation that the traditional single indicator is difficult to take into account the multi-layer confounding phenomenon. For example, for highly complex agents such as artificial consciousness systems, the DIKWP model provides a complete semantic chain from sensory input to goal planning, enabling researchers to quantify system behavior from multiple perspectives such as data statistics, information entropy, knowledge relevance, decision-making complexity, and intention diversity. At the same time, the explicit division of semantics at each level helps to locate the source of complexity: we can clearly distinguish whether the explosion of perceptual data is causing the increase in complexity, or the exponential increase in the combination of decision-making solutions is causing the complexity bottleneck, and take targeted optimization measures accordingly.

Furthermore, the DIKWP model shows a strong ability to deal with uncertainty semantics. Traditional knowledge graphs mainly cover explicit entity relationships, but the introduction of the intent layer allows subjective factors to be included in the modeling category. The RDXS semantic model proposed by Duan et al. shows that the knowledge graph can be extended into a five-fold graph system including data, information, knowledge, wisdom, and intention with the help of DIKWP structure, which is used to map multi-sourced, incomplete and inconsistent subjective and objective resources in the real world. This mapping method enables the system to represent and fuse noisy, fuzzy, and conflicting information at the semantic level, thereby resolving uncertainty. For example, if there are inconsistencies between data from different sources, the information layer can find out the conflict points through topological association, the knowledge layer can standardize and correct according to logical rules, and the intelligence layer can adjust the decision-making strategy accordingly, and finally evaluate which scheme is more in line with the purpose and value orientation of the system at the intention layer. This bottom-up purification and top-down constraining process enables the system to maintain semantic consistency and decision-making reliability in a complex and changing environment. This is especially true in the context of artificial consciousness: the DIKWP model provides a platform for two-way mapping between subjective consciousness content (such as goals and preferences) and objective environmental information, and the machine can disassemble the vague high-level intentions of humans into executable low-level operations, and at the same time, it can also generalize and promote the low-level massive data into high-level knowledge that is meaningful to humans. This two-way explainability is an important feature of the next generation of human-machine integrated intelligent systems.

Figure 1: Schematic diagram of the mapping of subjective and objective resources of multi-source imprecision, incomplete, and inconsistent human-machine-object interaction to the semantic graph of each layer of DIKWP. The diagram shows how to transform the chaotic and diverse raw resources into structured data graphs, information graphs, knowledge graphs, wisdom graphs and intention graphs through the processes of data clustering, information topology association, knowledge logic specification, wisdom value quantification and intent functionalization. In this process, a large number of low-level details are abstracted by high-level concepts, and semantic information is gradually propagated and fused between levels: the clustering of the data layer compresses the scale of massive raw data, the topological association of the information layer transforms the data pattern into a relational network, the logical specification of the knowledge layer further generalizes the information into inferential knowledge rules, the intelligence layer evaluates the value of knowledge to select the best strategy, and the intention layer finally puts the strategy into functional goal execution. Through the above graphical representation, cross-level semantic flow and uncertainty processing are realized, and the complexity of the whole system can be effectively represented at different abstraction levels.

In summary, the DIKWP model lays a new foundation for analyzing the complexity of intelligent systems through clear hierarchical division and semantic integration. The following is an in-depth analysis of each layer, and the definition, formula derivation, theoretical source, and practical indicators of the complexity of each layer are given to build a comprehensive complexity measurement system.

DIKWP Layer Complexity Measurement

Layer D: Data complexity

Definition: The data layer corresponds to the original set of data perceived by the system, including sensor readings, raw input signals, log records, and other lowest-level information carriers. The complexity of this layer reflects the amount of raw data and the size of the data dimensions that the system needs to process per unit of time. Intuitively, the complexity of the data layer depends on the size of the data and the sampling rate: the larger the number of data points and the faster the generation rate, the higher the complexity of the data layer processing. For example, in a visual perception system, the large number of pixels per second generated by a high-definition camera creates a direct complexity challenge for subsequent processing.

Typical metrics: The total number of data points, data dimensions (such as the feature length of each data point), sensor sampling frequency, etc., are all direct indicators of data complexity. Estimating the size of the raw input to a data layer in terms of (number of data points) is a common and valid method. If the system needs to process raw data points per second, the data layer complexity can be considered to be proportional to N in magnitude.

Complexity Formula: In common cases, data layer complexity can be expressed as:

,

That is, linearly proportional to the number of data points. This means that if the amount of data that the system needs to process doubles, the computational resources (such as time) consumed by the data layer will roughly double. For example, if the camera sensor of an unmanned vehicle collects 640×480 resolution video images at a rate of 30 frames per second, the number of pixel data points generated per second is about . As a result, the original input complexity of the data stream is about 10 million data points per second. Such a large N poses a severe test for real-time systems, which need to be efficiently optimized in hardware and algorithms.

Theoretical Sources and Analysis: The complexity of the data layer basically follows the measurement method of input size in classical computational complexity theory. In algorithmic analysis, the time complexity is usually expressed as a function of the input scale n; Corresponding to the data layer of the intelligent system, n can be analogous to the number of data points N. For example, if you do a Fast Fourier Transform (FFT) for a time series signal with a length of M, the complexity of the algorithm is, but from the perspective of the data layer, we can also consider that the number of data samples to be processed is M, so the data size M is still the dominant factor in complexity. In other words, the data layer complexity metric emphasizes the growth trend in quantity, and has less to do with the specific type of operation performed, and more concerned with how much data needs to be "touched". For example, if a dataset of N pixels is processed pixel-by-pixel, the lower bound of time complexity will increase linearly with N without further optimization, i.e., regardless of the operation performed on the image (filtering, compression, or simple traversal), i.e. This is a striking feature of data layer complexity: it is directly controlled by the size of the data.

However, in a real-world system, data layer complexity can also be affected by data dimensions and structure. For example, high-dimensional data (e.g., hundreds or thousands of features per point) may require more operations to process, resulting in an actual complexity of (where d is a dimension). In addition, the way the data is organized (e.g., whether it is stored in continuous memory, whether it is sorted) can also affect the constant factor or even the order. Overall, however, the cornerstone of the complexity analysis of the data layer is still an order of N inputs. In the DIKWP methodology, we focus on the data layer mainly to obtain a lower bound estimate and starting point of the complexity of the entire system: if even the original data is too large to read, there is no way to talk about the subsequent layer. Therefore, in many optimizations, reducing the complexity of the data layer is the primary strategy, such as reducing redundant data collection, using lower data resolution, and pre-filtering of data, so as to make N as small as possible and control the complexity scale from the source.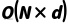

Layer I: information complexity

Definition: An information layer represents a meaningful representation of patterns, features, or symbols extracted from raw data. "Information" here refers to the intermediate results that have been processed and interpreted, such as the feature vector formed by feature extraction of the sensor signal, the information unit obtained by word segmentation and grammatical analysis of the original text, and the target list obtained by image recognition. The complexity of the information layer reflects the computational complexity and multi-source fusion difficulty required in the process of transforming data into information. The main factors affecting the complexity of information include the cost of the feature extraction algorithm (linear, log-linear or higher complexity), the depth of multi-channel information fusion (whether it is necessary to combine information across modalities or sources), and the complexity of event composition (the combination of multiple independent events or signals needs to be considered at the same time). The information layer actually acts as a transition zone from "data to knowledge", and its performance in complexity inherits both the impact of data size and the complexity of the algorithm itself.

Typical metrics: The number of basic operations or features that need to be performed to extract information from N data points is represented by symbols, and the complexity of the information layer can be regarded as an increasing trend. Common metrics include: feature number (the number of meaningful features extracted), pattern type (pattern type/event type recognized), number of fusion channels (number of data sources participating in information fusion), etc. For example, in computer vision, if edge detection is performed on an image of a pixel, the typical number of operations is proportional to the number of pixels, ie. Another example is to perform spectral transformation (such as FFT) on a voice signal of length M, and the operation complexity is about . These indicators reflect the complexity function of the information processing algorithm with respect to the data scale N.

Complexity Formula: Information layer complexity can generally be expressed as:

,

where is some kind of function that does not exceed the polynomial growth. Ideally, feature extraction or information transformation algorithms should not be more complex than linear or linear logarithms (otherwise it would be difficult to be real-time in the face of big data). In many cases, close to or. For example, the complexity of the image edge detection algorithm described above is (equivalent to a constant number of operations per pixel); The complexity of the fast Fourier transform of a speech signal is . More generally, if we extract F features from N pieces of data, the usual form can describe the growth of the number of features with the amount of data, where α≤1 corresponds to linear or sublinear extraction, and α>1 means that more and more information features are derived per unit of data (this is less common in fine analysis, but can occur in the case of multiple combinations of features).

It should be noted that it also depends on the need for information fusion. When the system needs to fuse the content of multiple data sources into comprehensive information, the complexity may increase as a product rather than simply additive. For example, in multimodal information fusion, suppose there are two sensor data streams, each producing N1 and N2 pieces of data, and if you need to match each piece of data to each other, the worst-case complexity is required. However, it is usually possible to reduce the computational effort of fusion through feature filtering and association matching algorithms. For example, only the window matches in time, or the high-level features are extracted separately and then matched, so as to avoid exhaustive combinations.

Theoretical Sources and Analysis: The complexity of the information layer is affected by both the information theory and the complexity theory of pattern recognition algorithms. On the one hand, according to Shannon's information theory, the entropy of the information contained in each piece of data determines the upper limit of extracting useful information. If the data is very redundant or noisy, the computational effort required to extract meaningful information can be more complex because the signal needs to be separated from the noise. On the other hand, from the perspective of algorithms, various feature extraction and pattern recognition algorithms have their own complexities: for example, the computational complexity of convolutional neural network (CNN) to extract image features is related to the size of the convolutional kernel, the depth of the network and the size of the image; The decision tree summarizes the information pattern from the data, and its construction complexity is related to the product of the data dimension and the number of samples. The complexity of information extraction mined by association rules can grow exponentially (in the worst case) with the size of the data. The complexity of these algorithms is directly reflected in the information layer. Therefore, the analysis of the complexity of the information layer needs to be combined with the specific information processing method and the form of evaluation.

In practice, a rule of thumb is that moderate information preprocessing can be achieved at a small cost in exchange for a significant reduction in complexity in subsequent layers. In other words, the time spent or time behind the data layer to extract refined information features tends to reduce the burden of exponential search or highly complex reasoning at the knowledge and intelligence layers. Therefore, the information layer is often regarded as a "complexity control valve": we want to optimize the feature extraction algorithm to keep the C_I as low as possible, but we need to ensure that the extracted information is comprehensive enough to support subsequent decisions. Typical optimization measures include the use of fast signal processing algorithms (e.g., FFT, fast filtering), dimensionality reduction techniques (e.g., PCA to reduce the number of features), feature selection (elimination of redundant or related features), and hierarchical fusion strategies in multi-sensor information fusion (step-by-step fusion rather than fusion of all sources at once). By doing so, it is possible to reduce the growth rate while maintaining the amount of information, thereby optimizing the complexity of the information layer.

Layer K: Knowledge complexity

Definition: The knowledge layer corresponds to the structured knowledge base owned by the system, including symbolic knowledge (e.g., rules, facts), statistical knowledge (e.g., probabilistic model parameters), and modeled experience (e.g., weights learned in machine learning models). The knowledge layer is the link that connects information and wisdom: it inherits the symbols refined by the information layer, and the reasoning and decision-making of the intelligence layer is initiated below. The complexity stems from the cost of storing, retrieval, and reasoning in a vast knowledge space. Typical knowledge-layer tasks include: retrieving relevant entries from the knowledge base, making logical deductions based on knowledge, invoking existing models for inference, and so on. The complexity of these tasks often depends on the size of the knowledge (the number of elements in the knowledge base) and the structure of the knowledge organization (e.g., whether there is an efficient index, whether exhaustive search is required).

Typical indicators: If K pieces of knowledge (such as K facts, rules, or concepts) are stored in the knowledge base, and R-related rules or queries need to be considered when reasoning or matching, the complexity of knowledge layer operations is typically related to K and R. It can be used to represent the number of knowledge items that need to be checked during a retrieval/inference process, and the total size of the knowledge base. Other metrics include the relevance of knowledge (how many other knowledge each piece of knowledge is linked to on average), the branching factor of knowledge query (how many sub-inference branches need to be split into a single inference), etc. These metrics affect the search complexity of the algorithm in the knowledge space. For example, an unoptimized knowledge retrieval requires traversing K record matching conditions, then; If a hash index is used, the average can be reduced to a constant or logarithmic scale; The complexity of the association query based on the knowledge graph is related to the node degree and graph diameter. In logical reasoning, if there are R rules that need to try to match K facts, the worst-case combinatorial complexity is. Therefore, sum is a basic quantitative indicator to capture the complexity of the knowledge layer.

Complexity Formula: For the knowledge layer, the following complexity expression can be given:

,

where K is the storage scale of the knowledge base, and R is the number of knowledge items involved in retrieval or inference. In the most naïve case, it may be necessary to match the R rule to the K knowledge one by one, so the complexity is productive. However, most knowledge operations can be significantly optimized by introducing appropriate data structures and algorithms. For example, using a hash table or a balanced tree to store knowledge can reduce the complexity of a single retrieval to or, making it close. Another example is pattern matching based on inverted indexing, which can avoid traversing the entire knowledge base and only need to directly locate candidates for phase keys, thus greatly reducing the actual size. Therefore, the above equation gives more like the upper bound complexity of knowledge operations; In the actual system, structured storage and pruning strategies are usually between sublinear and linear.

In order to illustrate the source of knowledge complexity, consider two extreme cases: one is a flat and unordered knowledge base without any indexing aid, then retrieving a certain knowledge requires an average of K records, and in this case, if the R rule is to be applied to the reasoning, an R×K match check must be performed, which is the worst-case scenario. The second is a highly indexed and well-organized knowledge base, for example, if the hash or B-tree index Facts is used, then the average of the relevant knowledge is or , then the complexity of the process of applying the R rule is about, which is almost independent of the total size of the knowledge base. These two cases define the upper and lower bounds of the complexity of the knowledge layer. The reality lies somewhere in between: knowledge is often partially organized through hierarchical categories, map links, etc., but still requires a certain range of searches. In addition, combinatorial explosion problems can arise in knowledge reasoning, where the combination of certain rules with each other may produce exponentially new knowledge, especially in logical derivation (e.g., theorem proof, constraint solving). In fact, in computational complexity theory, generalized logical reasoning is proven to be NP-complete, and many inferences involving knowledge inevitably face exponential complexity in the worst-case scenario. For example, the reasoning problem of first-order predicate logic is semi-decidable (there is no universally valid polynomial algorithm); The propositional logic satisfiability problem (SAT, formally a form of intellectual reasoning) is NP-complete. These complexity results remind us that once the knowledge layer is involved in complex combinatorial reasoning, it can be much more complex than simple models. However, in DIKWP complexity analysis, we focus on common operations and averaging cases, limiting the complexity to the polynomial range to make the analysis meaningful.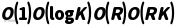

Theoretical Source and Analysis: Knowledge layer complexity is closely related to database retrieval theory and logical reasoning complexity theory. In terms of database retrieval, various index structures (such as B-trees, hash indexes) and query optimization techniques are designed to reduce the complexity of data retrieval. In the field of knowledge representation, graph structures (such as semantic webs and knowledge graphs) provide a way to narrow the search scope by using local adjacencies, so that the query complexity depends more on the local degree of the graph than on the global scale. This can be seen as keeping it within a relatively small range, thus avoiding the occurrence of direct rides. At the same time, in the research of expert systems and reasoning machines in artificial intelligence, people use methods such as forward chain reasoning, reverse chain backtracking, and heuristic search, which are also to deal with the complexity of knowledge reasoning. For example, the well-known heuristic algorithm can reduce the search complexity from exponential to close to polynomial, which is equivalent to using knowledge (heuristic functions) to guide the decision-making of the intelligence layer, thereby reducing the number of branches to be considered in the knowledge layer in advance.

When actually building intelligent systems, we often reduce complexity through knowledge compression and reduction: this includes removing irrelevant or redundant knowledge, merging duplicate rules, or hierarchically organizing knowledge to reduce the domain covered by each inference. For example, in the medical diagnosis expert system, the medical knowledge base is divided by specialty, and if the problem belongs to the category of heart disease, there is no need to load the knowledge of dermatology, so as to effectively narrow it down. Or use knowledge distillation technology to condense large knowledge models into smaller models to reduce the cost of inference. These measures are essentially to reduce the search space of the knowledge layer and ensure that it remains in a controllable range.

In conclusion, the complexity of the knowledge layer reflects the difficulty of efficient search and reasoning in a large knowledge space. Through rational data structures, algorithms, and knowledge organization, we strive to make the complexity of the knowledge layer increase approximately linearly with the size of the task, and avoid exponential loss of control due to combinatorial explosion. The introduction of the DIKWP model enables us to clearly focus on the position of the knowledge layer in the overall system complexity and apply the corresponding optimization strategies.

Layer W: Intelligence complexity

Definition: The intelligence layer represents a system's ability to leverage knowledge for global planning, dynamic policy development, and complex decision-making. This layer involves putting knowledge into practice and choosing the best course of action in a changing environment. The complexity of the intelligence layer is mainly due to the size and structure of the decision-making space: the number of possible states, the number of actions to choose from in each state, and the depth of steps that need to be considered to achieve the goal. To put it simply, the intelligence layer needs to search for a solution (or approximate solution) that satisfies the target in a huge solution space, and its complexity is closely related to the size of the state space and the efficiency of the search/planning algorithm. In addition, the existence of multi-objective decision-making (which requires trade-offs between multiple objectives) or dynamic policy adjustments (where environmental changes prompt policies to be updated in real time) can significantly increase the complexity of the intelligence layer.

Typical metrics: A is about or (without pruning) if the possible state space size of the system (number of states), A is the average branching factor of the state, and D is the depth of steps involved in the decision scheme. Commonly used metrics to measure the complexity of the intelligence layer include the size of the state space, the branching factor (the number of possible actions per state), the depth of planning or the length of the decision chain, and the number of policy generation. where S is an overarching indicator that reflects the scale of the problem itself; Rather, it represents the number of different policy scenarios that are generated and evaluated in a multi-policy scenario. For example, in a path planning problem, the state space can be the total number of possible location nodes on the map, the number of directions that each location may move, and the length of the path steps. For example, in a chess game, S is equivalent to the total number of possible games, the number of choices that can be made for each move, and the level of the number of moves that are expected to be searched.

Complexity Formula: For the intelligence layer, complexity can be approximated as 

,

If it is assumed that the planning/decision-making algorithm can make efficient use of knowledge constraints, the decision is limited to the relevant state subspace. But in general, you need to consider situations where you might build and evaluate a policy multiple times, which can be scaled to

,

where G is the number of times the policy was generated or evaluated. For example, if the system needs to compare different planning scenarios, each of which involves traversing a state space on an S-scale, the total complexity is multiplied by a factor. A concrete example: in a path planning problem with a map size of 1000×1000, the state space is maximum. The heuristic A algorithm is used to find the complexity of a single path of the same order, that is, the magnitude. If you need to try to make trade-offs between multiple strategies such as obstacle avoidance, shortest circuit, and energy optimization (assuming a combination of different weights), you may perform multiple plans, and the total complexity will be approximately increased.

Of course, in decision planning, the actual complexity is strongly related to the efficiency of the algorithm. Heuristic algorithms, pruning strategies, hierarchical planning, etc., can greatly reduce the number of nodes actually searched, so that the number of effectively explored states is much smaller than that of theoretical S. Ideally, a well-performing intelligent layer algorithm will control the number of states that need to be evaluated to be linearly related to the size of the problem, so it can be seen as such. However, in the worst-case scenario or in the absence of good heuristics, the search may have to traverse most or even all combinations of states, exponentially exploding in complexity (e.g., decision tree complexity at exhaustive depth D). Therefore, the above formula can be understood as two estimates, ideal and general: assuming adequate pruning and heuristics, and taking into account possible multi-strategy attempts.

Theoretical Sources and Analysis: The theoretical basis of the complexity of the intelligent layer is derived from the artificial intelligence search algorithm and combinatorial optimization theory. In AI, the complexity of planning and decision-making problems has been studied for a long time: classic results such as the Traveling Salesman Problem (TSP) are NP-difficult, the complexity of chess games is beyond the scope of feasible searches, and so on. These suggest that the complexity of the intelligence layer may be exponential for general complex decision-making tasks. However, by introducing domain knowledge (from the knowledge layer) and heuristics, we can often limit the actual search to a smaller subset of the exponential space. A typical example of this is the algorithm: using heuristic functions, the number of nodes that need to be scaled is drastically reduced to the number of states that the true optimal path passes, without having to traverse the entire graph. Under good heuristics, the time complexity is close to linear to the state number S. Another example is Monte Carlo tree search, in which the search work of the giant game tree is limited to the most promising branches through random simulation and evaluation pruning in game decision-making. Similarly, the dynamic programming approach polynomializes the exponential problem by reusing the subproblem solution, which can be seen as using intelligence (algorithmic strategy) to reduce the effective state space. In short, a series of approaches in the field of AI decision-making are all about countering the complexity of intelligence layer problems.

The DIKWP framework highlights the constraining effect of the knowledge layer on the complexity of the intelligence layer: knowledge can constrain the decision search to a certain extent, so that the complexity of the intelligence layer can be controlled. If the knowledge layer provides perfect rules and models, the wisdom layer can directly deduce decisions based on knowledge without blind search, and the complexity is greatly reduced. On the contrary, if there is a lack of knowledge, the intelligence layer has to conduct large-scale searches to fill the knowledge gaps, and the complexity increases dramatically. This is reflected in the trade-offs between the W/K layers: if there is sufficient knowledge, the wisdom search will be simplified, and if there is insufficient knowledge, the wisdom complexity will increase. Therefore, when designing agents, it is common to reduce the state space that the intelligence layer needs to explore by adding knowledge (such as adding a rule base or training an empirical model).

Another source of complexity for the intelligence layer is multi-objective coupling. When a system is faced with multiple goals at the same time (e.g., an autonomous vehicle needs to take the shortest route while avoiding danger and saving energy), the intelligence layer must consider the goal trade-offs when generating policies. This adds another dimension to the decision-making space, requiring switching between different target strategies or evaluating them in parallel. If not handled properly, it can lead to a spike in portfolio complexity. Generally, the multi-objective optimization theory can be introduced to transform the multi-objective problem into a series of single-objective problem solving through weighted sum, hierarchical optimization, etc., so as to avoid exponential complexity. For example, there are two phases of planning: the first phase satisfies hard constraints such as safety, and the second phase optimizes the path length or energy source while satisfying the results of the first phase. In this way, the big problem is disassembled, and the actual complexity is the sum of the complexity of the sub-problems, not the product.

In order to suppress the complexity of the intelligence layer, we have several entry points: one is pruning and heuristics, which use domain knowledge to reduce useless searches; The second is hierarchical decision-making, which distinguishes long-term goal planning from local immediate response, and plans for their own small problems in a hierarchical manner. The third is parallel search, which uses multi-threading or multi-agent to explore different parts of the space at the same time to speed up the search (but this is equivalent to increasing the parallelism of resources rather than reducing the progressive complexity in complexity analysis). In addition, the learning strategy is also one of the trends, that is, using machine learning to train an approximate decision model in the offline stage, which approximates the output of the decision at runtime in constant time, thereby greatly reducing the online complexity. However, the training itself is costly, and there is a trade-off between overall efficiency. In the DIKWP framework, the complexity analysis of the intelligent layer reminds us that decision-making problems are often one of the main bottlenecks of complexity, but it is precisely the introduction of innovative algorithms and structures at this layer that can produce qualitative efficiency improvements.

P-layer: intent complexity

Definition: The intent layer represents the set of goals, task planning, and subjective intentions pursued by the system. It is at the top of the DIKWP architecture and dictates the direction of the system's behavior. In a single-task environment, the intent may be fixed (e.g., navigating to a specified destination); However, in complex multitasking environments or interactive scenarios, intent may change dynamically or be negotiated across multiple subjects. The complexity of this layer comes from the complexity of target switching, task scheduling, and intent coordination. Additional complexity overhead is introduced when a system needs to change its goals during operation, when it is necessary to choose between multiple tasks, or when multiple agents need to coordinate their own intentions. This includes re-planning new goals, computations for allocating resources across different tasks, and dealing with the costs of multi-objective conflicts and consistency.

Typical metrics: T is used to denote the number of intent/task switching during the operation of the system, and L is the number of replanning or feedback adjustment cycles that accompany each switching (i.e., the length of iterative process required to accommodate the new intent). In addition, in a multi-agent or multi-task environment, metrics such as the size of the intent space (the number of possible different target kinds) and the degree of intent coupling (the strength of the goal association between different subjects or tasks) can be defined. Together, these metrics affect the complexity of the intent layer: frequent target switching (large T), complex adjustment process (large L), or multiple goals that are highly correlated and need to be repeatedly coordinated will increase the complexity of the intent layer.

Complexity Formula: The intent layer complexity can be expressed in the following form:

,

where T is the number of intention changes and L is the number of feedback adjustment cycles involved in each adjustment. Intuitively, if the system always runs around a single goal (T≈1, no switching), then the intent layer only introduces complexity once when the goal is initially set, and does not increase the burden later. However, if the system needs to switch frequently between different goals/tasks (e.g., multitasking, interactive dialogue system constantly changes goals according to user needs), each DIKW layer needs to be adjusted accordingly, and the cost is proportional to the switching frequency T. The number of feedback loops required for each intent adjustment, L, reflects the length of the iterative process required to converge on a new goal. If the adjustment process requires multiple rounds of information collection-decision-evaluation feedback loop (e.g., the autonomous system repeats trial and error under a new task to calibrate the strategy), the L is larger and the complexity increases accordingly.

For example, a smart home assistant manages both security and energy optimization goals. When an intrusion event is detected, it needs to temporarily switch intent to prioritize security (T increases by 1); After the event is over, switch back to daily energy optimization (T plus 1). Each time an intent is switched, it needs to re-plan the scheduling of sensors and devices (e.g., mobilizing cameras, pausing air conditioning, etc.), which may involve several feedback loops to stabilize the new state (assuming each time). Then, if T = 2 switches occur over a period of time, the total intent layer complexity may be about (only a rough count is made here). For example, when a multi-agent UAV formation performs a mission, the local intent of each UAV needs to be coordinated with the global mission intent. If the formation or division of tasks is adjusted every once in a while, which is equivalent to a global intent reorganization, then depending on the number of team members and the coordination algorithm, each reorganization may require a certain iteration of communication (L) to reach a consensus intent. Frequent restructurings or large-scale collaborations can drive up the complexity of the intent layer.

Theoretical source and analysis: The intent layer complexity can be understood from two perspectives: task scheduling theory and multi-agent planning. In the context of single-system multitasking, the intent to switch is similar to the process switching of the operating system, and frequent context switching will bring overhead (increased complexity). The scheduling theory shows that in the hard real-time system, frequent task switching increases the complexity and system overhead of the scheduling algorithm, which is consistent with the view that C_P increases with T. Similarly, if the task switch involves recovery and cleanup of the context (equivalent to a feedback loop adjusting the system state), an extra step L is introduced. Therefore, the ** form can also be regarded as the quantification of additional complexity caused by task switching.

In multi-agent collaboration, distributed planning and consensus algorithms study the complexity of multiple agents coordinating common goals. For example, reaching a consensus intention (consensus) for multiple agents often requires iterative information exchange. The complexity of the classical consensus algorithm is related to the network topology and the number of iteration rounds: it usually takes rounds of communication to make all the subjects' intentions agree or converge to a certain error range. Therefore, if a multi-agent system frequently needs to re-agree on different tasks, it will also be amplified. To make matters worse, when there is a conflict of intent between the parties, the negotiation or game process itself may be exponentially complex (e.g., the general multi-party game equilibrium problem). However, in the DIKWP framework, we tend to classify this part of the complexity into the game decision complexity of the intelligence layer, while the intent layer mainly describes the frequency of switching and scheduling.

The role of the intent layer in overall complexity can be understood in this way: it is equivalent to the "top-level control logic" of the system. If the top-level control logic is stable and clear (almost unchanged goal), the system can be optimized in one direction for a long time, and the complexity of each layer tends to be stable. If the top-level logic keeps changing direction (changing targets frequently), then it is tantamount to making the system "keep restarting new problems", and the accumulated complexity is similar to the number of switches. This kind of overlay sometimes even causes additive loss due to interference between the old and new targets, which is manifested as a higher complexity than linear increase (e.g., frequent switching leads to invalid cache, learning forgetting, and needs to be compensated for at an additional cost). Therefore, a common approach in engineering is to reduce unnecessary switching, maintain intent stability, or set up meta-scheduling at a higher level (reducing the actual frequency of switching) to reduce the complexity introduced by the intent layer.

In general, the intent layer complexity emphasizes the cost of the macro-control process of the system. With proper task planning and intent management, the number of goal changes can be minimized, and the transition when changing is fast and smooth (reducing the number of feedback iterations C_P) can be kept to a low level. For example, predictive scheduling allows the system to switch tasks in a planned way instead of randomly, or continuous learning allows the system to partially follow an existing strategy when switching targets (reducing the number of readaptation cycles). These strategies can be thought of as optimizing at the intent layer, which indirectly improves the complexity performance of the entire system.

Interlayer coupling complexity and global evolution model

The complexity analysis of the above layers is relatively independent, but in the actual system, the layers of DIKWP do not operate in isolation, but form an organic whole through interactive coupling. The output of one layer often becomes the input of the previous layer, and there are feedback loops and bidirectional effects between layers. This interlayer coupling may result in a different behavior from the simple addition of layers: it may be higher than the linear superposition of the complexity of each single layer (with synergistic gain or additive loss), or it may be lower than the simple additive (with mutual cancellation or efficiency improvement) due to the mutual constraints between the layers. Therefore, it is necessary to build a model to describe the evolution of the overall complexity of the system and understand how the interlayer coupling changes the magnitude of the complexity.

First, you can try to estimate the overall complexity in terms of macro aggregates. Assuming that the computational costs of each layer can be superimposed during a complete operation of the system, a preliminary upper bound estimate can be obtained by adding the complexity expressions of the above layers:

.

This is equivalent to assuming that the layers are executed sequentially and without significant duplication or mutual exclusion – each layer of complexity contribution comes at an additional cost. As previously derived, . Adding these up directly may result in a fairly high upper bound for complexity. However, this simple addition does not take into account interlayer relationships, such as the work of one layer may reduce the workload of another. A more complex, but more practical, approach is to consider couplings: the interaction of layers I and J creates additional complexity, or reduces complexity with each other. The coupling coefficient can be introduced to represent the complexity effect introduced by the interaction of layers I and J, and the overall complexity can be expressed as:

,

where represents the complexity of the first layer itself (in DIKWP order) and is a function that describes the complexity of the interaction between layers i and j, which may take a simple product, linear, or more complex form. is the weight coefficient, which reflects the strength and type of coupling. If the coupling of layers i and j would introduce additional complexity, then the corresponding λ is positive; Conversely, if the coupling leads to efficiency improvement and reduced complexity, λ can be taken as a negative value.

For example, the knowledge layer (K) and the intelligence layer (W) are often positively coupled: knowledge guides decision-making, and decision-making feeds back new knowledge. In the positive and benign case, the rich knowledge base makes the intelligent layer planning more effective (equivalent to negative value, and the overall complexity is reduced); However, if there is ambiguity or conflict in knowledge, the intelligence layer will have to spend an additional cost to screen (which is a positive value and increases the complexity). Another example is the relationship between the data layer (D) and the information layer (I): high-quality data (high complexity of layer D) can reduce the difficulty of information extraction (the complexity of layer I decreases), which is manifested in the fact that although it increases, it decreases, and the two partially cancel each other. Expressed as a coupling term, i.e., negative, offsets a portion of the value. This offset exists in many systems: more data points N (increase) can reduce uncertainty through statistical averaging, thus simplifying information extraction (reduction). Conversely, if the data redundancy is too high, the information layer has to perform a deredundancy operation, causing the C_I to rise beyond linearity, which can be interpreted as a positive value, making the total complexity higher than the simple addition.

Another manifestation of interlayer coupling is feedback loops: systems tend to form a closed loop between multiple layers, with information flowing back and forth between layers until some equilibrium is reached. For example, in automatic control, the sensor data (D) is processed to obtain state information (I), and the decision-making module (W) calculates the control command according to the target (P) and the knowledge model (K) and acts back to the environment, and then the environmental change affects the new data - forming a closed loop. If the system has to carry out a perception-decision-action cycle H times in a task, then the total complexity can be roughly regarded as the sum of the complexity of each layer at a time, i.e., 

.

The P-layer is not considered here, as the target is usually unchanged within the loop (if the target is also adjusted, it should be counted as the P-layer complexity). This equation shows that if the system needs to continuously perceive decisions (e.g., autonomous unmanned systems cycle multiple times per second), the complexity increases linearly with the number of cycles. However, with feedback conditioning strategies, it is often possible to reduce the number of effective cycles. For example, the introduction of feedforward prediction can skip part of the loop, or the perceived frequency can be reduced by filtering, which will reduce the equivalence. In extreme cases, if the system reaches a steady state and no further adjustment is required, it can be considered to be reduced from a certain value to 0.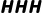

To describe the evolution of complexity more precisely, consider a discrete-time evolution model: let the complexity cost of representing layer i in the tth decision cycle have:

It may be a function driven by an external input, such as a change in the rate of arrival of data;

The complexity of the knowledge layer changes with its own accumulation and the introduction of new information.

The complexity of the intelligence layer is affected by the effectiveness of the current knowledge and the progress of goal completion.

, the complexity of the intent layer is updated based on whether the new target switch is triggered and whether multi-agent coordination is carried out.

Such a model describes the cyclical dependence of complexity: the complexity of each layer affects and co-evolves over time. For example, if there is a drastic change in the external environment at a certain moment, resulting in a large increase in data input (a surge), it will also be pushed up in the short term because more information needs to be processed and more decisions need to be made; However, in the long run, if the system extracts a new model from a large amount of data through knowledge learning (rising), or updating the strategy (reducing the future), the complexity of the subsequent cycle may decrease. It can be said that complexity can be eliminated between different layers: the increase in the complexity of the data and information layer may be exchanged for a decrease in the complexity of the knowledge layer (because the system is smarter and does not need blind search); The reduced complexity of the intelligent layer may mean that more complexity is pushed forward to the knowledge layer for offline processing (such as pre-trained models). This transfer and balance of complexity reflects the core idea of intelligent system optimization: transform real-time complexity into preprocessing complexity, and transform low-level complexity into high-level complexity to achieve optimal overall efficiency.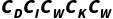

An edge case worth discussing is: does more layers mean more complexity? On the surface, the introduction of more layers will inevitably increase a certain amount of overhead (at least the basic processing of each layer requires resources); On the other hand, more layers provide greater structuring capabilities that reduce the complexity of each layer itself. As Simon points out in The Architecture of Complexity, the hierarchical structure of complex systems is a means of dealing with complexity. Therefore, the DIKWP five-layer architecture does not necessarily increase the total complexity compared with tiling all problems, but may reduce the overall complexity through division of labor and abstraction. The way to measure this is to refer to the concept of effective complexity: it distinguishes between regular parts of a system (compressible patterns) and unordered parts (random complexity). The hierarchical structure of DIKWP helps to separate the ordered part of the problem (the knowledge and wisdom layer deals with structured problems), and the disordered part is limited to the low layer as much as possible (the data noise is handled by the information layer), so as to reduce the effective complexity of the whole world. In other words, despite the complexity of each layer, with a proper architecture, the overall complexity of the system increases more slowly than without architecture, and even reaches some upper threshold.

Mathematically, you can try to define an overall complexity metric. One possibility is to borrow Tononi's concept of Integrated Information and use the Φ value to quantify the complexity and integration of the system as a whole. It depicts the part of the system as a whole that produces more information than the sum of its parts. In the DIKWP framework, if we consider each layer as an information processing module, then the stronger the interlayer coupling and the more integrated the system, the higher its Φ may be. The level of Φ can be understood as the overall complexity of the system (which cannot be explained by the individual parts). This measure is particularly relevant for artificial consciousness systems, as Φ is considered by some theories to be associated with the degree of consciousness. In terms of complexity, the complexity of a high-Φ system is not the sum of the discrete parts, but the parts that have a large number of interactions. This means that the analysis of such systems requires consideration of the contribution of interlayer coupling, i.e., the ** term in the above formula.

Summarizing the above discussion, it is quite complex to accurately describe the overall complexity. However, we can summarize a few rules:

Linear approximation stage: When the system is in the early stage of the task or does not change much, each layer performs its own role, and the complexity approximation can be decomposed into the sum of the layers. In this case, the interlayer coupling plays a small role and can be approximated as 0,.

Coupling enhancement stage: With the development of the task, the interlayer information flow is frequent, and the coupling term rises. For example, when encountering a difficult problem, the wisdom layer frequently calls the knowledge layer (), or the data fluctuation triggers multiple rounds of feedback (, etc. positive values). At this time, the growth is faster than linear, and even there is a non-linear jump.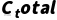 

Stable synergy stage: The system strengthens inter-layer synergy through learning and adaptation, and higher-level patterns emerge, and some couplings become less complex (negative). For example, the improvement of knowledge simplifies the intelligence layer, and the stability of the wisdom strategy reduces the demand for data. Growth slowed or even declined.

New Target Shock Phase: If a new intent or environmental mutation is introduced, a new coupling enhancement process begins, repeating the cycle.

This evolution can be fitted to some extent with piecewise functions or piecewise linear models, i.e., different growth rates for task size (or time) at different stages. For complex systems, we are more concerned with long-term stability: whether there is some mechanism that prevents indefinite deterioration. The biological brain, for example, is obviously an extremely complex system, but the human brain is astonishingly efficient at routine cognitive tasks, far from the level of a combinatorial explosion. This is thought to be due to the brain's hierarchical structure, highly parallel computation, and continuous adaptive optimization (which strengthens valid connections and weakens unwanted ones), which reduces overall complexity.

In line with this line of thinking, in order for AI systems to achieve large-scale cognition and controllable complexity, they must also use the structured approach of DIKWP to divide and solve problems in layers, and reduce unnecessary searches and computations through feedback learning. In the language of complex systems theory, it is to reduce entropy to dimensionality: to reduce the degree of freedom of the system so that it actually behaves on a low-dimensional manifold in a high-dimensional space. The interaction of the various layers of DIKWP is precisely to continuously constrain the effective state of the system, from data to intent, so that the complexity does not expand endlessly. This creates a closed loop of complexity evolution: the system senses complexity, processes complexity, learns to reduce complexity, and repeats itself to maintain efficient operations in a dynamic environment.

Case Study: Application of DIKWP Complexity in a Typical System

In the following, we analyze the complexity performance and optimization strategies of the DIKWP model in the actual cognitive intelligence system through several typical case scenarios. These examples include: AI education systems (intelligent teaching systems), autonomous unmanned systems (such as unmanned vehicles/drones), and multi-modal large model platforms (large AI model platforms with multi-modal interaction). By dissecting the layers of DIKWP in each scenario, we will see the complexity characteristics of different applications and discuss how to take measures to optimize the system complexity at each layer.

Case 1: Analysis of the complexity of the AI education system

Scenario description: An AI education system refers to an intelligent teaching and tutoring system, such as a personalized intelligent tutor for students. The system captures student learning data, provides instructional content and exercises, and dynamically adjusts instructional strategies for each student. We take an intelligent teaching system for mathematics tutoring as an example to investigate its complexity source and DIKWP hierarchical performance.

Layer D (data): The data of the AI education system includes students' practice answer records, classroom interaction logs, physiological sensing data (such as attention monitoring), etc. The complexity of the data layer is reflected in the large amount of student answering information that may need to be processed, especially on an online teaching platform, where thousands of students interact with the system at the same time. For each student, data input includes the time each question was answered, whether it was correct or not, the process of solving the problem (e.g., steps or ideas, which may be in text), and behavioral data such as mouse clicks and time spent on the page. Combined, these data points are quite large. Assuming that each student solves 100 questions a day, and each question records 10 data points (time, true or false, steps, etc.), and 1,000 students generate data points every day, the complexity of the data layer is equivalent to processing millions of data levels per day. If the system is also connected to the camera to capture the students' expression concentration, the video data volume is even larger. However, in general, such systems will preprocess and extract simplified information from the video to avoid the complexity of the data layer. Optimizing the data layer includes aggregating log data in real time (reducing storage frequency), reducing frame rate or resolution for video capture, and reducing the amount of invalid data through event-triggered mechanisms rather than continuous sampling. These can effectively reduce the data layer.

Layer I (Information): The information layer needs to extract meaningful information from the raw student data. For example, the mastery of each knowledge point is calculated according to the answer record, the thinking characteristics of students are extracted from the text of the problem-solving steps, and their learning habits are inferred from the operation behavior. These belong to the process of feature extraction and information fusion. For each student, the system may maintain several features, such as "mastery percentage/memory intensity", etc., which involve aggregating a large amount of problem data and calculating statistics, which are usually linear or linear logarithmic complexity, such as summarizing the accuracy of each knowledge point ( ) or doing a sliding window to count the forgetting curve (possibly). In addition, multimodal data fusion also increases C_I: for example, combining answer records with expression attention data can determine whether a certain type of question is wrong due to carelessness (decreased attention) or lack of knowledge. Multi-source information fusion may require matching timestamps or related events, which introduces a certain degree of combinatorial complexity, but because each fusion is mainly carried out in the same student dimension and the scale is not large (hundreds of data points matching), it can be considered that the C_I still grows nearly linearly with the amount of student data. The key to optimizing layer I is to pick out valid features and avoid "unnecessary information extraction". Common knowledge tracking models in the education system (e.g., Bayesian Knowledge Tracing, Deep Knowledge Tracing) replace a large number of manual feature extractions, which update a few parameters in real time (e.g., mastering probability) through a relatively simple model, shifting the complexity from processing all historical data to updating one model parameter (similar to O(1) operating on each question). Therefore, the introduction of the student knowledge state model greatly reduces the calculation of the information layer: it is no longer necessary to recount the full data every time, but to update it incrementally. In summary, the complexity of the information layer of the AI mentor system is quite low when there is model assistance, and more calculations are transferred to the offline model training stage (which belongs to the knowledge layer or intelligence layer preprocessing).

K layer (knowledge): The knowledge layer of the teaching system consists of two parts: one is the subject knowledge base, which contains the structure of the teaching content (knowledge point relationship, exercise database, etc.); The second is the student knowledge state model or database. For subject knowledge bases, the system needs to retrieve relevant content to recommend the next question or knowledge point to students. For example, when a student makes a mistake about a quadratic equation, the system needs to find out the prerequisite knowledge (such as a primary equation) of the corresponding knowledge point from the knowledge graph to provide review materials. This retrieval complexity depends on the size of the knowledge graph K and the depth of the query. In general, the scale of the subject knowledge graph is not huge (thousands of knowledge points and relationships), and the retrieval usually uses node indexes to quickly locate relevant knowledge points (C_K close to O(\log K) or constants). Therefore, the knowledge base part is less complex. The other part is the student knowledge status, which records each student's mastery of each knowledge point, which is equivalent to a matrix (student × knowledge points) or database query. If you serve M students at the same time, you need to find the student's data in M records for each knowledge point status update retrieval. Per-student storage with a hash table is available at O(1). If the storage is categorized by knowledge points (student mastery in a list of knowledge points), then updating the status of a student's knowledge points requires finding the students in the list (complexity O(\log M) or O(1)). So either way, the complexity of a single update or query is not high. However, the student status database is updated frequently (each question is triggered), and the total complexity accumulation cannot be ignored. If M=1000 students update state 10^5 times per day, the state library needs to undertake 10^5 small-scale write operations. Fortunately, the database management system can handle this concurrency efficiently, making it scale well. In general, the main challenge of the K layer of the AI teaching system is not the retrieval complexity, but the knowledge evolution: for example, dynamically updating the parameters of the student model (learning rate, forgetting curve), or modifying the knowledge structure according to the student data (if two knowledge points are found to be strongly related, they may automatically add new connections in the knowledge graph). The latter involves the learning of knowledge structures, which belongs to the intersection of the wisdom layer/knowledge layer, and its complexity is difficult to quantify, but this update is usually carried out offline and does not affect the online complexity. With pre-orchestrated courses and a well-built knowledge graph, the amount of computation at the K-layer at runtime is minimized.

Layer W (Wisdom): The wisdom layer is embodied in the teaching system for teaching strategy planning and personalized decision-making. For example, the system needs to decide what to present next, whether to explain, give examples, or let students practice. If you practice, which question to choose; When students are not performing well for a long time, whether to adjust the overall learning strategy, etc. These decisions are multi-objective in nature (both to be efficient and to keep students interested) and involve a certain depth of planning (planning the next few learning steps to achieve an overall goal, such as passing an exam). The decision-making space is very large: assuming that the system has 10 different teaching methods, each corresponding to a variety of content choices, then each step of the decision can be seen as a sequence of picking from many options. The wisdom layer is often solved by rules or algorithms: for example, simple If-else rules (if the mastery is low, the basic questions will be explained first), and the complexity of this hard-coded strategy can be ignored (constant time decision); Or use the teaching strategy model trained by reinforcement learning, which directly outputs actions according to the current state during interaction, and each step of the decision is also calculated as O(1). However, in order to obtain these fast decision models, complex planning algorithms or training algorithms may be used behind them. Taking reinforcement learning teaching as an example, offline training needs to simulate thousands of students interacting with the strategy to iteratively update the strategy, and search the huge policy space to find the optimum, which belongs to the preprocessing complexity of the intelligence layer. When running online, this complexity is implicit in the model and is greatly reduced when it is actually executed. Therefore, the complexity of the intelligence layer of the teaching system shows two stages: the offline policy design stage may be an NP difficult problem (for example, the optimization of the teaching process can be regarded as a class of combinatorial optimization), but the complexity of the online execution stage is constrained at a very low level through models or rules. If a system doesn't have a pre-trained strategy and instead executes planning in real time, the complexity increases. For example, some adaptive learning systems run algorithms in real time in the background (such as calculating the learning path of the day based on student performance), and if the algorithm needs to search for many combinations (for example, selecting 10 questions and selecting the best combination from 1000 questions in the question bank, which is equivalent to a large number of combinations), even if a heuristic greedy algorithm is used, it may also have to evaluate the effect of many alternative questions, and the complexity should not be underestimated. Optimization methods include: limiting the set of optional content (e.g., selecting topics from adjacent content of knowledge points instead of the whole database), applying heuristic rules to filter options first, and making phased decisions (first determining knowledge points and then specific topics). These measures can reduce the decision-making space S or effectively reduce the number of alternative strategies G. Therefore, in practice, a mature AI mentor system usually simplifies intelligence-layer decision-making to a limited selection of a few strategy templates, so as to avoid completely groundbreaking planning teaching. In summary, at the intelligence layer, complexity depends critically on the degree of pruning of the decision space: if the pruning is sufficient, it C_W close to constant or linear, and if it is not sufficient, it may explode. However, with years of teaching experience and AI algorithms, this problem can be well avoided.

P-layer (intent): In the AI education scenario, the top-level intent is generally clear and stable—to help students master knowledge and pass exams. This is a human-given goal at the beginning of the design of the system, and it does not change frequently. Comparatively speaking, the intent layer complexity is mainly reflected in multi-student management and teacher/parent requirements. For example, an AI education system serves many students at the same time, and each student's learning goals and progress are different, so the system needs to make trade-offs in resource allocation (such as server computing power tilt and content recommendation priority). If the system needs to constantly adjust the schedule based on each student's priorities (e.g., students approaching exams prioritize more intensive services), then it can be seen as a task scheduling problem on a global scale. But usually this kind of scheduling is more at the engineering implementation level and does not affect the teaching strategy itself. Therefore, it can be considered that the overall intent of the system is unified (to improve the learning effect), but the external constraints (time, resources) may bring some scheduling intentions. Another aspect is multi-agent collaboration: AI tutors may work in tandem with human teachers, which requires strategic consideration of the teacher's plan (e.g., what knowledge points the teacher asks to cover today, then the AI mentor's intentions need to be temporarily subordinated to the teacher's arrangement). This kind of collaboration can be abstracted as the intent fusion problem of different subjects, but in practice, it is usually determined by preset rules and is not very complex. In summary, the intent layer of the education system is relatively simple, with a low T (number of target switches) that only changes when external requirements change or curriculum objectives are adjusted; L (Adjustment Feedback Loop) may manifest as adjusting a class schedule or study plan once and then executing it. As a result C_P does not contribute much to the overall complexity. However, in the future, if we imagine an AI education system that can independently plan long-term learning paths and dynamically adjust the syllabus, then the intent layer will be more active. For example, the system may find that a student is interested in programming and temporarily add a long-term goal to cultivate that direction, which is equivalent to introducing a new goal at the intention level, which needs to be coordinated with the original subject learning goal for long-term planning. In this case, the C_P will increase, but this kind of autogenization is still at the forefront of exploration.

Summary of optimization paths: For the AI education system, each layer has its own focus on optimization: the data layer reduces the amount of data through downsampling and event triggering; The information layer reduces the burden of duplicate statistics and fusion through the knowledge tracking model. The knowledge layer simplifies retrieval reasoning through the fine construction of knowledge graphs and efficient indexing. The intelligent layer avoids online search space through pre-training strategies and heuristic pruning. The intent layer is mainly to reduce external interference due to the clear target. Overall, the complexity management of the education system is relatively successful, which is why in reality the intelligent teaching system has been able to run relatively smoothly. The key is that there is a clear structure (course-knowledge-topic) in the field of education, and the DIKWP model has a high degree of fit and is easy to optimize in layers.

Case 2: Complexity analysis of autonomous unmanned systems

Scenario description: Autonomous unmanned systems include autonomous vehicles (driverless cars), autonomous drones, autonomous delivery robots, etc. This type of system needs to autonomously sense, navigate, and perform tasks in a physical environment, and has high real-time and safety requirements. We take a driverless car as an example for analysis, and its complexity sources and DIKWP stratification are as follows:

Layer D (data): Unmanned vehicles are equipped with a variety of sensors, such as cameras, LiDAR, radar, ultrasonic, etc., which generate massive amounts of data per second. Taking cameras as an example, an unmanned vehicle may be equipped with multiple high-definition cameras (e.g., 8 cameras, each 30 frames per second, resolution 1280×720), and the camera data alone can reach the level of tens of megapixels per second. Lidar emits millions of point clouds per second. Overall, the amount of raw data N per second of a bicycle may be measured in the order of 107-108. Data Layer Complexity C_D = O(N) is at an extremely high level. In order to process it on hardware, the system usually preprocesses or filters the sensor data, such as camera video compression, point cloud downsampling, etc. These pre-processing also consume computational resources, but they are necessary compared to the value of subsequent decisions. The main measures to optimize the data layer include: multi-sensor synchronization and clipping (initiating high-frequency acquisition only when needed, limiting areas of interest such as the road ahead), edge filtering (simple filtering at the sensor node, compression before transmission), etc. The latest unmanned vehicle systems also tend to use new sensors such as event cameras, which do not output fixed frames, but only output data when changing, thereby significantly reducing N. However, in general, the data layer complexity of unmanned systems is still the highest among all layers, because it is better to obtain more information than to miss key clues under safety requirements.

Layer I (Information): The information layer is responsible for converting the raw sensor data into an environmental model and status information. For example, the camera image recognizes the position (feature) of pedestrians, vehicles, and traffic signs through object detection; LiDAR point clouds obtain the distance and shape information of obstacles through clustering. GPS/IMU data fusion obtains the vehicle's own precise position and attitude. These are the results of processing at the information layer. The computing tasks of the information layer can be divided into two parts: perception and fusion: perception includes running various computer vision and signal processing algorithms, such as CNN models for object detection, point cloud segmentation algorithms to find ground and obstacles. Fusion combines information from different sensors, such as using Kalman filtering to fuse IMU and GPS, or using multi-sensor data fusion to estimate the dynamic state of vehicles and obstacles. In terms of complexity, the complexity of a single perception algorithm is approximately linear to the amount of input data (for example, the complexity of the object detection algorithm O(W×H) on an image is related to the number of pixels), but the constant factor is huge because CNN requires a large number of convolution operations. In the same way, the complexity of the point cloud processing algorithm is about O(P log P) or O(P) (P is the number of points), but P is huge. At the same time, the unmanned vehicle perception module may run more than a dozen different models/algorithms in parallel to process different sensors, which is C_I not to be underestimated. Often, C_I is out of C_D because extracting information is more computationally expensive than reading data. For example, reading a frame of an image may take 100 million operations (at the pixel level), while running a deep network to process this image may result in more than 1 billion operations. Therefore, in unmanned systems, information layer complexity is one of the main real-time bottlenecks. This is why there must be a dedicated AI acceleration chip (GPU/TPU, etc.) to support the car. In the fusion phase, the complexity is relatively low because the fusion is based on perceived results (the number is much smaller than the original data). For example, when tracking 10 vehicle targets, the Kalman filter updates the O(1) calculation per target, which is very lightweight. Multi-sensor fusion requires matching targets from different sources, and if it is simply based on spatial proximity matching, O(n) (n is the number of targets). It is only when there are a large number of sensors or complex matching criteria that the complexity of fusion can skyrocket. Unmanned vehicles generally only have a few main sensors, and the fusion algorithm design is also relatively optimized, so the C_I is mainly dominated by the perception algorithm. The key to optimizing Layer I is model efficiency: it includes network compression, pruning, multi-task learning (using one model to complete multiple perception tasks), and rational allocation of computing resources (simplifying some algorithms according to the scenario, such as not detecting pedestrians on highways). With these measures, you can reduce the actual perceived latency and computational load. Future trends such as edge AI chips and local preprocessing will continue to reduce the complexity of extracting unit data.

Layer K (knowledge): The knowledge layer of unmanned vehicles includes static knowledge (such as high-definition maps, traffic rules, and vehicle dynamics models) and dynamic knowledge (such as recently learned new driving strategy parameters, behavior patterns of other road users, etc.). Static knowledge bases, such as high-definition maps, can be large (gigabytes of data in a city map), but they usually only keep a local area of interest (a radius of a few kilometers) on the car and read them on demand using efficient indexes. Therefore, the complexity of knowledge retrieval is low, for example, the vehicle-mounted map engine retrieves the road topology 100 meters ahead according to the current position, and the time complexity O(log K) (K is the number of nodes in the map road network). Traffic rules, for the like, can be hard-coded into a set of rules, and when it is necessary to assess whether a route or action is legal, several related rules (very small R and K) are applied. Therefore, the use of static knowledge has little effect on real-time complexity (it can be thought of as constant time, as long as it is preloaded in memory). In terms of dynamic knowledge, unmanned vehicles will have models to predict the future movement of surrounding vehicles/pedestrians, which is a learned model (such as a motion model based on historical trajectories). Invoking this model inference is also usually at the constant millisecond level and doesn't become a bottleneck. The K layer of the unmanned vehicle also has the vehicle's own dynamic model for path planning constraints, etc., and these equations are simple to calculate. In summary, the vast majority of the knowledge layer of unmanned vehicles is prepared in advance, and the runtime is only a query or simple operation, and its complexity contribution is small. The real challenge is knowledge updating: for example, in a simulation or training environment, the system may be constantly updating the strategy (the intelligence layer part) through reinforcement learning, or fetching a new map/model from the cloud via networking. These belong to the complexity of system learning and maintenance, which do not occur in the real-time closed loop and can be processed offline. For safety reasons, in-vehicle system knowledge is usually frozen or slowly updated, and the internal knowledge structure is not drastically modified while driving, so as not to introduce uncertainty. Therefore, it can be said that the K-layer complexity of unmanned vehicles is highly controlled during operation. It should be noted that the boundaries between knowledge and wisdom are sometimes blurred, for example, path planning algorithms use maps and traffic rules, which are essentially knowledge, but applying them for constraint optimization are intelligence layer examples. Therefore, we have a specific discussion in the wisdom layer, and the knowledge layer part can be summarized as the information that is useful for decision-making has been sorted out in advance, and it is easy to use, efficient and reliable.

W layer (intelligence): The intelligence layer is the core decision-making module of the unmanned driving system, involving sub-modules such as path planning, behavior decision-making, and motion control. Path planning is the search for a global route from the current location to the destination based on a known map and real-time environmental obstacles. This is usually searched on the road network diagram using the A or Dijkstra algorithm, and the number of nodes can reach millions at the city level. Fortunately, the road network structure is sparse and there is heuristic guidance, and the results of algorithm A can be obtained in milliseconds, and the complexity is linearly related to the path length, which is much smaller than the theoretical | S|=traversal of millions of nodes. In addition, since once the destination is set, the entire itinerary will not be recalculated frequently and completely, and the global planning is usually only re-planned when it deviates from the route or the road is closed ahead, so the T is very small, and most of the time it can be partially adjusted along the established route. Local behavior decisions are based on the current road conditions and the overall route to determine short-term driving actions, such as lane change, overtaking, deceleration and avoidance, etc. This is more complicated because the behavior of other dynamic agents needs to be taken into account, and the decision is game-based. Generally, unmanned vehicles use state machines + rules or policy networks to achieve this. The state machine rules select the corresponding strategy according to the scenario (slow train ahead, manned merging, etc.), which is equivalent to limiting a finite number of behavior modes, so the complexity of the decision is low (matching conditions + executing predetermined actions). The other is a strategy network trained with deep reinforcement learning, which inputs environmental features and outputs a continuous sequence of steering acceleration actions or strategies. This is inferred at O(1), but the training process is extremely complex, constantly optimized (done offline) in simulations and a large number of experiments. Motion control is a set of algorithms that convert the goals of the upper-level decisions (such as target speed, turning angle) into the underlying execution (throttle, steering wheel angle), usually through the optimization solver for fast calculation. For example, given the expected trajectory in the next 2 seconds, the control amount per 0.1 seconds is calculated by using model predictive control (MPC). This involves solving a constrained optimization problem with dozens of variable dimensions, which modern QP/LP solvers can accomplish in tens of milliseconds. Motion control complexity can often be thought of as constant time, because it is a fixed-dimensional optimization, and there is no calculation of how much it increases with the size of the environment. On the whole, the difficulty of the intelligent layer of unmanned vehicles lies in interactive decision-making: reasonable decisions need to be made in complex traffic scenarios, which may need to consider the future intention of multiple agents, that is, a multi-agent planning problem, and its theoretical complexity is prone to exponential explosion. However, the real-world system greatly reduces this complexity by means of stratification (global first and then local), decomposition (hypothesis interaction with each neighboring vehicle individually), and prediction (using vehicle dynamics constraints to reduce the likelihood). For example, if the system assumes that other vehicles obey traffic rules and have a limited number of typical behavior patterns, the vehicle only needs to perform a small number of branch evaluations of these assumptions, rather than exhausting all combinations of actions. Therefore C_W is kept within the practicable range. In extreme cases, there are still tricky scenarios (such as the need to merge lines in dense traffic), and the intelligent layer may not be able to do complete planning, and can only adopt a gradual heuristic strategy, which is equivalent to breaking down a major problem into multiple small action sequences to complete it step by step, so as to avoid computational of super complex solutions at one time. This exemplifies the application of human driving experience in AI: the approximation of large decision-making problems through rules and experience. In the future, with the progress of multi-agent game decision-making algorithms, more systematic and efficient decision-making methods may also emerge, which are currently dominated by heuristics and experience.

P-layer (intent): The top-level intent of an autonomous vehicle is usually simple and clear – to transport passengers from the starting point to the end point, while meeting safety, regulatory and efficiency requirements. This primary destination does not change during the journey (unless the passenger changes destination halfway, which can be seen as a target switch T=1). As a result, the intent layer introduces little to no runtime complexity compared to continuous decision-making and perception. A car does not need to select tasks by itself (tasks are given by the user), and there is no multi-task scheduling problem. Of course, at a broader level, if we consider the fleet of unmanned vehicles or the transportation system as a whole, there is the problem of intent coordination: for example, a group of unmanned vehicles collaborates to optimize the overall traffic flow, which requires the sharing of intentions (destinations, routes) between vehicles to avoid congestion, and there may even be a central coordination platform to dynamically allocate route resources. This is an intent coupling between multiple agents, and the complexity depends on the communication and coordination algorithms. Generally, city-level traffic scheduling is an NP-difficult optimization problem, but it can be scheduled regularly using approximate algorithms. Here we focus on the perspective of the bicycle, so we will not expand on it. For bicycles, the intent layer is more of a response to external commands: passengers change their destinations, traffic authorities issue instructions (temporary control requires diversion), etc. When these occurrences, the vehicle needs to re-route and behave, which is equivalent to triggering an intent switch T=1 and then running according to the new target. Each re-planning involves path recalculation, local decision update, etc., and the overall overhead is not large, which can be regarded as the complexity borne by the intelligent layer. It's like a person driving a car that suddenly changes lanes and needs to rethink the route, but it doesn't have much additional burden on the driving execution. In the same way for unmanned vehicles, the impact of target switching on complexity is absorbed through rapid planning. Therefore, we can assume that the overall complexity of C_P bicycle is almost zero (which occurs infrequently, and the cost is also reflected elsewhere when it occurs). In summary, the top-level goal of the unmanned vehicle system is stable and clear, and the intent layer will not become a bottleneck.

Summary of Optimization Paths: Layer complexity optimization is critical for autonomous unmanned systems, as the system must operate in real time under both computational and physical high pressures. Summarize the main optimization strategies:

Data Layer: Sensing Strategy Optimization – Reduce redundant data acquisition and reduce N with event-driven, area-filtering, and hardware filtering.

Information layer: Hardware acceleration and model optimization: Deploy high-performance computing chips, design lightweight and high-precision models, and use multi-task learning to reduce repetitive calculations. At the same time, the division of labor of multiple sensors is reasonable, and the secondary sensors are discarded if necessary to reduce the burden.

Knowledge layer: Preload key knowledge - high-precision maps and model parameters are loaded in advance, and only local updates are maintained locally to avoid real-time large-scale queries. and cloud sharing, where the cloud is responsible for complex knowledge calculations (such as global route optimization) and simple query results on the vehicle side.

Wisdom layer: hierarchical decision-making - global and local separation, short-term and long-term dismantling; Heuristics and learning are used together: use rules to constrain space, and use learning to make up for the limitations of rules; Parallel simulation – a limited number of strategies are evaluated in parallel rather than a single exhaustive attempt; Safety simplification - it is better to be conservative than to do high-risk complex strategies (for example, choosing to stop and avoid in uncertain situations is equivalent to avoiding solving complex combination problems and exchanging safety for efficiency).

Intent layer: target stability – unless it is necessary to change tasks infrequently; Collaborative planning - In the multi-vehicle system, the AI deployment intention of the upper traffic management is introduced to reduce conflicts and ineffective detours.

Through these measures, autonomous unmanned systems can achieve quasi-real-time and highly reliable operation in complex environments. As you can see, the DIKWP model helps us locate the complexity challenges layer by layer and propose countermeasures.

Case 3: Complexity analysis of a multimodal large model platform

Scenario description: A multi-modal large model platform refers to a large-scale AI model or system that can process multiple modal data (text, images, audio, video, etc.), such as a general artificial intelligence assistant with vision and dialogue capabilities. Such platforms usually consist of multiple large models (such as vision transformers, language models, speech recognition synthesis models, etc.) working together, or a unified multimodal model. Let's take an AI assistant that can read a picture conversation as an example to analyze its complexity.

Layer D (data): The multimodal platform accepts multiple input data at the same time, such as the user's text dialogue, uploaded pictures, voice commands, etc. The complexity of the data layer is reflected in the need to process data from different sources in parallel, sometimes with large amounts of data (e.g., high-resolution images, long speech audio). Let's say you upload a 4K resolution image (about 12 million pixels), and then add a 10-second voice (16kHz sample, 16-bit, about 160k sample), along with a 100-word text description. The total amount of this raw data is tens of megabytes of N. The platform needs to receive these data separately and do preprocessing, such as image compression/scaling, audio noise reduction/encoding, etc. These preprocessing operations are done at the data layer, and the complexity is roughly linear to the size of the data, i.e., $C_D = O(N)$. Considering that large model platforms are usually deployed on servers with abundant computing power in the cloud, it is affordable to process such a large amount of data in a single session, and the magnitude of N is not as demanding as that of real-time systems. The real trouble is that when user requests are frequent and a large number of concurrent data traffic soars, then the complexity of platform IO and preprocessing is obvious. Therefore, in terms of design, the size of the input data for each session will be limited (for example, the image cannot exceed a certain resolution, and the audio cannot be too long) to control the N of a single processing. In addition, for duplicate or similar data, caching can be enabled to avoid re-preprocessing. In general, although the complexity of the data layer is intuitively high in the large model platform (because the multimedia data is large), the cost of these IOs and simple preprocessing is not a major bottleneck compared to inference computing. After all, the transfer and initial processing of tens of megabytes of data is a small amount compared to billions of calculations in subsequent models. Even so, it still makes sense to optimize N to reduce the load on the system, such as uniformly compressing images to 1080p, uniformly converting voice to low bitrate, etc.

Layer I (information): The information layer is used in a multimodal platform to convert data from different modalities into representations that can be processed by the model. Typical steps include: tokenization of the text into a token sequence; The image is extracted into feature vectors by convolution or visual Transformer; Convert speech into text or extract speech features through speech recognition models. In modern multimodal models, these steps are usually done by specialized deep learning models, such as the Clip model, which maps images to text embedding spaces, and the ASR (Automatic Speech Recognition) model, which converts speech into text. In terms of complexity, these are deep model inference, which is computationally intensive. For example, a Transformer encoding 100 words of text may require hundreds of millions of floating-point operations. It takes billions of operations to extract an image feature from a ResNet. Fortunately, these model inferences are generally contained in the "big model" as a whole, and we can see that the boundary between the information layer and the knowledge layer is somewhat blurred: if the end-to-end multimodal Transformer is adopted, then the inference is directly input from pixels and characters, and the intermediate information extraction is implicit within the network, and the complexity is not calculated separately. But with a modular design, these perception models are the primary compute consumption of Layer I. Therefore, it may be quite high in this system, close to or even exceeding. For example, the Clip model processes a picture and a sentence of text, and the complexity is about (n, m is the number of image and text tokens), which is quite considerable. However, multimodal dialogue often requires multiple times of extracting image features or generating text embedding (e.g., aligning image features with new dialogue text repeatedly in each round of dialogue), which is further improved C_I accumulation. Layer I is optimized mainly by sharing representation and caching: if the same image is used multiple times in the same session, you can only extract features for the first time, and use cache embedding directly next time, instead of running the visual model. For example, the text obtained by speech recognition can be cached for use by the language model, so that the audio does not have to be re-identified every turn. There is also a multi-modal co-coding technology, which can process multiple modalities in one model at the same time, avoiding the multiple overheads of independent extraction and then fusion. However, this is often pushed to a larger model, and the complexity is still there. In short, the layer I complexity in multimodal systems is mainly determined by deep model inference, and there is no simple linear method to reduce it, but only to rely on model efficiency improvement and reuse of results.

K layer (knowledge): The knowledge layer of the multimodal large model platform is represented by the knowledge contained within the model and the external knowledge base. Take the popular large language model (LLM) as an example, which implies a large number of knowledge parameters; In conjunction with retrieval enhancement, the system will also connect to a knowledge base (such as a vector database or knowledge graph) as an external knowledge supplement. Knowledge layer complexity involves two parts here: internal knowledge invocation and external knowledge retrieval. Internal knowledge invocation refers to the complexity of the calculation of model parameters - this is actually integrated into the model inference overhead, which can be regarded as the intelligence layer. External knowledge retrieval, for example, retrieving relevant documents in a vector database when answering a user's question. The complexity of vector retrieval for database entry K is usually or depends on the index structure. If the system has a large knowledge base (e.g., 10^7 documents), retrieval may be a significant cost, but with pre-built indexes (e.g., HNSW graphs), results can generally be returned within tens of milliseconds. Therefore, compared to the time of model inference in seconds or even ten seconds, this retrieval is negligible. Therefore, the main part is still integrated into model inference. It should be noted here that knowledge graph inference is sometimes introduced in multimodal dialogue systems, such as replacing LLM inference with a logical reasoning module for user-relational problems, which involves another type of knowledge layer overhead. However, such systems usually do not invoke complex inferences frequently, and only target specific types of problems. Therefore, on the whole, the multimodal platform embeds a large amount of knowledge into the model in the form of parameters, which reduces the explicit processing steps of knowledge, in exchange for the problem of a large number of model parameters and slow inference. This trade-off shifts complexity from knowledge retrieval to intelligent reasoning (model computation). Therefore, it can be considered small and much larger.

Layer W (intelligence): The intelligence layer is embodied in the multimodal platform as a model inference process, that is, the process of synthesizing multimodal information and knowledge to generate answers or perform operations. Conversations, for example, are large language models (or multimodal models) that reason and generate based on the input context. The complexity of this process is the highest part of the whole system, because the current large-scale model parameters are tens of billions, and massive matrix operations are required for inference. In addition, if a longer answer needs to be generated, it also involves autoregressive step-by-step output, and each token repeats a large calculation. As a rough estimate, a 175 billion parameter Transformer model (such as GPT-3) will perform a multiplicative addition (assuming that the number of parameters is the magnitude of the calculation), and if 100 words are output, this amount will be multiplied by 100, plus multimodal processing, thousands of token inputs, etc., the overall amount of computation is very large. Although there is GPU parallel acceleration, the time is still measured in seconds or even longer. When there are many concurrent users, this becomes a significant bottleneck. Therefore, the complexity of the intelligent layer of the multimodal large model platform may be several orders of magnitude higher than that of other layers. Optimization is also a hot topic in the current AI field, including model distillation (using small models to approximate large models to reduce computation), sparse models (only some expert parameters are activated at a time to reduce computation), and caching contexts (for static and unchanged contexts, the Transformer layer is not repeatedly calculated). There is also a way to crop long sequences: for example, for long texts, only key sentences are taken and provided to the model through retrieval, so as to avoid feeding the entire large article. These methods can significantly reduce the inference complexity, but at the same time, there is a trade-off between reduced effectiveness. Another perspective is asynchronous pipelines and distributed parallel processing in the architecture, splitting a single inference to multiple devices to complete in parallel, which can also be regarded as an extension (although it does not change the progressive complexity but increases the throughput). Based on the current technology, the complexity of the intelligent layer of the large model platform is still mainly driven by the model size and sequence length, and the room for improvement is limited, but with the optimization of algorithms and hardware, the unit computing efficiency is improving.

P-layer (intent): The intent layer of a multimodal AI assistant has two aspects: user intent understanding and the system's own goals. User intent understanding refers to the system understanding what the user really needs, which is usually part of the conversation model, and is inferred through semantic analysis or conversation management algorithms, such as determining whether the user is asking a question or executing an order, consulting or small talking. This process is not very complex, which is equivalent to classifying or filling in the slots of conversation history, and can generally be implicitly completed by the model or judged by simple rules (such as detecting whether a sentence contains a question, etc.). The system's own goals are fixed in this scenario: to complete user requests, keep conversations interesting, and adhere to security guidelines (no violations). These targets are written into a dialog protocol or incorporated into the model input as prompts. The model attempts to meet these goals at the same time when generating responses. Intent layer complexity may be more reflected in the strategy of multi-objective trade-off, which is used in LLM to align the training process and integrate multiple objectives (correct, useful, and harmless) into the model through human feedback reinforcement learning (RLHF). This training phase may require a lot of simulated dialogue and optimization, and is an offline and highly complex process. But at runtime, the model already implicitly balances these goals and doesn't need to be explicitly scheduled. As a result, online C_P is extremely low, with no explicit target switching or task scheduling. Some platforms may allow users to switch modes (chat mode, creative mode, etc.) as an attempt to modify the behavior of the system, once the switching model uses different parameters or prompts, but the impact of this switch on the computation is only to load different weights or configurations, and does not involve highly complex calculations. As a result, there is little to no impact on overall performance.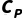

Summary of optimization paths: The multimodal large model platform concentrates most of the complexity on model inference (intelligence layer), and the relative weight of other layers is reduced by parallel or weakening. The main theme of optimization is also to reduce the cost of model inference, while coordinating the additional overhead brought by multimodality:

Data Layer: Input Management - Limit the size and frequency of a single input, such as image compression, audio duration limit, to control N.

Information Layer: Efficient Multimodal Coding – Use a unified model or a shared part of the network to process multimodal inputs, avoiding independent full computation of each modality. At the same time, the cache reuses the results of the previous step, such as image embedding, which is reused in the conversation.

Knowledge layer: retrieval enhancement instead of parameter memorization - for questions and answers that require detailed knowledge, instead of expanding the model parameters, external retrieval should be introduced, and the overall calculation may be lower-order; At the same time, the search index is optimized to speed up the query.

Intelligent layer: model compression and sparsity - distillation of small models, or use MoE sparse activation technology to reduce the amount of computation each time; Optimize inference algorithms, such as Int8 quantization acceleration, compiler optimization operators, and improve hardware utilization; Reduce redundant computation – Use a memory mechanism for long conversation contexts to avoid recoding the entire history each round.

Intent layer: alignment preprocessing - the multi-objective balancing problem is solved in the training stage, and the decision-making is simplified at runtime; Low cost of mode switching - pre-load different mode models into memory, no need to wait for a long time to load or compute when switching.

Through these efforts, multimodal large model platforms are becoming more practical. However, it is still many orders of magnitude more complex than traditional purpose-built systems, which is at the cost of its high functionality. The DIKWP analysis helps us see that the system concentrates almost all of the complexity at the inference layer, because it chooses an end-to-end model learning approach to reduce manual stratification and knowledge engineering. There are pros and cons to this "computing for knowledge" approach: it is flexible but resource-intensive. The future direction may be to combine the two, which not only introduces explicit knowledge to reduce the inference burden of the model, but also retains the generalization ability of end-to-end learning to achieve a better complexity balance.

Cutting-edge concepts and semantic complexity quantification frameworks

In the analysis of complex intelligent systems, in addition to the traditional complexity quantification, some cutting-edge concepts have begun to show their importance, such as semantic elasticity, relative complexity of subjects, semantic space flow, etc. These concepts focus on measuring complexity from a semantic and subject perspective, giving us richer insights than just computational quantities. The following introduces each of these concepts and discusses their quantitative frameworks, as well as how they can be incorporated into the DIKWP complexity analysis system.

Semantic elasticity

Definition: Semantic elasticity refers to the flexibility and robustness of a system to process and represent semantics. Specifically, it describes the extent to which a concept, proposition, or command allows for a variety of expressions that can still be recognized as equivalent by the system, and the system's ability to face semantic variations (e.g., inputs with different wording, different forms, but similar meanings). Systems with high semantic elasticity can "stretch" their semantic comprehension categories and are adaptable to semantic noise, ambiguity, or metonymy. Systems with low semantically elasticity require strict formats or specific patterns to understand meaning.

Significance: In artificial consciousness and cognitive systems, semantic elasticity is directly related to the generalization ability of the system and the natural interactive experience. For example, humans have a high degree of semantic flexibility in communication: a sentence can be understood in a different way or with a different accent. However, many traditional AI systems are very sensitive to input formats, and the slightest change may not be parsed. This means that the lack of semantic elasticity artificially increases the complexity of the system: it is necessary to exhaust every possible format or to strictly regulate input. Improving semantic resilience is equivalent to simplifying the complexity of human-computer interaction through smarter understanding.

Quantification Framework: How to Measure Semantic Elasticity? One idea is to characterize the distance between different representations of the same semantic content and the system's tolerance for that distance. Specific steps may include:

Determine a set of baseline semantic content (e.g., specific intents or concepts) and generate a number of different expressions of them (different wordings, forms, multimodal representations) to form semantic equivalence classes.

For each equivalent class, the measurement system handles the various representations consistently within it. For example, see if the system outputs are the same or if the semantic representations are in the same class.

Semantic elasticity can be expressed in terms of the success classification rate or the semantic retention rate: if the system can recognize X% of the variants as the same semantic, the elasticity is high. If there is a slight change and the identification error is made, the elasticity is low.

Another type of quantification: introduce a semantic difference measure (such as editing distance, embedding distance, etc.) to represent the apparent difference degree of two expressions, and find out the maximum difference range of the system understanding results to be consistent, which is called semantic tolerance ε. If the difference between the two expressions is less than ε, the system will process the result equally; greater than ε is not equal. This ε can be used as a scale of semantic elasticity: the larger the ε, the more tolerant the system is to change.

Mathematically, each semantic equivalence class can be thought of as a "region of elasticity" in the semantic space. If any point (representation) in the region is mapped to approximately the same output, the region is covered by the system. A resilient system covers these areas continuously and connectedly, while a less resilient system covers only a few discrete points. We can borrow from the concept of set coverage: assuming that there is an ideal continuous spatial measure Vol(class) for each equivalent class, and the system actually covers Cover(class), then semantic elasticity can be expressed by coverage. Obviously, the ideal elasticity is 100% coverage, and in reality, the higher the better.

Role in DIKWP analysis: Semantic elasticity can be seen as a moderating factor for the complexity of the information layer and the knowledge layer. High semantic elasticity means that the system does not need to process each input format separately, and can handle the deformed input with a unified semantic representation, thus reducing the complexity of the information layer to distinguish branches. For example, if a natural language understanding module is highly flexible, whether the user says "turn on the living room light" or "turn on the living room light", it is mapped to the same intent representation, which avoids the redundancy of treating these statements as different situations. This is equivalent to reducing complexity by normalizing semantics. Therefore, an elasticity coefficient can be introduced into the complexity formula, so that the effective complexity multiplied by E reflects the calculation savings due to the increase in semantic elasticity. As in the previous information layer formula, if the system has the flexibility to deal with repetitive forms, then it will actually be reduced, because similar content can be processed uniformly.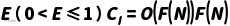

Another dimension of semantic elasticity is robustness: the ability to guess semantics for noisy or incomplete information. This can be seen as part of resilience. Quantification of robustness usability performance degradation curve: Measure the degree to which the output of the system remains correct by gradually increasing the input noise. The area under the curve can be used as an indicator of robust elasticity.

In summary, semantic elasticity emphasizes the ability of complex systems to adapt to change and diversity at the semantic level. Increasing resiliency often means increasing complexity in the design phase (requiring smarter algorithms) but decreasing in the use phase (no additional branching logic required to handle diverse inputs). Therefore, in the DIKWP model methodology, semantic elasticity is an important implicit complexity reduction mechanism: through the intelligent processing of semantic variants, many cases that should be handled independently are merged into one. In our analysis framework, we should consider incorporating semantic elasticity into complexity assessment, for example, when assessing the overall complexity of the information layer or interaction, a highly resilient system can assign a "complexity discount", and vice versa.

The subject is relatively complex

Definition: Subject-relative complexity refers to a measure of complexity that should not be viewed in isolation from the task itself, but rather by who is performing or understanding the task. Different subjects (which can be different agents, people with different levels of experience, and different AI models) have different knowledge and capabilities, and the same task presents different complexities to them. This concept stems from the idea of "relativism of consciousness": each agent's path to perception and understanding of complexity is subjectively relative, and there is no absolutely uniform semantic structure. In short, complexity must be measured in terms of the subject-content relationship, not the content itself.

Significance: In AI assessment, the relative complexity of the agent reminds us that easy/difficult is relative to the agent. A task that is simple for humans can be extremely complex for current AI, and vice versa. For example, recognizing a photograph of a common object is effortless for a human, but it can be complicated for a small neural network. Similarly, solving an advanced mathematical proof problem is extremely difficult for the average person (high complexity), but for a trained theorem proving the AI may be able to complete it in a reasonable amount of time (less complex for it). Therefore, when designing and analyzing complexity, it is necessary to clarify the subject benchmark. If we consider the artificial consciousness system as subject A, the complexity of a task X; However, for human expert subject B, the task may be of complexity Y(Y≠X). This difference should be taken into account methodologically. For example, when evaluating general AI, it is necessary to avoid the trap of "pure objective complexity": seemingly simple questions may stump the AI because the AI lacks human background knowledge. The relative complexity of the subject also illustrates the role of learning and experience: through learning, the subject's internal knowledge increases, simplifying many otherwise complex problems for him. This could explain the correlation between intelligent growth and complexity reduction.

Quantitative Framework: How to quantitatively describe this relativity? The intuitive approach is to use the concept of conditional complexity. Reference can be made to the conditional Kolmogorov complexity: the shortest encoding length required to describe the information x for a given knowledge/model of subject M. Here subject M can be abstractly expressed as a compressed description of its existing knowledge or ability. The smaller it is, the easier it is to describe (i.e., the simpler) the information x is for subject M. For example, for subjects with rich knowledge of physics, complex physical phenomena x can be summarized by concise models, small; For subjects who don't understand physics, they can only memorize and observe data pixel by pixel, which is large. Therefore, you can use as one of the complexity metrics. As another example, in a Q&A task, you can define complexity as the amount of new information required for the answer = I(answer|subject's knowledge). If the subject already has relevant knowledge, there is little new knowledge that needs to be introduced (low complexity); If the subject has no knowledge of this domain at all, he or she will have to learn a lot of new knowledge to solve the problem (high complexity).

Another framework is the subject-problem matrix: suppose we have a set of problems and a set of subjects, we can build a matrix M, where the agent can solve the problem efficiently, and =0 means cannot. The traditional complexity of a problem is to see how many agents can solve it (or how long it takes to solve it). However, the relative complexity of the body emphasizes the distribution of one column for each S_j. For example, problem i is easy for subject A and difficult for B. This matrix is actually a knowledge/skill coverage matrix. If we map the subject's knowledge background to a feature space, we can try to construct a complexity function, which is a certain representation vector of the subject's knowledge state, and a task can be represented as a set of required knowledge points, then the complexity function can be defined as the degree of difference between the knowledge required by the task and the existing knowledge of the subject. For example. The greater the overlap (the more the subject knows to cover the task requirements), the lower the complexity is close to 0; The smaller the overlap, the more complex it is close to 1 (or infinity means it can't be done). This measurement needs to be able to formalize and compare subject knowledge and task requirements. For example, in the DIKWP framework, the complexity can be defined by the degree to which the DIKWP map of the subject matches the DIKWP subgraph related to the task. If the matching is complete, the task has almost no complexity increment for the subject, and if the matching degree is low, a new DIKWP link needs to be built (high complexity).

Role in DIKWP analysis: The relative complexity of the subject requires us to always clarify what the knowledge state (K-layer content) and ability (algorithm-strategy W-layer) of the subject are when analyzing the system complexity. Especially in multi-agent systems, the complexity of each individual is perceived differently, which affects the efficiency of collaboration. Therefore, subjective perspectives need to be taken into account when coupling complexity analysis. For example, if two agents exchange information, if they have different knowledge backgrounds, they must explain the context, and this interpretation process itself adds complexity. Incorporating this factor into the analysis allows for a more accurate estimation of communication overhead, among other things. Quantitatively, we can give a subjective and objective complexity conversion formula: Suppose raw task complexity (from omniscient view) = C0, subject knowledge coverage = p (0 to 1 fraction), then the actual perceived complexity of the subject. When p=0 , the subject has no relevant knowledge, complexity = C0; p=1 The subject is omniscient, and the complexity is close to 0. Such a formula, of course, is sketchy, but expresses a linear relationship hypothesis. In fact, it may be an exponential or threshold effect, that is, it is almost impossible to complete without mastering the key knowledge points.

The relative complexity of the subject also leads to the concept of uncertainty or incomparability—the complexity of different subjects cannot be simply compared because they have different frames of reference. This is similar to the theory of relativity in physics: you can't talk about absolute motion, you can only say motion relative to a reference. In the same way, there is also a lack of absolute zero in complexity. Therefore, when evaluating the performance of an artificial consciousness system, it is necessary to specify a reference (usually based on a human expert, or a standard AI) and then say that "the system is 80% human, so the complexity of looking at task X is roughly equivalent to the complexity value Y that humans perceive." This idea of relativism led us to introduce benchmarking tasks and benchmarking bodies to calibrate the complexity scale. For example, the Turing test or other benchmarks can be used to compare the performance of AI and humans on the same task, so as to infer the subjective complexity of AI.

In conclusion, the relative complexity of the subject reminds us that complexity is not an objective constant, but depends on the knowledge, experience, and intelligence of the cognitive subject. In the practice of DIKWP methodology, we should dynamically adjust the complexity assessment through the host model (such as the DIKWP graph). For example, when a system expands its knowledge graph through learning, the complexity of the tasks it faces should be reduced because many of the problems become easier for it. This also gives a measure of complexity evolution: if the system continues to learn, does its effective complexity decrease over time? This can be used as a measure of intelligent progress. As the ideal AI increases with experience, the perception of the complexity of the same environment continues to decrease, and it becomes more and more comfortable.

Semantic space flows

Definition: Semantic space flow refers to the process of semantic content being transmitted and transformed between different representation spaces or subjects, as well as the fidelity and change of semantic information. Here, "semantic space" can refer to the semantic representation of different layers (e.g., from the data space to the knowledge space) or the internal semantic representation of different subjects. Flow describes the dynamic process of semantics starting from one space and arriving at another space through transformation, including encoding, decoding, translation, inference transfer and other steps.

Meaning: In complex systems, information and meaning often need to flow between multiple levels and modules. For example, a concept has different forms in the linguistic and visual areas of the brain, but a person can turn visual images into verbal descriptions – this is the flow of semantics in different areas of the brain. Another example is two AI agents, each with its own internal semantic representation system, which needs to exchange information through communication protocols, and the semantics are mapped from the knowledge space of one agent to the communication signal, and then to the knowledge space of the other. If there is a loss of semantics or ambiguity in the process of circulation, it will lead to misunderstandings and errors. The efficiency and accuracy of semantic space flow determine whether the system can be effectively coordinated and operate correctly. It can be said that complex systems must not only deal with semantics at each layer, but also transfer semantics correctly between layers and subjects and subjects. The difficulty lies in the fact that each space is represented differently (formal notation vs vector embedding vs graph structure, etc.), and each transformation can introduce uncertainty or loss of information.

Quantification framework: The effect of semantic space flow can be measured by semantic equivalence and attrition. Specifically, you may consider:

Define the semantic representation function for each relevant space, and the transformation channel to represent the transformation operator from space A to B.

For a given semantic content x, it is expressed in space A as. The representation in B space is obtained by transforming the operator T. Let's look at the semantic content corresponding to y (mapped back to the actual semantics).

If (or equivalent to x within tolerance), then the flow is lossless. Otherwise, there is a loss of semantics or an error of Δx.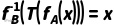

Quantitative metrics can be semantic fidelity: for example, using a contracted semantic similarity value between 0 and 1. 1 means perfect fidelity, and close to 0 means almost no semantics.

Another metric is information efficiency: how much additional information is needed to reconstruct x in B. If the T conversion is insufficient, additional supplements need to be sent to restore x. This additional amount of information can be measured as the information entropy of the untransmitted part from the perspective of mutual information.

These indicators are applied to various layers of transformation: such as the semantic flow efficiency from data to information, and the semantic execution efficiency from knowledge to intelligent decision-making to action (intention space); Or it can be used for subject communication: Agent1 converts semantic X into message m, Agent2 receives m and interprets it as Y, and compares the difference between X and Y to obtain the fidelity score.

Semantic flow often inevitably has irreversible parts, such as continuous perception - > discrete symbols lose detail. The fidelity < 1 in this case, but the important thing is whether the key semantics are compromised. Weighted fidelity can be calculated by weighting key semantic elements (e.g. the main semantics are correct but the details are wrong, and most of them can be considered retained).

Role in DIKWP analysis: The concept of semantic space flow provides a measurement tool for the complexity of interlayer coupling. If the semantic transition between two layers is inefficient, then the complexity is amplified between the layers - because the information obtained by the later layer is incomplete and needs to be compensated for by additional reasoning or multiple rounds of feedback. For example, in a natural language dialogue system, the user's intention (intention space) is expressed as an utterance (information layer) and transmitted to the AI, and the AI may misinterpret part of the semantics, which will lead to multiple rounds of clarifying the dialogue to make up for the missing meanings, increasing the overall complexity. If you understand it accurately the first time, the complexity is significantly lower. Therefore, improving the efficiency of semantic flow (through better coding, protocol, and collaborative training) directly reduces the complexity of interaction. We can think of inefficient semantic flow as introducing a complexity penalty term: for example, in the previous total complexity C_total formula, add a term λ * (1 - fidelity) to represent the additional complexity caused by the loss of semantic flow. Fidelity = 1 No penalty, low fidelity means high penalty.

In addition, the complexity of multi-agent collaboration depends largely on the flow of semantics: if the agents share semantic standards (high-fidelity communication), the complexity is close to the level of the smartest person in the team to complete independently; If communication is difficult, the complexity can skyrocket or even escalate to the point where each is trying to figure it out. This available comparison experiment shows that multi-agent teams with shared language vs. no shared language perform differently when completing tasks. Quantitatively, if each communication has fewer bits or a high error rate, more rounds of communication (= greater T, L in P) are needed, and the complexity is multiplied by the number of feedbacks. Therefore, the reciprocal of the flow efficiency is almost proportional to the complexity of the intent layer.

A framework can refer to semantic communication theory and collaborative entropy. Semantic communication seeks to convey useful semantics rather than byte-by-byte, which can significantly reduce the amount of traffic while maintaining the necessary semantics. This is essentially an optimization of semantic flow. Measure the definable semantic compression ratio = original data bits / semantic bits used. When this proportion is high, it indicates that the flow mechanism cleverly discards irrelevant details, retains semantics, and greatly reduces the amount of data. For example, when we tell a story to a child, we don't read the essay verbatim, but condense it into easy-to-understand language. This reduces the receiver complexity while preserving the semantic core and having a high semantic compression ratio.

In summary, semantic space circulation emphasizes the quality of semantic transmission across layers and subjects. The quantification framework revolves around fidelity and efficiency. Incorporating this into the DIKWP Complexity Methodology, we can:

Analyze the semantic fidelity of each adjacent layer transformation and identify complexity bottlenecks. For example, if too much context is lost in data-> information, the intelligence layer will have to be tested repeatedly (the equivalent complexity increases).

Optimization strategy: Design better representations and protocols to improve fidelity or achieve high enough fidelity with fewer resources, that is, maximize semantic information utilization.

In the multi-agent coupling complexity model, the semantic flow coefficient is introduced to represent γ communication quality, and it is evaluated in combination with task complexity and agent ability. For example, the total complexity is $ ~ C_single/γ if agents share load via communication$. Low γ is inefficient.

With this convergence effect, our complexity analysis will not only look at the number of steps, but also focus on the semantic work. After all, if you don't understand the semantics of 10 million steps, the complexity should be reflected in the cost of effectively achieving the goal. This measurement is complemented by indicators of semantic flow.

Integration of cutting-edge concepts in complexity analysis

Integrating the above concepts into the complexity analysis system requires a multi-dimensional quantitative framework. We can envisage an extended traditional complexity representation O(f(n)) of the form of , which contains, in addition to the main problem scale n, the following:

E (Elasticity) is a semantic elasticity parameter, which corresponds to the semantic generalization ability of the system, and E high can be reflected in the complexity function as the effective input scale reduction or state space reduction. For example, treat n equivalent inputs as one.

Rel(Relativity) subject-related parameters, such as subject knowledge coverage p or ability level L, are used to adjust the complexity order or coefficient. For example, in the previous example, this complexity may be marked as "difficult" for low-ability subjects and "easy" for high-ability subjects.

\Phi (Phi or other symbols) semantic flow efficiency parameters, which may include communication fidelity r, semantic compression ratio c, etc. This can be reflected in interlayer coupling terms or the number of additional cycles, such as complexity multiplied by 1/(rc) because inefficient flows take several times to repeat.

Through this parameterization, complexity analysis is expanded from a single scale function to a comprehensive model considering semantic quality and subject factors. This is especially necessary for cutting-edge AI systems, where semantic intelligence (resilience, communication, learning) is itself a core factor in complexity.

For example, for a cognitive system with a semantically elastic network, we can expect it to reduce computation through elastic merging when information is redundantly inputted, and its complexity growth tends to be more sublinear rather than linear. When there is no elasticity (processed one by one), it is strictly linear or even superlinear. Therefore, the effect of E is to decrease the slope from 1 to <1. If you want to give an academic form, you can write and α decrease with E increase. The limit E = 1 perfect elasticity and α->0 means that the input diversity does not add additional cost (theoretical perfect case).

For the subject relativity, we can introduce an agent complexity function, g represents the reducing effect of knowledge on complexity, the larger the K_subject g, the greater the complexity, and the greater the denominator, the less complexity. This may capture qualitative facts where experience can reduce actual complexity. This relationship is similar in machine learning algorithms: some algorithms converge faster (low effective complexity) and stochastic initialization (high complexity) when given a good initialization or prior. K_subject can be seen as a priori guidance. Quantitative analysis can try to establish an empirical curve, from zero experience to expert to draw complexity points, to see if the form of g can be fitted (such as logistic improvement, the accumulation of experience in the early stage significantly reduces the difficulty, and the later stage slows down).

The effect of semantic flow on complexity can be injected into the feedback loop model. As discussed earlier, if the fidelity is low and k-round communication is required, the complexity is ~k*C0. k can be approximated by 1/(1-r) (when a certain proportion of uncertainty is eliminated in each round), and r is the semantic ratio of each round. In this way C_total ~ C0 / (1-r). If r->1, C_total tends to be limited; r low C_total explosion. This formula holds up under certain assumptions, at least qualitatively illustrating the importance of improving r.

In conclusion, the integration of semantic elasticity, relative complexity of subjects, and semantic flow into complexity analysis is helpful to build a more comprehensive and practical complexity assessment framework. Traditional complexity theory ignores semantic factors, while in cognitive intelligence systems, semantic factors often determine the upper limit of system performance and actual computational requirements.

This multidimensional framework is important not only for analyzing existing systems, but also for designing new systems: we can radically reduce the computation and iterations required by the system by improving semantic elasticity, ensuring knowledge coverage, and improving communication protocols, thereby creating more efficient agents. In other words, the quantification of these cutting-edge concepts is not only a passive assessment of complexity, but also a design criterion for actively reducing complexity. When we see the complexity of a certain system exploding at a certain level, we may wish to check whether there is insufficient semantic elasticity or too much communication loss, and then prescribe appropriate measures to improve its structure.

Integration of DIKWP with mainstream AI frameworks

The DIKWP model provides a full-stack view of the composition and sources of complexity of intelligent systems. So how to combine this hierarchical semantic model with the current mainstream AI framework to give full play to their respective advantages? This section will discuss the integration of DIKWP with three main directions: large models with Transformer architectures, reinforcement learning paradigms, and multi-agent systems. The goal of convergence is two-way: on the one hand, the semantic layering of DIKWP is used to improve the interpretability and complexity management of these frameworks, and on the other hand, the DIKWP model can draw from the existing results of these mature frameworks and move from theory to application.

Fusion 1: DIKWP and Transformer large model

Background: The Transformer architecture and the various large-scale pre-trained models it has evolved from (e.g., BERT, GPT series, Vision Transformer, etc.) are at the core of AI breakthroughs in recent years. These models typically employ an end-to-end deep learning approach to learn implicit representations and knowledge from massive amounts of data. They have achieved amazing results, but there are also significant problems, such as poor interpretability, hallucinatory phenomena (the output of the model does not conform to the facts), and uncontrollable goals. These problems are essentially related to the explicit semantic hierarchy and the absence of intent representation that the DIKWP model emphasizes. For example, the Transformer model is implicitly mixed when processing the transformation of data-> information-> knowledge-> intelligence-> intent, especially the lack of explicit intent modeling, resulting in incomplete and inconsistent semantic transformation.

Fusion ideas: By introducing the structure of DIKWP into the Transformer framework, you can consider the integration of two aspects: the model structure and the surrounding process of the model:

Structural fusion: Through modular design, the Transformer model is divided into parts or matched with functional modules corresponding to the DIKWP layer. For example, add a dedicated "intent module" (P-layer) to the model to clearly guide the direction of the output. This can be analogous to introducing a planning head or control vector into a language model that represents the purpose of the current generation, thereby reducing aimless wandering and hallucinations. Recent techniques, such as adding a target description to a prompt or introducing chain-of-thought step-by-step inference, can be seen as giving explicit representations of part of the W layer (inference) and P layer (target) in the model to incorporate the DIKWP idea. In addition, it can be considered to split the model memory into a combination of explicit knowledge base (K-layer) and parameter memory, that is, to construct a retrieval-enhanced Transformer: for the required knowledge, it does not completely rely on parameter implicit learning, but retrieves the knowledge base in inference. This is exactly what the DIKWP approach promotes, where the knowledge layer is exposed as a knowledge graph or database to constrain and inspect the content generated by the model. This approach has been seen in some models, such as Realm and RETRO, which make the language model refer to external knowledge by retrieving documents, thereby reducing illusions and improving accuracy.

Process Convergence: Transform training and inference processes with DIKWP thinking. For example, staged training: the model is trained to complete D->I->K representation learning (e.g., self-supervised learning to obtain data-to-information and information-to-knowledge representation), and then K->W->P training (supervised learning inference and alignment intent). This is more targeted than end-to-end hybrid training, while each stage is more controllable and explainable. In addition, when inferring, the task is decomposed into DIKWP levels: for complex inputs, the model is used to extract key information (layer I output), then the knowledge reasoning module is used to process the complex logic (K->W), and finally the model generates language answers (W->P expression). This method of combining pipeline with large models can improve interpretability while ensuring effectiveness. For example, some recent systems use LLMs with symbolic reasoning: LLMs are used to understand the problem (D->I), then convert the problem into instructions that call the knowledge base or computation module (I->K->W), and the result is then generated by the LLM (W->P). This is a fusion of DIKWP hierarchy and Transformer capabilities, which apply the model's strengths (understanding language and generating utterances) to the corresponding levels, while handing over key reasoning to more reliable symbols or knowledge modules to achieve more accurate results.

Advantages: This convergence brings multiple benefits: (1) Interpretability improvement: When the model has explicit knowledge modules and intent control, it is easier for us to trace the source of error. For example, if the output is wrong, you can check whether the knowledge base is missing or the model is incorrectly referenced, rather than having a hard time knowing which layer is wrong as in a pure LLM. (2) Reduce hallucination: The knowledge retrieval module ensures that the model's answers are based on real data, while the intention module avoids the model from deviating from the user's questions. (3) Controllable complexity: The model deals with different problems at different stages, avoiding using the largest model to solve everything at the same time. For example, first use a small model or rule to solve the simple part, and then call the large model, and only enable the huge computing power when needed, which is similar to the division of labor by layers in DIKWP, and it is also a kind of Mixture-of-Experts idea. OpenAI's recent proposal to divide GPT into several specialized expert models to share tasks is a similar hybrid approach.

Implementation Challenges: Of course, there are challenges to integration. Part of the success of the Transformer architecture lies in its end-to-end training beyond human knowledge and layering, which automatically learns some implicit layering. We made it clear that new training algorithms and more data may be needed to ensure smooth connectivity between the modules. Moreover, the module division is not good, and it is easy to degrade performance or unstable training. Therefore, there are two poles in the current industry: one pole is biased towards a more end-to-end (such as directly letting the Transformer output decisions from the video pixels, everything is implicit), and the other pole is biased towards modules (vision module + language module + control module). The DIKWP idea clearly falls into the latter category. As the scale of the model grows, we may find that it is difficult for the pure end-to-end model to further greatly improve the controllability and reliability, and modularity is the general trend. DIKWP provides theoretical guidance for module partitioning, so that modules are no longer empirically segmented, but have clear semantic meanings. In practice, some explorations, such as transparent AI models and causal transformers, are trying to inject some kind of structure.

Overall, the fusion of DIKWP and Transformer is to gradually evolve the current powerful black box model into a white box model with an internal hierarchy. In the short term, it may not be realistic to completely dismantle, but the local fusion has already shown results. For example, when Microsoft Bing integrates GPT-4, it adds search engine retrieval (knowledge layer) assistance, which significantly improves accuracy, which is essentially the application of DIKWP ideas (using K layer to enhance the W layer inference of LLM). In the future, more similar cross-system fusions will emerge, so that large models can not only maintain strong representation learning capabilities, but also have the controllability and accurate knowledge of traditional symbolic AI.

Fusion 2: DIKWP and reinforcement learning

BACKGROUND:Reinforcement learning (RL) is one of the main paradigms for enabling intelligent autonomous behavior. Under the RL framework, the agent learns strategies based on state-action-reward feedback by interacting with the environment. Although the concept of classical RL is clear, when the state and action space are complex, the learning efficiency is often low, and a lot of trial and error is required. In particular, when traditional RL encounters high-dimensional perceptual inputs (such as images), it needs to be combined with deep learning to extract state features to form "deep reinforcement learning". Despite their success in areas such as gaming, RL agents are often seen as a flat black box, with opaque decision-making processes, heavy reliance on set rewards, and a lack of high-level semantic goals.

Convergence ideas: DIKWP can provide a hierarchical perspective for reinforcement learning, decomposing flat RL processes into different semantic layers, so as to improve learning efficiency and interpretability:

State Characterization (D→ Layer I): In RL, raw observations, such as pixels, are data layer inputs. It is often necessary to learn a state representation, which is the task of the information layer. DIKWP reminds us to focus on the extraction of meaningful information, rather than blindly letting the strategy network learn from pixels on its own. In practice, self-supervised learning or knowledge guidance can be used to pre-train state representations to turn observations into low-dimensional information that is meaningful to the task. For example, in autonomous driving RL, a supervised training model is used to identify lane markings and vehicles in the image, which is equivalent to building an information layer, and then the RL only needs to make decisions based on the extracted information. This is similar to humans, who first learn to recognize the environment and then learn to plan. Doing so reduces the state complexity of the RL because the transition from Layer D to Layer I has compressed the size of the state space. The D→I layer of DIKWP converges here in combination with feature engineering/representation learning and RL. Many of the current deep RLs do the same, such as the "world model" method, where an environment model (equivalent to K-layer or I-layer) is trained first, and then the strategy is optimized in the abstract space learned. DIKWP provides a clear framework for this step: policies should not be learned directly on the raw data, but should be layered.

Hierarchical decision-making (W-layer): Reinforcement learning can be divided into levels, such as hierarchical reinforcement learning (HRL), where high-level policies are set to determine sub-goals, and low-level strategies are set to achieve sub-goals. This corresponds to the different granularity decisions of the intelligence layer in DIKWP, as well as the sub-intent management of the intent layer. For example, in a navigation task, the top-level policy determines the next signpost target (the intent layer), and the bottom-level policy controls the specific action to make the agent reach the signpost (smart execution). The difficulty with HRL is how to break down subtasks and rewards. The DIKWP perspective can be assisted by the knowledge layer and the intent layer: use domain knowledge to predefine subtasks, or let the high-level strategy generate subtask descriptions (intents), and the low-level follow the intent optimization. This is similar to the options in RL. DIKWP suggests that knowledge representations should be explicit, such as building state-sub-target knowledge graphs to represent complex task structures. The RL agent can plan a rough route on the knowledge graph (similar to people using knowledge reasoning), and then use RL to execute it in each segment. This convergence allows RL to no longer rely solely on rewards to explore the global structure, and part of the structure is provided by knowledge. Some studies, such as FeUdal Networks and HER algorithms, also reflect similar ideas: the introduction of "target vectors" to guide low-level policies is equivalent to explicitly communicating a sub-intention to the low-level. This is really the P-layer interaction that gives the RL DIKWP.

Multi-agent and Learning (K-layer): Reinforcement learning agents form their own strategies (knowledge) in their interactions with the environment. DIKWP reminds us to focus on knowledge refinement and transfer: for example, abstracting learned strategies into generalizable knowledge that can be repurposed for new tasks. This can be achieved through meta-learning or strategy distillation, which is equivalent to elevating the intellectual outcome of one task to the knowledge layer content, and then accelerating the learning of the new task as prior knowledge. It's in line with human practice: having learned to ride a bike, mastering balance, and learning to skateboard is also helpful. Traditional RL is inefficient to learn from scratch, but if cross-task common knowledge can be stored in the K layer (such as value function approximation and dynamic model), the complexity of learning new tasks (exploration steps) will be much reduced. Existing methods such as "generic value function approximation" and "inheritance of old policy parameters" are all based on this idea. The DIKWP framework emphasizes knowledge graphs and relationships, and can also be used for RL: for example, abstracting states/actions in different environments into knowledge graph nodes, learning their relationships, and inferring the effects of new combinations. While this is cutting-edge, the direction is clear: to fuse symbolic knowledge with RL to accelerate policy learning and improve interpretability.

Reward vs. Intent (P-Layer): In RL, the reward function defines the agent's goal, but well-designed rewards are often difficult. DIKWP's intent layer can help provide a higher-level representation of the target. For example, inverse reinforcement learning or high-level instructions can be used to make agents understand human intentions, rather than figuring through low-level numerical reward curves. By incorporating intent into RL, you can generate a target condition policy: policy( state, goal), which can switch behaviors for different intents. In this way, the experience can be reused for different goals, and the learning efficiency is improved. In addition, multi-objective RL can also use intent-layer thinking: multi-objective is represented by weights, and then there is a high-level module that adjusts those weights (equivalent to constantly adjusting the intent preference), and the underlying strategy follows this adjustment optimization. When training, you may want to add an intent embedding vector input policy so that it learns to adjust its actions according to different intents. In this way, once you change the goal, you don't need to re-learn, as long as you change the intention vector, you can have a new behavior. This is similar to how conditioned models are generated.

Advantages: The integration of DIKWP and RL has the following advantages: (1) Improve sample efficiency: Through knowledge guidance, state feature extraction and hierarchical decomposition, RL does not have to blindly explore in the huge original space, which reduces the learning complexity. For example, DeepMind trains the manipulator to manipulate the robotic arm, first using teaching to learn low-level movements, and then using RL to learn high-level strategies, which is much faster than end-to-end, which is a victory for layering. (2) Improve robustness and generalization: With knowledge and stratification, agents are not easy to "forget" important structures and can apply knowledge to new situations, rather than starting from scratch every time. For example, if you have learned to walk the knowledge map of maze A, you can quickly navigate by changing maze B. (3) Explainable decision-making: A hierarchical strategy can output a sequence of high-level decisions (e.g., "go to A first and then get B") to make people understand their intentions, rather than just a string of low-level operations that are difficult to understand. Especially in robotics applications, this is critical to increase human trust.

Implementation Challenge: The need to reconcile the contradictions of symbolic knowledge and continuous control. RL mostly deals with continuous probabilistic strategies, and knowledge/intent is usually discrete symbolic in nature, and how to make the interface match between the two is a technical difficulty. In addition, hierarchies often require a priori, and automating the task is still a challenge. However, in recent years, the combination of combinatorial planning (symbols) and RL (learning) has begun to overcome these problems.

Typical results include the introduction of PDDL (AI Programming Language) into RL to solve complex tasks, so that RL only focuses on low-level actions, plans high-level sequences, and solves the learning of long-term tasks (such as 8 sub-task sequences). There are also studies such as the use of knowledge graphs to aid exploration, and there are studies to build knowledge for Atari games such as "the key opens the door", and RL uses this knowledge to significantly reduce the number of attempts.

In summary, the integration of the DIKWP framework and RL represents the combination of traditional symbolic AI and data-driven learning. It is expected to create stronger agents: those who can adapt through learning, and who have the knowledge and structure to act as a skeleton without blind movement. It's a lot like human cognition: we have prior knowledge and logic, and we can also adjust from feedback. It is believed that in the future, this kind of integration will be seen more and more in agent architectures, such as AdaPlan, recently developed by OpenAI, which uses large language models as the high-level strategy, and the underlying layer is executed by RL, which has a significant effect in game inference. DIKWP provides a clear blueprint for such a system, indicating the data, knowledge, or intent role that each module plays.

Fusion 3: DIKWP and multi-agent systems

Background: Multi-agent systems (MAS) are made up of multiple agents interacting with each other to collaborate or compete to accomplish a task. Research in this area includes distributed AI, game theory, swarm intelligence, etc. Multi-agents introduce a new source of complexity: interaction complexity. The complexity of traditional monolithic AI is no longer easy, and multi-agent also needs to consider communication, coordination, game balance, etc. Many current achievements, such as self-organizing swarms, auction algorithms, and MARL (multi-agent reinforcement learning), provide partial solutions. However, there are still challenges, such as the scale of coordination is not scaling, and policy learning is unstable. This is where better models and theories are needed.

Convergence Ideas: DIKWP's contribution to MAS is mainly in two aspects: clarifying the interaction semantic hierarchy and providing a collaborative framework.

Semantic Communication and Knowledge Sharing (D/I/K/P Layer): In MAS, agents need to communicate with each other (data layer interaction). If each agent communicates with raw data, the amount of communication is too large and the other party is difficult to understand. For example, when two unmanned vehicles interact, they directly send camera images to each other, and the other party's analysis cost is very high. DIKWP prompts that communication should take place at the information or knowledge layer: that is, the agent processes the local observation into semantic information/knowledge before sending it. For example, using natural language or symbols to express "there is an obstacle 100 meters ahead". This greatly reduces the communication load and allows the receiving agent to be directly integrated into its own knowledge graph. Therefore, when designing the agent communication protocol, semantic protocols (such as sharing environment models, intent signals) can be used instead of just sharing sensing data. This is already evident in swarms such as connected vehicles and drones: vehicles exchange positions and intentions without exchanging the original video. To achieve semantic communication, each agent needs to have a shared knowledge representation (the same information graph format or a unified intent dictionary). DIKWP provides a unified framework: as long as the internal state is represented in the DIKWP hierarchy, then it is natural to communicate with each other at the corresponding layer. For example, Agent A sends a local knowledge subgraph, and Agent B merges it into its own knowledge graph, that is, to achieve subjective and objective cognitive consistency. This sharing greatly reduces collaboration complexity because duplicate explorations are avoided. For example, if a robot learns that a certain path is not passable, it broadcasts knowledge, and there is no need to try anything else. One of the tricky issues with MAS is credit allocation (which agent contributes the reward), where knowledge sharing allows the group to work together to maintain a knowledge state of task progression, making it easy to calculate their contributions without having to learn blindly. The knowledge/intent layer of DIKWP can also be used to achieve distributed consensus: each agent shares its own intentions, and if there is a conflict, it reaches agreement through dialogue, or the upper layer coordinates the agent (acting as a scheduler, which may be a human or a central AI) for intent fusion. For example, multiple UAVs decide to assign area patrols, first report their own plans (P-layer communication), and then the scheduling algorithm optimizes according to the global knowledge, sends back the modified intention to them (knowledge layer + intent layer interaction), and finally acts in unison.

Division of Labor and Hierarchical Organization (W-Layer): MAS often requires division of labor to improve efficiency. DIKWP can be used to plan the organizational structure of the group: for example, which agents are responsible for perception (D/I layer), which are responsible for summarizing knowledge (K layer, equivalent to group memory), and which are responsible for final decision-making (W/P layer). This is similar to a human team, with scouts, staff officers, and commanders, each with its own duties. In the AI community, this level can be introduced: the low-level agent performs specific operations, and the high-level agent aggregates information to make policy decisions. In fact, this can naturally lead to distributed DIKWP: the entire MAS is a large system with different agents or sub-teams implementing functions at each layer. For example, in the UAV cluster disaster search, the peripheral UAVs quickly scan the area (data layer acquisition), the middle-level UAVs are integrated into an environmental map (knowledge layer generation), the UAVs are led to plan the overall search road (intelligent layer decision-making), and sub-tasks are assigned to each UAV (intent layer distribution). In this way, the complexity of the group is reduced, because the individual does not need to know and make decisions in the whole way, but only needs to do his or her own hierarchical tasks. The common master-slave architecture and hierarchical control are applications of this idea, except that DIKWP allows us to divide by semantic function rather than randomly. This helps with fault tolerance: if a knowledge fusion agent fails, the system knows that there is a problem with the knowledge layer, and can have a backup plan or be replaced by another agent, so that the whole line will not collapse. Another example is the blockchain network, which can be regarded as a MAS without a center, through distributed consensus to achieve knowledge unification (ledger), each node only needs to verify local transactions (information layer) and then broadcast to the network to wait for consensus to update the ledger (knowledge layer), decision-making actions (such as packing blocks) are done by specific nodes in turn (intelligence layer), and the general direction goal (maintaining security and consistency) is locked by the protocol (intent layer). Although it is not explicitly described in DIKWP, the process fits its layered spirit. This shows that DIKWP is universal, and can guide the design of hierarchical architectures, regardless of whether it is centralized or distributed.

Competitive Game and Complexity Reduction: In many MAS scenarios, there is a competitive relationship between agents, which will lead to a further increase in complexity, because each agent not only has to solve the complexity of the environment, but also predicts the opponent's strategy (policy nesting). DIKWP is also beneficial in gambling situations. For example, the adversary can be modeled at the knowledge layer by including it as a "part of the environment": the agent infers the opponent's intention (P-layer inference) based on historical actions and adds it to the knowledge as a known fact, and then uses this knowledge to find its own optimal strategy in the intelligence layer. This is similar to human strategic reasoning, assuming the opponent's goal before acting. With explicit intent inference and knowledge modeling, the adversary's uncertainty is reduced to a definite hypothesis, thus reducing computation. Traditional game solutions such as Nash equilibrium often need to consider all combinations of strategies (complexity explosion), but if the types of opponents' intentions can be greatly limited at the knowledge level, there are a lot of possibilities. For example, if the opponent is rational or pursues the greatest returns, this assumption itself is the limit of the opponent's intention, and then only the part of the opponent's strategy space needs to be considered. The reason why AlphaGo can beat people is that it implicitly learns that Go opponents are rational people who seek to win, and it estimates the distribution of opponents' strategies through neural networks, which is equivalent to reducing the branches of the game tree. This can be understood as an implicit knowledge-layer judgment and intent prediction.

Advantages: MAS adopts the DIKWP idea, which has multiple benefits: (1) Efficient communication: semantic information exchange replaces lengthy data synchronization, reducing network load and time delay. (2) Reliable collaboration: Sharing knowledge graphs and intentions allows all agents to know in their hearts, and it is not easy to go their own way, reducing friction and conflicts. Even conflicts can be identified and resolved as early as possible in the intent communication phase, rather than crashing in execution. (3) Scalability: With hierarchical organization, adding agents will not increase complexity linearly, because they can be grouped and summarized. For example, it is impossible for a team of 1000 people to communicate directly with everyone, and the complexity O(n^2) is too high, but after the hierarchical organization, it becomes an or level of communication efficiency. The same is true for machine swarms, which can be scaled up to thousands if there is a hub or hierarchy. (4) Learning and adaptation: The knowledge and experience accumulated by the group can be stored in the shared knowledge layer, and new agents can quickly query and learn without having to explore from scratch. Over time, the team got smarter. For example, a group of robots inspect factories and constantly summarize the knowledge of failure modes, so that no matter which robot encounters a similar signal, it can be warned in advance next time; This is better than the time and effort of each robot learning its own thing.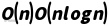

Implementation Challenges: Of course, multi-agent applications DIKWP need to solve the problem of standardized semantics: different agent architectures may be different, and allowing them to share knowledge and intent requires defining a unified format or protocol, which is a bit like multilingual machine translation, which requires sharing ontologies and languages. It is especially difficult when heterogeneous agents collaborate. However, there are studies doing this, such as the "Agent Communication Language ACL", which is an attempt to standardize intent communication. At present, there is no broad general standard, but DIKWP provides a candidate general ontology: all agents should at least agree on the division of concepts such as data, information, knowledge, intelligence, and intention, and then use a common format at each layer (e.g., the knowledge layer uses some kind of logical statement, and the intent layer uses some kind of task description language). If this standard can be implemented, the collaboration between agents will be greatly simplified. In addition, hierarchical organization is at risk: it can introduce a single point of failure and delays. However, redundancy and partial decentralization can be used to alleviate it, such as multiple agents responsible for redundancy and knowledge fusion, or intent negotiation using decentralized algorithms.

In conclusion, the integration of DIKWP and MAS paints a prospect: both human-machine and machine-machine hybrid systems can form intelligent groups rather than chaotic gangs through good docking at the semantic level. Each agent operates in an orderly manner according to DIKWP, and communicates smoothly with each other through the DIKWP hierarchical protocol. Such clusters show far more strength than individuals in the face of complex tasks, and because the complexity is reasonably distributed between the individual and the collective, the system can scale to a very large scale and still remain efficient. This is similar to the pattern of social organisms in nature (ant colony, bee colony, human society), which can be described as the direction of artificial swarm intelligence. DIKWP acts as a "ubiquitous translation layer" and a "structural blueprint" to guide us on how to organize local intelligence into overall intelligence.

Multidisciplinary Links: Cognitive Science, Complexity Theory and Computational Neuroscience

As a framework for complexity analysis and cognitive modeling, the origins and influence of the DIKWP model go far beyond computer science itself. It is naturally related and complementary to cognitive science, complex systems theory, computational neuroscience, and other fields. Through a multidisciplinary perspective, we can understand the significance of the DIKWP model more comprehensively, and examine it in a broader scientific context to further validate and enrich its connotation.

Cognitive Science and Psychology Perspectives

The hierarchical structure of DIKWP can correspond to the classical model of human cognitive processes to a considerable extent. In cognitive psychology, human information processing is often described as the process of feeling (perception) - perception (understanding) - memory (knowledge) - decision-making, which corresponds to the D→I→K→W→P level of DIKWP:

Sensory/perceptual versus data/information layer: The human sensory organs obtain environmental stimuli, which is equivalent to the data layer input; Through the mechanism of attention and perception, a subjective representation of objective things is formed (such as recognizing that what is seen is a chair), and the corresponding information layer gives meaning to the data.

Memory/Knowledge Layer: Perceived information is matched or stored in a memory bank, including episodic memory, semantic memory, etc. This is the knowledge layer: the brain stores a large network of knowledge about the world, and when new information comes in, it is integrated and associated with existing knowledge (e.g., when you see a chair, you think "you can sit", "this is furniture").

Reasoning vs. Intelligence: Before making an action, people think and reason based on knowledge and current information, and plan ways to achieve their goals. In psychology, decision-making and problem-solving processes correspond to the intelligence layer. Many studies have shown that humans construct psychological problem spaces to search for solutions, similar to search planning in AI.

Intention/Motivation vs. Intention Layer: Psychology emphasizes the driving role of motivation and purpose in behavior, such as Maslow's hierarchy of needs, Deci and Ryan's self-determinism, all of which discuss the goal orientation of human behavior. This corresponds exactly to the intention layer of the DIKWP: it determines the ultimate purpose and criterion of the cognitive system (person). With intention, people will selectively perceive, retrieve relevant knowledge and make targeted decisions, and when there is no purpose, it is easy to distract aimlessly.

Therefore, DIKWP can be seen as an abstraction of the human cognitive architecture. This means that we can draw on a wealth of cognitive science experiments and theories to support the DIKWP model. For example:

Working memory vs information layer capacity: In psychology, there are Miller's "7±2" rule, which states that people can only process a limited amount of information at a time, which is similar to the limited complexity of the information layer. The information layer of DIKWP may also have a similar "bandwidth", which needs to be considered when designing the AI, otherwise the system will be overloaded or omit information (e.g. UI design to avoid presenting too much data to the user/AI at once).

Knowledge Representation and Organization: Cognitive science studies how knowledge is represented in the human brain (e.g., semantic networks, archetypal theory). The DIKWP knowledge layer can draw directly from these models. For example, the semantic network model can be used as the infrastructure of the DIKWP knowledge graph; The archetypal theory of concept classification reminds us that when the knowledge layer deals with complexity, it is possible to reduce the matching cost through hierarchical classification (it is easier for people to distinguish typical examples, but it is difficult for edge examples).

Metacognition: Humans have the ability to monitor and regulate their own cognitive processes, such as looking up when they realize that they don't understand something. This is equivalent to a higher-order intention (learning X) to direct lower-level behavior. DIKWP can be extended to introduce a metacognitive layer, but it can also be seen as a feedback moderation function of the intent layer. AI is designed to have a mechanism to monitor the state of each layer, such as the attention model to monitor the information layer, and the strategy evaluation module to monitor the results of the intelligence layer, which is consistent with the concept of executive control in cognitive science.

Cognitive Development and Learning: Piaget proposed in psychology that the stages of children's cognitive development: perceptual-motor stage, pre-operation, concrete operation, and formal operation, which correspond to the gradual strengthening of the acquisition of data, the formation of knowledge, logical reasoning, and abstract planning. The DIKWP model may also reflect a similar development path in machine learning systems: first learn to perceive, then gradually learn to reason, and finally abstract the plan, as if the AI has gone through "childhood". This suggests that we can train AI in an orderly manner by cognitive stage, similar to the phased training of Transformer described above.

Complex Systems Theory Perspectives

Complex systems theory studies complexity emergence and dynamics across domains, such as network science, chaos theory, fractals, adaptive systems, etc. The DIKWP model treats intelligent systems as multi-level complex systems, which coincide with many complexity concepts:

Emergence and hierarchy: Complex systems often have new properties (emergence) at higher levels that are not present at lower levels. The intelligent decision-making of the DIKWP intelligent layer is the interaction of data, information and knowledge. Just as the ant colony is simple individually, but the wisdom of the crowd emerges. DIKWP provides a framework to dissect this emergence: to describe the overall complexity through an interlayer coupling mathematical model. Tononi Integrated Information Theory (mentioned Φ) is also a tool for measuring emergences in complex systems, which can be linked to the total complexity of the DIKWP.

Network topology and complexity: Complex network theory has studied the influence of network structure on diffusion and coordination. For example, small-world network connections reduce the path length, accelerate information dissemination, and reduce the complexity of group thinking. The DIKWP knowledge layer often exists in the form of a network (knowledge graph), and its topology has an impact on the inference complexity: a loose and disordered network may need to search for many nodes (high C_K), while a small world structure with clusters and long-range connections allows relevant knowledge to arrive faster. Therefore, it makes sense to use complex network metrics (clustering coefficient, average distance) to evaluate knowledge graphs, and perhaps find ways to reduce the complexity of knowledge retrieval, such as optimizing the knowledge base structure to make the required knowledge closer to each other (similar to cache locality).

Adaptation and Evolution: Complex systems often reduce entropy and increase order through evolutionary adaptation. The knowledge graph and strategy of the DIKWP system are evolving in continuous learning. Evolutionary algorithms or ecological theories can be used to simulate the evolution of the DIKWP layer, such as the knowledge layer continuously "evolving" to produce more concise and efficient representations (compressing effective complexity), and the intelligent layer strategy evolving adversarial strategies in interaction. Treating AI as a complex adaptive system can introduce ideas such as genetic algorithm optimization for multiple objectives and immune system theory to enhance robustness.

Steady-state and phase transition: Complex systems can have different phases under different parameters: for example, each subsystem is independent at low coupling, and the overall synergy increases suddenly at high coupling. By analogy with AI, is there a "phase transition point" – for example, when knowledge accumulates to a certain level, the expression of intelligence suddenly changes from chaos to order (some kind of "intelligence tipping point"). This can be done using complexity theories such as criticality detection. In the DIKWP model, the critical value of some coupling parameters may induce intelligent phase transitions, such as the system comprehension ability is sharply enhanced when the connectivity of the knowledge graph exceeds a certain threshold. Multidisciplinary research in this area may reveal the quantitative conditions for the emergence of intelligence, which can help us design more effective learning paths to cross the threshold.

Herbert Simon's hierarchical almost decomposition theory has been cited above. In addition, Ashby's Law (Complexity Matching): The control system must be complex enough to cope with the complexity of the environment. In DIKWP, this means that the knowledge/strategy complexity of the AI must match the complexity of the environment, otherwise it cannot be fully processed. In complexity theory language, AI needs to have enough "entropy capacity" to capture external entropy. To this end, DIKWP reminds to increase the model hierarchy and structure to expand the capacity.

Computational Neuroscience with Brain-Inspired Perspectives

Computational neuroscience is dedicated to describing brain function with mathematical models, and there are frameworks such as neural information encoding, neural network dynamics, etc. The DIKWP model can be cross-corroborated with a number of brain science perspectives:

Brain Partitioning and Global Workspace: Global workspace theory (Baars, Dehaene, etc.) proposes that the brain has a global workspace that integrates information from various modules to generate consciousness. This is similar to the intelligence/intention layer of DIKWP that integrates information from sensation and memory for decision-making awareness. DIKWP emphasizes bidirectional interpretability and semantic mapping, which corresponds to prefrontal-sensory feedback in the brain: high-level intention (prefrontal) mediates lower-level perceptual (visual cortex) processing through attentional mechanisms. For example, when there is a purpose, focus on the relevant information of the goal. In our discussion of the complexity of the DIKWP coupling, we also pointed out that high-level (P-layer) guidance can reduce the complexity of low-level data processing, which is consistent with the top-down attention to reduce the perceived load found by neuroscience.

Brainwaves and hierarchical rhythms: Brainwaves in different frequency bands of the brain are guessed to correspond to different levels of information processing, such as local processing of γ waves and global coordination of theta waves. DIKWP hierarchical interactions may have similar rhythmic coordination: the lower level is fast looping, and the upper level is slow to regulate. Understanding this can optimize AI asynchronous architectures, such as high-frequency refresh for low-level sensing and low-frequency update for high-level decision-making, to mimic the brain-level rhythm and reduce unnecessary computational synchronization.

Brain energy consumption and complexity: The brain consumes about 20W of energy and does super complex calculations thanks to its parallel distributed and predictive mechanisms. DIKWP provides a similar division of labor and reduces double computation through knowledge and prediction (e.g., semantic elasticity prevents repeated processing of variants, as in the same way that the brain "automates familiar patterns"). We can learn from the theory of predictive coding: the brain constantly predicts sensory input, processing only error signals. Applied to DIKWP, the AI information layer does not process the parts that can be predicted by the knowledge layer, and only focuses on new information (reducing complexity). Computational neuroscience models have shown that this explains perceptual feedback loops.

Neuroplasticity and Learning: The brain strengthens knowledge by changing connections through plasticity, which corresponds to the evolution of the DIKWP knowledge graph. Neuroscience has pointed out that oversimplification leads to cognitive rigidity, and over-complexity leads to lack of energy, and there is an optimal state of complexity. The same is true for AI, where the knowledge network should not be overly sparse or dense, and should balance generalization and memory. This can be achieved in training through complexity constraints such as Kolmogorov complexity regulars, which keep the model brain-like at a moderate level of complexity.

Another connection is the similarities and differences between deep learning and the brain. The current deep network lacks explicit symbolic manipulation and planning, which is exactly what the DIKWP model is trying to introduce, and the brain seems to have both, both (with continuous neural computation and discrete logical reasoning). Therefore, DIKWP+ deep learning = one step closer to "whole-brain AI". Neuroscience provides a lot of evidence that the brain is partitioned module + global coordination, and multimodal integration is also the division of the brain to distinguish modalities and then merge. This gives DIKWP bioplausibility support.

Finally, it is worth mentioning that in the field of consciousness science, the DIKWP model confronts artificial consciousness systems. Some theories (e.g., IIT) attempt to quantify the complexity of consciousness, and the DIKWP model may provide a framework for the construction of artificial consciousness, and use the IIT φ to verify the overall comprehensiveness of the interaction between the layers. When the DIKWP Layer 5 interconnection is tight, the φ may be higher, and the system may be more "self-contained". Of course, this is speculation, but interdisciplinary attempts may lead to breakthroughs.

The significance of the convergence of disciplines

Through multidisciplinary linkage, we not only validate the rationality of the DIKWP model (because it has corresponding concepts in different fields), but also enrich its toolbox and goals. Cognitive science inspires AI to work more humanly, complex systems theory provides mathematical tools for analytic hierarchy emergence, and neuroscience inspires engineering to implement details such as asynchronous parallelism and prediction mechanisms.

In turn, the successful application of DIKWP will also feed back into these fields: for example, in cognitive science, AI has implemented a DIKWP artificial consciousness model, which can be used to explain the operation of human consciousness by analogy; In complexity science, a controllable artificial complex system can help test complexity theory hypotheses. In neuroscience, a certain layer of parameters or behaviors of an AI system may be able to correspond to brain imaging observations to help understand brain coding.

In summary, the DIKWP model is naturally an interdisciplinary product: it applies the methodology of computer science (hierarchical modularity) to psychological cognitive problems, and extends complexity analysis to the field of semantics. In the future, if we want to build truly powerful and reliable artificial intelligence, we must rely on this kind of cross-border integration. From a biomimicry perspective, we can reproduce some of the mechanisms of biological intelligence (e.g., stratification, knowledge sharing, goal orientation) in artificial systems to achieve similar dexterity and efficiency. From an engineering perspective, multidisciplinary algorithms and theories can help us break through current AI bottlenecks (e.g., explainability, instability), and DIKWP is a framework that incorporates the essence of this.

Therefore, it is necessary to maintain multidisciplinary cooperation in promoting the research and application of the DIKWP model: discussing artificial consciousness assessment with cognitive scientists, comparing brain activity patterns with neuroscientists, and studying self-organization and chaotic edges with cybernetics and complexity theorists. This will ensure that the DIKWP methodology continues to evolve closer to the universal principles of intelligent systems, and that all disciplines can draw new inspiration from it.

conclusion

By expanding and deepening the "System Complexity Analysis Methodology Based on DIKWP Model", this paper constructs a comprehensive analysis system with rigorous structure, rigorous logic and cutting-edge value. We comprehensively demonstrate the advantages of the DIKWP five-layer model in the modeling of cognitive intelligent systems: it provides powerful capabilities for hierarchical representation and semantic characterization of complex systems, allowing us to capture semantic complexity and intent drivers that cannot be covered by traditional complexity analysis. We enrich the definition and connotation of each layer (data, information, knowledge, wisdom, and intention), derive the quantitative formulas of their respective complexity, and explain in detail based on theoretical sources and practical metrics: from layer D to linearly increase with data scale, layer I is constrained by feature extraction function, layer K depends on knowledge retrieval and matching performance, layer W is related to state space and the number of policy generation, and layer P is measured by target switching frequency and feedback loop length. These derivations are not only supported by classical algorithm complexity theory, but also integrated into the perspectives of semantics and cognitive theory, so that the complexity analysis is closer to the actual working mechanism of intelligent systems.

When examining the interaction and coupling between layers, we systematically analyze how multi-layer coupling leads to the emergence and evolution of overall complexity, and establish a mathematical model to describe this evolution process. We point out that the positive or negative coupling term between layers can deviate the overall complexity from the sum of the independent contributions of each layer, which explains the nonlinear increase or decrease of complexity in intelligent systems. By introducing discussions of semantic complementarity, feedback loops, and evolutionary dynamics, we paint a picture of complexity over time and experience: agents learn and adapt to shift parts of complexity from online to offline, from high-level to low-level, or vice versa, keeping overall complexity manageable. This understanding of the "flow" of complexity makes sense for designing scalable AI systems. We also emphasize the modulating effect of high-level intent on low-level processing and the constraining effect of knowledge on decision search—both of which help to avoid the explosion of combinatorial complexity and are quantified in our model.

Through the in-depth analysis of three new case scenarios (AI education system, autonomous unmanned system, and multi-modal large model platform), we verify the universality of the DIKWP model for different types of intelligent systems, and show how to apply the framework to diagnose complexity bottlenecks and formulate optimization strategies. In the AI education system, we have seen a clear correspondence to the complexity of each layer of DIKWP: the collection of massive student data, the extraction of student status information, the retrieval and utilization of the teaching knowledge base, the planning and selection of teaching strategies, and the setting and switching of teaching goals, each link can be optimized under the DIKWP level, so as to achieve efficient and credible personalized teaching. In autonomous unmanned systems, the arduous processing of sensor data and the complexity of real-time decision-making have been deconstructed in layers, and we propose that by strengthening the information layer perception algorithm and the utilization of knowledge layer maps, combined with hierarchical planning, the complexity and pressure of unmanned vehicle decision-making can be effectively reduced, and the safety and reliability can be improved. In the multimodal large model platform, despite the huge system, we can still divide the process of input multimodal data processing (layer I), the application of implicit knowledge of model parameters (layer K) and the final language generation decision (layer W), and find that the problems of illusion and instability of the current large model can be alleviated by introducing external knowledge and explicit control intentions. These cases fully demonstrate that the DIKWP model can be used as a unified methodological framework to guide system design, complexity evaluation, and performance improvement across different application fields.

The cutting-edge concepts we introduce such as semantic elasticity, relative complexity of subjects, and semantic space flow further expand the dimension of complexity analysis and provide tools for quantifying the ability of semantic level. The quantitative framework of these concepts allows us to assess the extent to which a system is flexible in understanding diverse inputs, how its complexity depends on the subject's knowledge background, and how much information is lost in cross-layer and cross-subject semantic transfers. By incorporating these elements into the complexity model, we are able to "see" previously hidden sources of complexity in our analysis (e.g., additional interaction costs due to semantic incompatibility) and make more refined optimizations. For example, improving semantic elasticity can be seen as effectively reducing the input size N, because the system treats many equivalent variants as a class; Another example is the relative complexity of the subject that reminds us of the importance of training and experience accumulation – through the expansion of knowledge, the actual perceived complexity of the system decreases. These insights are forward-looking and point to a future in which AI systems will need to be evaluated by reporting not only on algorithmic complexity, but also on semantic complexity metrics to fully characterize system performance.

The integration of the DIKWP model with the current mainstream AI framework shows that this methodology is not separated from popular technologies, but on the contrary, it can be used as a high-level idea to infiltrate various concrete implementations and give them new vitality. We discuss the integration with the Transformer large model, and point out that the black box large model can become more transparent and controllable by explicitly implanting the knowledge retrieval module and intention control mechanism in the Transformer structure, and the existing retrieval enhanced language model and multi-step inference strategy have confirmed the feasibility of this direction. We explore the integration with reinforcement learning and find that DIKWP can help reinforcement learning to achieve state representation refinement, hierarchical policy decomposition and knowledge transfer, thereby greatly improving sample efficiency and generalization ability, which is similar to the human learning process and is consistent with the current trend of hierarchical reinforcement learning. In terms of multi-agent systems, the DIKWP framework is almost naturally suitable for designing multi-agent communication protocols and collaboration architectures: through unified semantic level communication, each agent can efficiently share information and coordinate intentions, and the complexity is no longer exponentially exploding, but is well controlled. These discussions of convergence indicate that the future intelligent system is likely to be multi-paradigm fusion, with both the perception ability of deep learning, the reasoning ability of symbolic knowledge, and the organization ability of distributed collaboration. The DIKWP model provides a compendium to accommodate these paradigms and help them complement each other.

The multidisciplinary link increases our confidence and depth of understanding of the DIKWP model. In cognitive science, DIKWP is highly compatible with human cognitive architecture, from which we draw on a large number of experimental facts (e.g., working memory capacity, hierarchical decision-making strategies) to corroborate the details of the model, and we also see that the analysis of artificial systems can in turn provide new quantitative tools for cognitive science (e.g., using the DIKWP complexity framework to measure human perception of task difficulty). Complex systems theory gives us mathematical and conceptual tools to deal with the emergence of the overall complexity of the system, and Tononi's integrated information theory and Simon's near-decomposition principle directly or indirectly support the hierarchical validity and interaction importance of the DIKWP model. Computational neuroscience and brain science provide us with a vivid and empirical source of inspiration: brain partitioning, attention mechanisms, hierarchical rhythms, etc., correspond to the DIKWP hierarchy, and we draw biomimetic inspirations from them to optimize artificial systems, such as introducing predictive coding to reduce redundant computation, using asynchronous parallelism to improve efficiency, etc. These interdisciplinary connections not only enrich the theory, but also bring the DIKWP model to the forefront of interdisciplinary discussions, enhancing its academic value and persuasiveness.

In conclusion, through the extended DIKWP model methodology in this paper, we preliminarily construct an academic framework that integrates semantic hierarchy and complexity analysis. This framework can provide more granular insight into the internal mechanisms and bottlenecks of cognitive intelligence systems, and provide new ideas and tools for the design, optimization and evaluation of complex systems. It not only inherits the RG of classical complexity theory, but also absorbs the insight of cognitive semantics, which can be described as both soft and hard, and bridges the gap between pure computational analysis and pure cognitive analysis. For academic research, it establishes a structured blueprint for exploring the realization of artificial consciousness and the evaluation of universal intelligence. For engineering applications, it points out a specific path to reduce complexity and improve performance for building large-scale AI systems and swarm intelligence platforms. With the exponential expansion of the scale and functionality of AI systems, the old analysis paradigm has been stretched thin, and the proposal and improvement of the DIKWP model methodology meet this demand at the right time. Looking forward to the future, we will further improve the system: calibrate the complexity model of each layer through more empirical studies, analyze the nonlinear coupling between layers through theoretical research, and verify the multidisciplinary fusion effect through practical application. We believe that the hierarchical holographic semantic complexity analysis represented by the DIKWP model will become one of the important pillars of the new generation of artificial intelligence theory, and lay a solid theoretical foundation and methodological guidance for the realization of explainable, reliable and powerful intelligent systems.

人工意识与人类意识

人工意识日记

玩透DeepSeek：认知解构+技术解析+实践落地

人工意识概论：以DIKWP模型剖析智能差异，借“BUG”理论揭示意识局限

人工智能通识 2025新版 段玉聪 朱绵茂 编著 党建读物出版社

主动医学概论 初级版

世界人工意识大会主席 | 段玉聪

邮箱|duanyucong@hotmail.com

世界人工意识科学院

邮箱 | contact@waac.ac