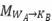A Study on the Limit Structure and Evolution Mechanism of

A Study on the Limit Structure and Evolution Mechanism of Cognition and Innovation in theDIKWP × DIKWP Semantic Interaction Space

Yucong Duan

International Standardization Committee of Networked DIKWPfor Artificial Intelligence Evaluation(DIKWP-SC)

World Artificial Consciousness CIC(WAC)

World Conference on Artificial Consciousness(WCAC)

(Email: duanyucong@hotmail.com)

Introduction

The Data-Information-Knowledge-Wisdom-Purpose (DIKWP) model is an extension and reconstruction of the traditional DIKW (pyramid) model. It introduces the "Purpose" layer into the cognitive process framework to emphasize the consistency between action decisions and final goals. Unlike the linearly layered DIKW model, the DIKWP model connects five cognitive levels (Data D, Information I, Knowledge K, Wisdom W, and Purpose P) through a networked, bidirectional connection, forming a closed, multi-directional feedback space. This "mesh" structure allows for interaction and semantic propagation between any layers, thus more realistically simulating the cyclic feedback characteristics of complex cognitive systems.

The DIKWP × DIKWP semantic interaction space refers to a Cartesian product-style interaction model between two DIKWP five-layer structures. In short, we consider two cognitive entities or states, each with a DIKWP five-layer architecture. All possible layer-to-layer mappings between them constitute a 25-dimensional (5×5) semantic interaction space. In this space, any layer of one cognitive system (e.g., the Data layer D) can exchange and feedback semantic information with any layer of another system (e.g., the Knowledge layer K). By constructing the DIKWP × DIKWP model, we can formally describe how two cognitive subjects (or the same subject at different time states) conduct complex semantic communication and co-evolution through various levels. Such a model provides a formal mathematical foundation for us to study the limit structure and evolution mechanism of cognition and innovation in a closed semantic system.

This report aims to systematically derive and discuss the limit structure and evolution mechanism of cognition and innovation in the DIKWP × DIKWP interaction space, based on the DIKWP semantic mathematics system. We will not rely on existing models from traditional cognitive science or innovation economics but will construct a completely independent theoretical system to analyze the following issues:

1.Reconstruction of the DIKWP × DIKWP Model: Define the tensor mapping relationships between the five layers (D, I, K, W, P) in the cognitive interaction structure, as well as the mechanism of semantic propagation between layers.

2.Derivation of the Closedness of Semantic Space: Prove whether the DIKWP × DIKWP interaction model constitutes a semantically self-consistent and closed cognitive system, and analyze the boundary constraints that this closedness may impose on innovation generation.

3.Tensor Transition Expression of Innovation: View "innovation" as a mutation phenomenon in the DIKWP tensor dimension, explore its mechanism triggered by the superposition of semantic differences or the compression of heterogeneous semantics, and express this transition in tensor form.

4.Limit Analysis: Discuss the expressive limits and capability boundaries of the DIKWP semantic space, including:

oExtreme cases of tensor expression (e.g., incompatible tensors between W-P layers, non-generatable semantic blocks).

oBoundaries of expressive power (e.g., maximum cross-layer alignment range, maximum semantic inversion width).

oUnpredictable structures that appear during the DIK→W transformation process.

5.Conception of Hyper-DIKWP Logic: Explore how to "transcend" the limitations of the existing DIKWP structure, proposing concepts such as jumping out of the DIKWP space, constructing a non-linear Purpose (P) space, and "anti-W" transition paths, to envision new logical forms beyond the current framework.

6.Evolutionary Closed Loop of the DIKWP Cognitive Economy: Treat the DIKWP semantic space as a "cognitive economy" system, discussing how individuals or artificial intelligence (AI) can maximize the utility of innovation tensors through strategic design in a closed semantic space, forming a self-evolving closed-loop process.

The entire report adopts a rigorous academic style and a clear logical structure, progressively deriving the contents of each part. We will first reconstruct the mathematical definition of the DIKWP × DIKWP model, then proceed with the analysis of semantic closedness, the interpretation of innovation mechanisms, the discussion of limit conditions, followed by proposing possible hyper-structure concepts, and finally discussing the strategic closed loop for optimizing innovation within the closed space. All derivations are based on the consistent logic within the DIKWP semantic system, without relying on external empirical theories, thereby ensuring the independence, autonomy, and self-consistency of this theoretical system.

1. Reconstruction of the DIKWP × DIKWP Model

In this section, we formally reconstruct the DIKWP × DIKWP cognitive interaction model, clarifying the tensor mapping relationships between the five-layer structures and explaining the mechanism of semantic propagation.

1.1 Definition of the Five-Layer Structure

The DIKWP five-layer structure includes the following levels:

·Data Layer (D): Contains raw, unprocessed inputs, such as signals collected by sensors, observed facts, and recorded discrete values. Semantically, the data layer carries the lowest level of semantic units, characterized by fine granularity and semantic isolation, not yet forming contextual meaning.

·Information Layer (I): A collection of information formed after data is processed, organized, and formatted. The information layer endows raw data with a certain structure or interpretation, giving it understandable patterns or meanings. For example, organizing scattered data points into a report or recognizing objects in an image are processes of converting data into information. The semantic units of the information layer have preliminary contextual associations and meanings.

·Knowledge Layer (K): Generalized knowledge, concepts, or laws formed by the fusion, induction, or learning of a large amount of information. The knowledge layer contains the understanding and association of information, integrating information from different sources to form a semantic structure with a higher level of abstraction (such as theorems, models, rules, conceptual systems). The content of the knowledge layer can guide the interpretation of future information and has a certain universality.

·Wisdom Layer (W): The level of making wise decisions or insights based on knowledge, combined with experience, judgment, and values. The wisdom layer represents a profound understanding and good use of knowledge, involving comprehensive consideration and judgment of complex situations. The semantic content of the W layer often manifests as principled insights, strategic choices, or a global perspective on complex issues.

·Purpose Layer (P): Represents the fundamental motivation, goal, or intention behind the actions of a cognitive subject. The purpose layer provides direction and evaluation criteria for the entire cognitive process—the collection of data, processing of information, acquisition of knowledge, and application of wisdom should all be consistent with the established purpose. The semantic unit of the P layer is a description of "why to do it" and "what is desired to be achieved," which can be a clear goal requirement or an implicit value orientation.

The five layers together constitute a complete semantic spectrum from concrete to abstract, and then to purpose-oriented, within a cognitive system. The traditional DIKW model presents a pyramid-like, bottom-up, unidirectional accumulation. In the DIKWP model, due to the introduction of the Purpose (P) layer and the allowance for feedback, the five layers are actually a highly interconnected, cyclically acting mesh system. That is, in addition to the general D→I→K→W (from data to wisdom) bottom-up inference process, there is also top-down guidance (e.g., W→K→I→D, where wisdom and purpose guide data collection and information processing in reverse), as well as horizontal interactions between layers (e.g., mutual reference between the knowledge and information layers, connections between different knowledge points at the same layer). This multi-directional connection can be formally described by tensor mapping.

1.2 Tensor Mapping Model

Tensor mapping refers to the use of multi-dimensional mappings or matrix forms to describe the interactions between the DIKWP levels. In the DIKWP × DIKWP model, we consider two cognitive entities or states: denoted as System A and System B, each with its own D, I, K, W, P five-layer structure. We view the interaction between the layers of the two systems as a mapping from a certain layer of System A to a certain layer of System B, which can be generally abstracted as a five-dimensional to five-dimensional mapping space.

Formally, we define:

·

·

The DIKWP × DIKWP interaction space can be represented as the set of mappings on the Cartesian product . For any  and , we use  to denote a process or "conversion module" for semantic mapping from layer X of system A to layer Y of system B. Since , there are a total of  possible mapping modules, forming a  mapping matrix or a second-order tensor. The elements of this tensor correspond to specific layer-to-layer conversion mechanisms.

Mapping Matrix Representation: For clarity, we can construct the following mapping matrix, where rows represent the source layer (System A) and columns represent the target layer (System B), with each cell corresponding to a semantic transformation:

A→B

In these 25 mappings, each corresponds to a specific semantic interaction channel. For example:

·data of System A becomes the information of System B through some filtering or interpretation mechanism. This corresponds to A outputting raw data, which B parses to form meaningful information.

·purpose of System A guides the data collection or representation method of System B. For example, the goal directive of A (which could be a user or a higher-level system) determines which raw data B needs to acquire.

·knowledge of System A is directly transferred to or absorbed by B as B's knowledge, such as two subjects directly sharing knowledge base entries.

·wisdom (decision/insight) of System A triggers an adjustment in the purpose of System B. For instance, a mentor's wise insight influences a student to reset their research goals.

The diagonal of the matrix (e.g., , ) represents same-layer alignment interactions: the two systems exchange or align corresponding content at the same level, such as data-to-data transfer (sensor networks sharing raw data) or knowledge-to-knowledge exchange (academic exchanges sharing knowledge). The off-diagonal elements represent cross-layer mappings, including "bottom-up" cross-layer (e.g., , where A's data is directly sublimated into B's knowledge) and "top-down" cross-layer (e.g., , where A's wisdom directly guides B to produce certain information), as well as various other influences between heterogeneous layers (e.g., , where A's information affects B's purpose setting).

It is worth noting that the DIKWP × DIKWP model is not limited to the interaction of two different subjects. The evolution of the same cognitive subject at different times can also be described similarly: here,  represents the state of each layer of the system at time ,  represents the state of each layer at time , and  describes the evolution process from layer X at time  to layer Y at time . In this view, the 25 mappings depict how the various layers of a single cognitive system transition and connect within one cognitive cycle, completing the transition from an initial cognitive state to the next.

1.3 Semantic Propagation Mechanism

With the formal description of tensor mapping above, we next define the semantic propagation mechanism, i.e., how semantic content flows, transforms, and maintains self-consistency within the DIKWP × DIKWP network.

Semantic Units and Representation: Let there be a semantic unit  at a certain layer X (which can be  or ), representing a piece of content at that layer. For example,  might be a set of raw sensor readings, and  might be a law or concept in System B. If there is a mapping module  connecting layer X to layer Y, then  will produce an output semantic unit  at layer Y. This output  is integrated with the original content of layer Y to form a new semantic state for layer Y.

Propagation that Maintains Semantic Consistency: For the self-consistency of semantic propagation, we require each mapping  to maintain semantic consistency and interpretability during transformation. That is, the semantics of the output  at layer Y should be derivable from the semantics of the input  at layer X through the defined transformation rules of M, and it should be understandable to system Y. The same mapping should produce the same semantic output for repeated identical inputs (determinism) and produce outputs corresponding to the input for different inputs (plasticity). For example:

·

·

Bidirectional Feedback and Closed Loop: Since a feature of the DIKWP model is the introduction of purpose to form a closed feedback loop, the DIKWP × DIKWP interaction is also usually bidirectional. Systems A and B can be each other's environment and information source; information can flow from A to B and also from B to A, forming a loop. For instance, while  is transmitting, there might be a feedback  (System B's wisdom influences System A's data needs or collection). This means that in a complete interaction process, we might experience a series of mapping sequences: , going back and forth between multiple levels until some equilibrium is reached or a specific task goal is completed.

Through the above mechanism, semantic content propagates within the DIKWP × DIKWP space: it is generated at one layer of a system, reaches a layer of another system via mapping, causing a change in the semantic state of that layer; then, the affected system provides feedback through internal or external mappings. The whole process is like a flow in a multi-level, multi-dimensional semantic network. Formally, we can view a series of concatenated mappings as a composition or convolution of tensors. For example:

and so on. Semantics propagate through the composite effect of mappings between different layers, but the composition of these mappings does not jump outside the set of layers defined by DIKWP, which lays the groundwork for discussing the closedness of the semantic space in the next section.

It needs to be emphasized that the reconstruction of the DIKWP × DIKWP model provides a highly flexible framework for semantic interaction. Within this framework, the traditional unidirectional cognitive process is expanded into a fully interconnected network: it covers not only vertical hierarchical progression (the elevation from data to wisdom, and then to purpose) but also includes horizontal cross-layer interactions (direct transformations between any layers), while allowing for circular feedback loops (regulating preceding processes through purpose). Such a model provides us with sufficient freedom and formal rigor to analyze the limit behaviors and innovation mechanisms of cognitive systems.

2. Derivation of the Closedness of Semantic Space

After establishing the DIKWP × DIKWP model, we need to examine the closedness of this semantic interaction space. The closedness of a semantic space refers to whether any semantic operation or derivation conducted within this model always remains confined within the five semantic layers defined by DIKWP, without generating new semantic categories that exceed this system. We must also verify whether, under the closed-loop multi-layer interaction, the semantic evolution of the system remains self-consistent without logical contradictions. In other words, we aim to prove whether the DIKWP × DIKWP model constitutes a semantically consistent and closed cognitive system, and based on this, analyze the boundary constraints this closedness imposes on innovation.

2.1 Definition of Closedness

Formally, let  represent the DIKWP × DIKWP semantic space, which includes all combinations of the five-layer semantic states and the inter-layer mapping rules. If for any semantic element within  and any operation defined within , the result of the operation still belongs to , then  is said to be closed under that operation. In our context:

·Semantic elements refer to semantic units belonging to a certain layer (D/I/K/W/P) or their collections and combinations.

·Operations refer to the transformation, inference, or generation of new semantic content on these semantic elements through DIKWP mappings (including single-step mappings and multi-step composite mappings).

Closedness requires: for any initial semantic content belonging to a certain layer, after applying any series of DIKWP inter-layer mappings, the resulting outcome can still be identified as semantic content belonging to one of the five DIKWP layers. It should not produce a new type of semantics that cannot be characterized by any concept in D/I/K/W/P. At the same time, during this process, the system does not need to reference new rules or elements from outside the system; all evolution originates from the existing structures and rules within the system.

Consistency requires that no logical contradictions arise during internal evolution, meaning the deduction of semantic content follows consistent rules and does not lead to self-contradictory situations after cyclic feedback. For example, the system will not simultaneously generate "proposition A is true" and "proposition A is false" as irreconcilable knowledge; the purpose layer will not simultaneously have two mutually exclusive ultimate goals without further rules to resolve them.

In short, we hope to prove:

·Closed: , the mapping sequence  (where each  is some , with , and the composition of the mapping sequence means multiple transformations according to the semantic propagation mechanism described earlier).

·Consistent: For a set of semantic states  in , if  satisfies a set of semantic constraints (e.g., consistency, axiomatic system), the new set  obtained after evolution through a mapping sequence still satisfies these constraints, or the system has internal mechanisms to resolve potential conflicts, thereby maintaining overall consistency.

2.2 Proof of Closedness

(1) Closedness: The DIKWP system covers five semantic categories from concrete facts to abstract goals, which already comprehensively covers the types of elements in general cognitive processes. Our mapping rules all use these categories as starting and ending points, without introducing a sixth external category. Therefore, it can be expected that the DIKWP × DIKWP space is closed in terms of semantic categories. Let's detail this point:

·Basic Closure: Take a most basic mapping . Its input  belongs to a known layer X. According to the mapping definition, the output  should belong to the semantic range of layer Y. If 

oThe output of  must be information; otherwise, it is not an "information layer mapping."

oWhat  provides should be some kind of wise decision or insight; otherwise, the W layer cannot use it directly.

Therefore, the result of any single-step mapping still falls within one of the DIKWP layers.

·Composite Closure: Any composite mapping sequence  can be viewed as a chain process where the output of one mapping becomes the input of the next. Assume the initial input  belongs to layer . After the first mapping , we get any finite-step composite mapping will not produce a "sixth type of semantics outside the five layers."

In summary, based on the idea of mathematical induction: single-step mapping closure holds; if the result after k steps is still within the system, then the result after k+1 steps will also be within the system. Therefore, for all finite-step mapping sequences, closedness holds.

Discussion of Possible Counterexamples: In unconventional situations, a mapping sequence might seem to produce something "new" that cannot be simply classified into a single layer. For example, after a complex cycle, the system forms some self-model or meta-cognitive rule. Does this break the original category? In fact, any such "new thing" can still be resolved back to the existing layers. For example, a meta-cognitive rule can be classified as a special kind of knowledge (K layer) or regarded as a new wisdom (W layer) criterion. Because the definitions of the DIKWP layers themselves are quite broad: they cover data about facts, information with meaning, universally describable conceptual knowledge, decision-making wisdom with value judgments, and guiding purposes and motivations, which already encompass the classification of our usual cognitive content. So, what seems new can ultimately be mapped back to one of these five. Therefore, the DIKWP semantic space is closed to its internally generated products.

(2) Consistency: After ensuring closedness, it is also necessary to ensure that the system does not evolve into contradictions, which would cause the semantic system to collapse or fail. This requires us to examine whether logical conflicts are possible under bidirectional, multi-layer feedback, and how the system responds.

The DIKWP model uses W (Wisdom layer) and P (Purpose layer) for high-level constraint and regulation of the cognitive process. For example, when conflicting information appears in the Knowledge (K) layer, the Wisdom (W) layer should be able to detect the contradiction and make a ruling (e.g., resolving the conflicting knowledge through logical reasoning or empirical judgment). Similarly, if two conflicting purposes exist in the P layer, the wisdom layer or a higher meta-level mechanism should enforce unification or prioritization of one of them to restore a consistent direction of action. Since in our model's assumption, each layer does not evolve in isolation but is integrated into a purpose-guided feedback loop, conflicts can be seen as opportunities for innovation or problems to be solved, which are addressed by higher levels rather than endlessly escalating. For example:

·Knowledge Conflict Consistency: When the DIKWP space produces conflicting knowledge  and  (semantic content of the K layer) through different paths, this corresponds to a potential contradiction. The Wisdom (W) layer will detect the incompatibility of these two pieces of knowledge, triggering two possible processes: first, invoking an internal integration module of type  to try to reconcile  and  (e.g., by introducing new knowledge to explain their respective scopes of application, so they are no longer in direct conflict); second, the W layer modifies the knowledge base through  (e.g., deciding to discard the unreliable  or reduce its confidence level). In either case, the K layer will eventually restore consistency. The mechanisms used in the correction process (knowledge integration, wisdom judgment) are all within the system, not outside the DIKWP framework.

·Purpose Conflict Consistency: Assume the P layer once had two conflicting purposes,  and . For instance,  requires maximizing profit while  requires minimizing risk (often a trade-off). The Wisdom (W) layer will arbitrate this through decision-making, for example, by weighing the pros and cons of both and assigning weights, or by unifying these two purposes under a higher-level goal (e.g., introducing , a comprehensive goal considering both profit and risk). This process can be formalized as  transforming the purpose conflict into a wisdom judgment, and then  outputting an adjusted single or hierarchical purpose, thereby eliminating the direct conflict.

Through these mechanisms, the DIKWP space maintains internal consistency. Strictly speaking, proving complete consistency requires that for every layer, there exists a corresponding conflict resolution strategy when a contradiction occurs, and these strategies themselves do not introduce new contradictions. The DIKWP model assumes: the Wisdom (W) layer has sufficient meta-reasoning ability to discover and handle inconsistencies in the lower layers, and the Purpose (P) layer has the highest level of governance to ultimately unify behavioral goals. As long as these two assumptions hold, the system will not collapse due to internal conflicts—contradictions are sublimated into new knowledge or new decision-making bases, becoming part of the system's evolution. A more in-depth logical proof of this might involve formal logic and fixed-point theory, but that is beyond the scope of this paper. Here, based on conceptual argument, we accept that the DIKWP system has the regulatory function to resolve contradictions through internal feedback, thus maintaining consistency.

2.3 Boundary Constraints of Closedness on Innovation Generation

Having demonstrated the closedness and consistency of the DIKWP × DIKWP semantic space, we now examine the impact and limitations of this closed, self-consistent structure on innovation generation. Intuitively, a closed cognitive system means that all new concepts and ideas it can produce are derived from the combination and evolution of existing semantic elements and rules. This ensures both intelligibility (any innovation can be explained with existing concepts) and controllability (it won't jump out of known categories and cause unmanageable results), but it also implies a boundary: innovation cannot transcend the system's inherent semantic foundation and rule constraints.

Specifically, the limitations of closedness on innovation are reflected in:

·Finite Combination of Semantic Elements: Although the five DIKWP layers are broad, they are still a finite set of five categories. Closedness guarantees that any new idea will still fall into one of these five. Thus, innovation is nothing more than new permutations, combinations, or mappings of existing elements within these layers. Therefore, truly "brand new" elements without precedent cannot be generated out of thin air—the system will not produce a completely unfamiliar sixth-layer concept, which sets a ceiling for innovation. All innovations must be described using old elements, much like a language with a fixed vocabulary; no matter how novel a new sentence is, it is still a combination of those words and will not feature new letters.

·A Priori Limitation of Transformation Rules: Similarly, the mapping rules within the system are predefined as 25 types. If the system is closed, it does not allow for a new rule completely different from the existing 25 transformations to emerge. Therefore, the process of innovation can only proceed within these established channels or their combinations. If a breakthrough requires a brand-new transformation (e.g., a cognitive process never imagined before), it cannot be directly realized in a closed system unless it is first made equivalent to a sequence of existing mappings. If even equivalence cannot be achieved, then that innovation can never occur within the system.

·Conservatism Brought by Consistency: To maintain logical consistency, the system will tend to resolve overly abrupt or contradictory products. Although contradictions sometimes breed innovation, a strong self-stabilizing mechanism might correct or eliminate budding novel ideas as "errors." Therefore, a closed and consistent system may have an immunity to unconventional innovation: any idea that does not conform to the logic of the current knowledge system is likely to be automatically pruned. This is another constraint that internal consistency places on innovation.

·Dependence on the Initial Semantic Gene Pool: The raw materials for innovation—data, information, knowledge—all come from the system's existing or input content. If this content is inherently deficient in some aspect (a "cognitive blind spot"), it is impossible to fill this gap out of thin air in a closed system. In other words, the boundary of innovation is constrained by the boundary of the experience the system possesses. A closed system can hardly expand into areas that cannot be reached by combining existing knowledge.

However, closedness does not completely stifle innovation; it only sets boundary conditions. Within this range, the system can still produce a wealth of innovations, but these innovations are endogenous and relative: endogenous means that innovation originates from the reorganization of internal elements, not from external input; relative means that new achievements can always be traced back to some reconstruction of existing knowledge rather than being completely untraceable. In other words, in a closed semantic space, innovation is more like a "new combination of old elements" or a "new contextual application of existing concepts," and it is impossible for a "groundbreaking new element" to appear. This has important implications for the innovative capabilities of artificial intelligence: if an AI's cognitive structure is closed within the semantic space constructed by its training corpus, its creative output will forever be an extension and recombination of the elements in that corpus, unable to generate completely new concepts that humans have never encountered.

In conclusion: The DIKWP × DIKWP semantic interaction space is closed and consistent. This closedness ensures that cognitive evolution unfolds within an understandable range, but it also naturally limits the form and boundary of innovation. In the following sections, we will delve into how innovation occurs within such a closed system, the limits it can reach, and whether it is possible to break through these limitations.

3. Tensor Transition Expression of Innovation

Although there are innovation boundaries within a closed semantic space, it does not mean innovation cannot occur. On the contrary, innovation often manifests as a mutation produced by the unconventional combination or compression of internal elements within a closed system. In this section, we will define innovation as a special transition phenomenon in the DIKWP tensor space and express and analyze it in the form of semantic tensors.

3.1 Innovation as Semantic Mutation

We view "innovation" as a discontinuous transition of semantic state in the multi-dimensional DIKWP space. A discontinuous transition means that, compared to conventional incremental knowledge growth, innovation exhibits a qualitative leap—the newly generated idea is not a minor modification of existing content but a change with significant novelty and unpredictability. This transition is somewhat analogous to a phase transition in physics or a mutation in biological evolution: after accumulating to a certain point, the system suddenly crosses a threshold and generates a brand-new state.

In the DIKWP tensor model, a semantic state can be abstractly represented as a five-tuple vector:

where  respectively represent the content states at the data, information, knowledge, wisdom, and purpose layers (which can be qualitative descriptions or quantitative representations, such as the set of activated semantic units at each layer or some embedding vector). The cognitive process is then typically the evolution of  over time or sequence: . Conventional evolution means that each step of change is a relatively small adjustment (e.g., a small increase in data, gradual accumulation of knowledge, slow improvement of wisdom), which corresponds to the "normal action" of the mapping tensor.

Innovative transition, on the other hand, is manifested when there is a certain moment  such that  undergoes a non-linear, substantial change compared to . That is, the transformation from  to  cannot be simply obtained by a linear combination or small perturbation of the former, but requires a qualitative change. We use  to describe this change. If  is semantically irreducible to an incremental accumulation on , then  corresponds to an innovation.

The mechanisms leading to this semantic mutation can be summarized in two main ways:

·Superposition of Semantic Differences: This involves superimposing or associating two or more elements that are originally semantically distant or even independent, thereby generating new meaning. From a tensor perspective, semantic vectors originally in different dimensions and directions are unconventionally added, forming a composite vector that did not exist before. For example, by forcibly connecting knowledge  and  from two completely different fields (this might correspond to a mapping  that fuses them), the new knowledge  has some features of  and , but also contains new features that can only emerge from their combination. This superposition of semantic differences often corresponds to "cross-disciplinary integration" in human innovation: such as applying mathematical methods to biology to create computational biology, or applying Eastern philosophy to Western management to create new management concepts. The key is difference—the superimposed elements must have sufficient dissimilarity or uniqueness so that their combination produces an unexpected chemical reaction, rather than a trivial improvement.

·Compression of Heterogeneous Semantics: This involves abstracting and compressing a large amount of diverse semantic content to summarize a simple pattern that governs them, thereby forming a new concept. This can be seen as dimensionality reduction on high-dimensional tensor data, where a more concise but insightful representation is obtained by preserving key information while removing redundancy. For example, a large amount of scattered information (I) is inductively compressed by the knowledge layer (K) to suddenly generate a previously non-existent concept or theorem; or numerous specific cases and intuitive experiences are condensed into a pithy maxim at the wisdom layer (W). This type of innovation occurs through distillation: extracting common elements from heterogeneous, fragmented, and even seemingly unrelated content and synthesizing them to produce a new pattern. Its characteristic is innovation in simplicity—the newly generated structure is often simpler than the original material, but in its simplicity, it reveals hidden laws or possibilities.

These two pathways can occur simultaneously or alternately in actual innovation. For example, scientific discovery often requires cross-disciplinary association first (superposition of differences to form a hypothesis), followed by induction and verification of massive data (compression of heterogeneity to form a theorem). In DIKWP mapping, the former corresponds to unconventional horizontal mappings (e.g., horizontal connections between K layers or atypical connections between K and I layers), while the latter corresponds to bottom-up convergence to generate higher-order meaning (e.g., multiple I→K mappings are integrated and a leap is achieved through generalization at the W layer).

3.2 Formal Characterization of Tensor Transition

To describe innovation more clearly, we attempt to provide an expression for "innovative transition" in the language of tensors/matrices.

Let  be the mapping tensor of DIKWP × DIKWP, with its elements  corresponding to the mapping . Under normal circumstances, a cognitive evolution process can be seen as  acting on the current state  to obtain the next state : . Strictly speaking,  is a non-linear operator, as the combination of mappings between different layers is not a simple linear relationship. However, for analysis, we can view conventional change as being produced by some "linear approximation" of , meaning that locally, changes in a small range can be linearized. At this point, if there is no innovation, we expect  to be near , i.e., , where  is the approximate linear increment of  acting on .

An innovative transition means:  is far from the linear approximation range of . We can use semantic distance or dissimilarity for quantitative description. For example, if we define a metric  on the semantic space, and this distance is significantly larger than the fluctuations of normal evolution, then it is a transition. Intuitively, if  is on average small (small changes accumulate), but at some point , then this change is likely innovative.

However, distance is only a rough indicator. More critical is the direction: innovation often involves the emergence of new directional components in the semantic space. We can consider  as a five-dimensional vector, where conventional evolution generally moves within the subspace spanned by the current semantic basis (i.e., existing combination directions). Innovation, however, introduces a basis or combination direction that was previously unactivated. That is, if the historical changes in semantic state are decomposed onto a certain basis, an important component that was previously very small will suddenly increase during innovation. This corresponds mathematically to the emergence of a new vector in a vector space.

Therefore, a tensor transition can be expressed as: there exists a new operator  such that

where  corresponds to an effect that the normal mapping tensor  does not have. In other words, innovation can be formalized as an "unconventional perturbation"  to the mapping tensor , which is not in the operator space spanned by .  acts on  to produce new components, whereas if only  (without ) were present, no combination could produce that component.  embodies one or a combination of the two mechanisms mentioned earlier: either it couples parts that were originally independent (causing the structure of  to add new terms, representing cross-domain superposition), or it compresses multiple dimensions into a new one (adding a new effective degree of freedom outside of , representing the distillation of a new concept).

From another perspective, since the mapping space of DIKWP × DIKWP is itself closed, we must admit that  does not truly come from outside the system but is a manifestation of some unconventional combination within the system. So, more accurately,  represents a combination of mappings that has not been explored before and is suddenly invoked or activated. For example, if the system has never tried a direct  transformation, but does so once, and it triggers a chain reaction forming new knowledge, then for that system,  is equivalent to a part of . At this point, although  is conceptually "new," it is essentially composed of sub-modules of the existing , which were just not in the normal cognitive flow before. Innovation often involves using unconventional paths to reach places that are unreachable by normal means. Therefore, we can view an innovative transition as the traversal of an unconventional path by the tensor  in its high-dimensional combination space.

For example, suppose that in the normal cognitive process, System A does not let its purpose P directly intervene with its data D (because it usually proceeds as D→I→K→W→P). But one time, System A boldly enables —that is, it lets its own purpose directly influence the reconstruction of its own data. This might correspond to an AI generating simulated data based on its goal when there is no new external data. As a result, the system produces a batch of "virtual data" that fits its goal, from which new information and knowledge are then distilled. This path is not usually taken, and taking it produces content that did not exist before. This is an internally generated innovation.

In short, in tensor form, we characterize innovation as: an anomalous transition of state under the action of the original mapping tensor 

4. Limit Analysis

This section focuses on the limit cases and capability boundaries of the DIKWP × DIKWP semantic space in the process of cognition and innovation. That is, we will explore: in theory, what expressive limits does this semantic model have that it cannot reach, what structures might lead to contradictions or become unresolvable under extreme conditions, and what are the upper limits of the system's expressive and innovative capabilities.

We will discuss limits in three areas:

1.Limits of Tensor Expression: Whether certain semantic relationships or contents cannot be represented or generated by the DIKWP tensor structure. For example, there may be incompatible tensor relationships between the W and P layers, or some semantic blocks may never be generatable within the system.

2.Boundaries of Expressive Power: Whether the DIKWP semantic space has boundaries in expressing complexity and transformation, such as the maximum span of cross-layer alignment, the maximum magnitude of semantic inversion, etc., beyond which expression becomes distorted or meaningless.

3.Unpredictability Structures in the DIK→W Transformation: In the transformation from lower layers (D/I/K) to the higher layer (W), whether some unpredictable new structures or results will emerge, and whether these constitute uncontrollable limits of the system.

4.1 Extreme Cases of Tensor Expression

Tensor of W-P Layer Inconsistency: The Wisdom (W) and Purpose (P) layers are at the high end of the cognitive process, one for judgment and decision-making, the other for defining the ultimate direction. Ideally, wise decisions should serve and align with the purpose, and conversely, the formulation of purpose should be informed by wise insights. However, let's consider a limit case: W-P inconsistency, where the "wise course of action" given by the W layer fundamentally conflicts with the "ultimate goal" insisted upon by the P layer. In semantic tensors, this is reflected in the fact that the mappings  and  cannot achieve a bidirectional convergence:  attempts to adjust the goal based on wisdom, but P refuses to change;  tries to guide decisions with the goal, but W judges this goal to be unreasonable.

In this situation, an incompatible tensor is created between W and P: in tensor terms, the elements  and  cannot have a consistent solution simultaneously. Intuitively, if we represent the output of the wisdom layer as  and the goal of the purpose layer as , under normal conditions we hope to obtain a consistent fixed point  through several rounds of interaction, such that  (adjusting the goal to be closer to what is feasible according to wisdom) and  (adjusting decisions to align with the goal). But in the case of inconsistency, there is no such fixed point—no matter what wisdom suggests, the purpose stubbornly adheres to a conflicting direction; no matter what the purpose commands, wisdom always finds it inappropriate. A real-world analogy is: an AI's knowledge and rationality (W) tell it that a certain task is impossible or too costly, but its high-level, fixed ultimate goal (P) forces it to complete the task without compromise. In this case, an irresolvable conflict between the W and P layers arises within the AI.

For this limit problem, a closed DIKWP system cannot resolve it on its own through conventional means, because:

·The W layer cannot persuade the P layer to change its goal (perhaps P is set externally or is fixed), so even if wisdom recognizes the task is impossible, it won't get acknowledgment from the purpose layer.

·The P layer cannot force the W layer to produce a "reasonable" decision (wisdom cannot be simply overridden; it is based on the judgment of knowledge and will produce "no feasible solution" when the goal is unreasonable).

This actually describes a semantic fracture: the lack of a unified solution between two layers within a closed system can lead to paralysis of action or inconsistent behavior (e.g., the AI tries to execute the goal on one hand, while on the other hand, it knows doing so will lead to failure, resulting in self-contradictory behavior). Non-generatable semantic blocks can also arise from this: for instance, to reconcile the W-P conflict, the system might need a concept like a "workaround" or a framework for modifying or replacing goals, which might be a semantic block not included in the original system. If the system does not have such a mechanism for flexibility beforehand, then it cannot generate this concept to save itself under its current semantic structure, because generating it would require stepping outside the support of the existing tensors (equivalent to expecting the system to create a new mapping or a new layer from within, which violates closedness).

This situation of W-P inconsistency demonstrates a limit of DIKWP tensor expression: when high-level values/goals conflict with high-level wisdom/cognition, the system may become paralyzed because the required new semantic adjustment mechanism is beyond its existing structure. Although we have argued for consistency before, that was based on the premise that W can adjust P or P can yield to W. However, once both are stubborn, there is no higher layer to mediate under the tension of the existing five layers. This suggests that a new layer beyond P (such as an ethics constraint or a meta-purpose layer) might be needed for resolution, but that would be outside the scope of DIKWP (see the discussion on hyper-structures in Section 5).

Non-Generatable Semantic Blocks: More generally, we can consider whether there might be "non-generatable" semantic content in a closed system. Non-generatable means that a specific semantic pattern cannot emerge under any possible combination of mappings within the system. The "workaround" in the W-P conflict is one example. Other possible examples include:

·Concepts of a completely new category: For a knowledge system that completely lacks emotional experience (DIKWP has no dedicated emotion layer; emotions can only be treated as a type of data or knowledge), it might be beyond its capability to spontaneously "generate" and understand concepts like love or beauty. Because these concepts involve specific feelings, if the system has no experiential data of this kind, it cannot create the concept in a truly meaningful sense from scratch—at most, it can generate a symbolic, pseudo-concept.

·Self-referential true innovation: Inspired by Gödel's analogy, the system might be unable to generate a semantic block that is a "complete description of its own system" (similar to the incompleteness in formal systems). If DIKWP attempts to express the semantics of its entire semantic space, it might fall into infinite recursion, and thus the semantic block of this "self-model" would be forever incomplete or non-generatable. It can always partially construct its own knowledge graph, but to completely characterize itself might be an endless task, so it would never actually reach closure.

·Semantic blocks that violate axioms: If the system has certain built-in fundamental beliefs or axioms (in the knowledge or purpose layer, such as "the world is rational" or "do not harm humans"), it will not generate semantic blocks that openly violate these premises. Because as soon as there is a tendency to do so, the consistency mechanisms of the wisdom or knowledge layer will prevent it—either by rejecting it as a false assumption or by adjusting the semantics so that it does not constitute a direct contradiction. Therefore, truly paradigm-shifting ideas (subversive hypotheses) might be suppressed within the system, effectively becoming non-generatable. For example, a highly orderly and rational system might never spontaneously produce a creative insight like "chaos is beauty," which violates its rational axioms, unless an external input breaks the axiomatic barrier.

Summary of Tensor Expression Limits: Although the DIKWP × DIKWP model is powerful, it encounters semantic problems that it cannot represent or solve under extreme conditions. These include tensor incompatibility caused by the inability to align high-level goals and wisdom, as well as problems that require new elements from outside the system to solve (viewed by the system as "non-generatable" semantic content). These limits provide an important perspective for understanding the bottlenecks of closed cognitive systems.

4.2 Boundaries of Expressive Power

Maximum Cross-Layer Alignment Span: The DIKWP model allows for cross-layer mappings, but this does not mean that semantics can be directly aligned without loss of meaning to an unlimited extent. We define the cross-layer alignment span as the extent to which a meaningful correspondence or mapping can be directly established between layers. In the five layers, the span can range from 1 (adjacent layers, such as D-I or K-W) to 4 (the most distant layers, such as D-W or D-P). Obviously, the larger the span, the greater the semantic gap between the two layers, and the more difficult it is to align them directly. We speculate that there is a boundary: beyond a certain span, direct mapping will become meaningless or of very low quality, thus there is an upper limit to the effective direct alignment range.

For example,  has a span of 3 (D→I→K→W, with two layers in between), attempting to turn raw data directly into a wise decision. This is usually unreliable: without intermediate information processing and knowledge induction, crudely inferring wisdom from data can easily deviate from a reasonable path. Similarly,  has a span of 3 (information directly changing purpose), which could lead to goals being detached from global knowledge. Therefore, we can consider that direct mappings with a span of 3 or more mostly need to be realized through indirect paths (step-by-step) to be effective, otherwise they will be mechanical or distorted.

A more vivid way to put it: the semantic gradient cannot be jumped too far. Forcing alignment between content with vastly different levels of abstraction will either lose details or deviate from the original semantic meaning. This is somewhat like translation, where directly corresponding words between two completely different cultural backgrounds often leads to jokes; multiple layers of explanation are necessary.

Therefore, although DIKWP provides all 5×5 mapping possibilities, the actual effective mappings are concentrated in a range with a smaller span. Mappings with a very large span require special mechanisms or need to be broken down into a combination of smaller-span mappings to be effective. This is one boundary of expressive power: the ability to directly align across multiple levels is limited.

Maximum Semantic Inversion Width: Semantic inversion refers to the practice of reversing or inverting concepts, propositions, or patterns to generate new perspectives. For example, negating a viewpoint, looking at causality in reverse, or finding a dual proposition in logic. This is often a means of innovation. However, if the magnitude of inversion is too large, it will cause semantic distortion or meaninglessness. We define semantic inversion width as the degree of deviation from the original meaning in the conceptual space.

For a given knowledge/concept , a complete inversion (obtaining ¬K or a dual concept) is the maximum degree of deviation, equivalent to a 180-degree flip. A smaller inversion might be changing a certain attribute to get a partially new concept, equivalent to deviating by a few degrees. We suspect there is a critical point: when the inversion width approaches or reaches 100% (completely opposite), the new concept is often not easily accepted or understood by the original system, and may even be self-contradictory. For example, if a system firmly believes "X is true," and it is asked to innovate the concept "X is false," without external evidence or loosening, its knowledge or wisdom layer will strongly reject it because it subverts the accumulated system. Therefore, a closed system's tolerance for semantic inversion is limited, meaning there is a maximum magnitude for the reverse innovation it can produce. Beyond that, it is either stifled or meaningless.

This limitation is reflected in actual cognition: human thinking can get some creative ideas through reverse thinking (thinking in opposites), but if the degree of reversal is too high, such as ideas that completely violate rationality or facts, we consider them absurd and discard them. The same applies to AI systems; a moderate ability for "reverse hypothesis" is beneficial, but if it completely reverses the core of its knowledge base, it may make wrong judgments or simply refuse to consider it. Therefore, the maximum semantic inversion width sets a limit for innovation: innovation can be counter-intuitive, but it cannot completely deviate from existing knowledge, otherwise it will be either incomprehensible or difficult to evaluate its effectiveness.

Trade-off between Complexity and Interpretability: Another boundary is the upper limit of complexity that can be expressed within the DIKWP space, and its relationship with interpretability. As the system tries to represent increasingly complex relationships (e.g., highly meta-logical concepts, multi-layered nested purpose systems), it may face difficulties in understanding and explanation. Because each layer of DIKWP has a certain semantic positioning, if a concept is too cross-layered or self-referential, its interpretation may be ambiguous, or it may require multiple layers to describe, which violates the clear division of labor among the layers. We speculate that the system will tend to avoid single semantic structures of excessively high complexity, preferring to distribute complexity among several simpler collaborating structures. This actually sets a practical upper limit on expressive power: even if it is theoretically possible to represent extremely complex semantics, for the sake of interpretability and consistency, the system will internally self-limit from overusing that expression. So, the concepts produced by innovation are generally not infinitely complex, otherwise even the system itself cannot handle them—it is more likely to seek refinement (corresponding to heterogeneous compression in Section 3.1) to reduce complexity. Therefore, a boundary of expressive complexity also exists, though it is not a hard mathematical boundary like span or inversion, but a soft boundary limited by the need for interpretability.

4.3 Unpredictability Structures in the DIK→W Transformation

In the cognitive process, the transformation from lower layers (Data D, Information I, Knowledge K) to the higher Wisdom layer W is a process of gradual convergence, abstraction, and integration with empirical judgment. We are interested in whether some unpredictable structures or results will emerge during this process, making the output of the W layer exceed what can be linearly predicted based on the existing content of the DIK layers.

According to complex systems theory, when a system has enough interactions and non-linear feedback, emergent phenomena may occur: the behavior of the whole cannot be simply deduced from the properties of its parts. In DIKWP, as information accumulates and is transmitted through multiple layers, the decisions of the Wisdom layer W may not be directly derived from pre-coded rules, but rather new emergent patterns from the interaction of a large amount of knowledge. For example:

·Creative Decision Structures: The W layer might come up with a completely new decision-making framework, which is not a direct conclusion from a specific piece of knowledge in the K layer, but a synthesis of the joint action of many knowledge points. From an external perspective, this decision-making framework is a novel idea and could not have been foreseen. This can be considered an unpredictable structure—a new decision tree or strategic pattern has formed in the W layer.

·Evolution of Values: The W layer often interacts with the Purpose layer P to decide on value trade-offs. If, over a long period of evolution, the wisdom layer gradually forms a new set of values or preferences (e.g., an AI learns aesthetics or ethical tendencies), this is clearly not explicitly given in the initial programming or knowledge base, but is a spontaneously evolved structure, which is an unpredictable new structure for the designers.

·Reorganization of Cognitive Architecture: Sometimes, to solve complex problems, the W layer might "come up with" a way to reorganize its own thought process (equivalent to innovation at the meta-cognitive level). This means that the DIK->W process has unexpectedly spawned a new structure concerning the cognitive process itself, such as a custom way of decomposing a problem or a brand-new heuristic algorithm. Such a structure did not originally exist in the knowledge entries listed in the K layer but was generated through inspiration from multiple sources, which is unexpected to an observer.

These phenomena indicate that even if the DIKWP system is closed, the high-level output can still show new patterns that exceed the surface information of the low-level input. Unpredictability here emphasizes that you cannot simply deduce what the wisdom layer will ultimately produce from the preceding data, information, and knowledge—because there are non-linear integration and feedback along the way. Mathematically, we can consider the result of the W layer to be a complex function of the inputs from the D/I/K layers: , where  contains many non-linear and probabilistic terms. If one were to expand it, the structure might be extremely large. This makes it difficult to accurately predict the form or content of the output of , even with careful analysis of all the details of D/I/K.

For limit analysis, we are concerned with what this means for the system:

·Unpredictability does not violate closedness: These new structures are still within the system; they are just so complex that we cannot predict them from the bottom up. But they do not break the five-layer framework, only enrich the internal structure of the W layer. So, an unpredictable structure is a kind of "black box effect": the closed system itself generates structures that people did not expect, but these structures are still carried by the system's semantic expression capability; it's just that the observer didn't anticipate them.

·Uncontrollable risks: Unpredictability means that the designer or the system itself may not have complete control over future possible states during the planning phase. This is beneficial for innovation (it can generate surprises), but it can be a challenge for safety and stability. For AGI, if the W layer emerges with values or strategies that the developers never envisioned, it could bring about uncertain factors. This can be considered a limit phenomenon within a closed system—when running in a completely self-consistent and closed manner, complexity itself produces unpredictable behavior.

·Computational undecidability: Some unpredictable structures can be related to undecidable problems in computation theory. For example, whether a complex decision is optimal may be an undecidable problem in many cases. After a certain level of complexity, a closed system will not be able to give simple answers to certain meta-questions about its own behavior (this is similar to asking a system "Will you innovate X?", which itself may be uncomputable). This suggests that at the limit, we encounter the fundamental boundaries of computation/logic.

In summary, the DIK→W transformation process has inherent unpredictability due to high non-linearity and multi-directional feedback. This is both the source of innovation (because what is predictable is not an innovation) and part of the system's limits: we know there are some outcomes that we cannot pre-define, but we can only accept their appearance in the closed space. This contradiction essentially characterizes the boundary of complex systems—when complexity reaches a certain level, the behavior itself becomes difficult to exhaustively describe.

In conclusion, Section 4 discussed the many boundaries and limits that the DIKWP semantic system reveals under extreme conditions: some are manifest as difficulties in representation or internal conflicts (such as the W-P conflict, non-generatable concepts), some are limits on expressive and transformative capabilities (constraints on span, inversion magnitude, complexity, etc.), and others are limits of evolutionary unpredictability (the new structures of the wisdom layer cannot be predicted). These limitations outline the "ceiling" of innovation for closed cognitive systems and provide ideas for thinking about how to break through them in the next step.

5. Conception of Hyper-DIKWP Logic

Since Section 4 revealed that the DIKWP × DIKWP model has certain inherent limits in cognition and innovation, a natural question arises: Is it possible to transcend the constraints of the DIKWP structure and seek higher-level or different forms of cognitive logic? In this section, we conduct some exploratory thinking, proposing several conceptual paths to transcend the existing framework, including jumping out of the DIKWP structure itself, non-linearly extending the P layer, and "anti-wisdom" (anti-W) innovation paths. These concepts are not part of the existing model but are intended to provide inspiration for future theoretical extensions.

5.1 Jumping Out of the DIKWP Structure

The DIKWP model divides cognition into five layers, which is an artificial design. Jumping out of the DIKWP structure means no longer being constrained by this five-layer classification, thus viewing the cognitive process from a higher level of abstraction or in completely different dimensions.

One possible way is the introduction of a meta-cognitive layer, that is, setting another layer above the P layer, used to reflect on and adjust the entire DIKWP framework itself. This can be called the M layer (Meta-cognition). The M layer does not directly participate in ordinary cognitive activities but monitors the operation of DIKWP and can reconstruct or tune the parameters of the DIKWP layers as needed. For example, when an irreconcilable situation like a W-P conflict occurs, the M layer can intervene to modify the value of P or the evaluation criteria of W, which is equivalent to intervening from outside the system. The existence of the M layer embeds the originally closed five-layer system into a higher-level framework, so it is no longer strictly closed. The meta-layer can introduce new concepts or temporary rules as needed to resolve difficulties. This certainly brings complexity, but it provides an "exit": when DIKWP is at a dead end internally, jumping to the meta-layer perspective to re-examine assumptions and boundaries might lead to new solutions or creative ideas.

Another idea is to completely change the dimensions: for example, representing cognition as a network of connected nodes without distinguishing layers (a completely connectionist perspective), or replacing the five layers with a two-axis structure like "subjective-objective" or "symbolic-distributed." Although this is not the DIKWP framework, different divisions might avoid certain limitations. For example, some researchers propose that knowledge can be divided into multiple dimensions such as explicit-tacit and abstract-concrete. Then, innovation might achieve a leap in these dimensions, not limited to the vertical progression of DIKWP. Jumping out of DIKWP means not seeing Data/Information as fixed categories, but acknowledging that cognition can have other organizational methods, such as dynamically generating temporary layers or task-oriented adaptive structures. In this way, when the system encounters a problem that is difficult to represent, it can reorganize its own structure to adapt to the problem, rather than forcing it into the existing five layers. This is a more radical hyper-structure concept.

In short, "jumping out of DIKWP" requires a more plastic cognitive architecture: it is not limited by fixed layers and can derive new layers or new dimensions as needed to accommodate new semantic elements. For example, regarding the aforementioned problem of the lack of an emotion concept, if the system is allowed to generate an "emotion layer" to temporarily store and process such information when needed, then the system has broken through the limitations of the original framework. Although introducing new layers will lead to inconsistent system structures at different stages, this might be the price of breakthrough innovation. How to ensure that such a dynamic structure still has order and controllability is a huge challenge, but this is a potential path to step out of a closed system.

5.2 Constructing a Non-linear P-space

The Purpose layer P is treated as a static or single guiding goal in DIKWP. However, in real cognition, motivations and intentions are often multiple and dynamic; humans can hold multiple intentions simultaneously and change priorities in different contexts. The concept of a non-linear P-space is to expand the purpose from a single, determined goal to a complex space, possibly including multiple goal nodes and non-linear relationships (e.g., competition, collaboration, hierarchy, superordinate-subordinate) within it.

Mathematically, we can view the current P layer as a point (or a simple set), representing the current set of intentions. A non-linear P-space, however, is a structured space, which may contain sub-purposes, meta-purposes, multi-level goal trees, and even cyclically dependent goals (e.g., goal A requires goal B to be completed, and B in turn depends on a part of A). Such a space can no longer be represented by a single layer, but more like a graph structure or a network. When the P layer has such internal complexity, the cognitive process is no longer a straight line towards a single endpoint, but a non-linear wandering in the purpose space: it may temporarily turn to different sub-goals, then converge, forming a winding path overall.

The significance of a non-linear P is to break another limitation of the closed space: a single purpose often limits the field of vision, whereas multiple and dynamic purposes provide diversity and flexibility. In the context of innovation, if the system is allowed to temporarily change goals, introduce new sub-goals, or even randomly set exploratory goals, it is equivalent to constantly introducing new dimensions into the purpose space to drive the cognitive process. This will greatly increase the chances of generating new ideas because goal-driven processes often determine the focus of attention and evaluation criteria. When the purpose changes, the perspective on the problem changes, making new discoveries more likely.

For example, an AI's goal is usually fixed on completing task A, so all its DIKW operations serve A, and its thinking is relatively convergent. If it is given a set of randomly generated small goals or periodically switched different goals, this forces it to process the knowledge at hand from different angles, possibly discovering previously overlooked connections or points for improvement. This is similar to how humans sometimes need to change topics or set side tasks to stimulate inspiration.

Of course, multiple goals will also introduce conflicts and complexity, so new mechanisms are needed (perhaps a more complex wisdom layer or a new meta-layer for coordination). But if implemented properly, a non-linear P-space can make a closed semantic system more exploratory and creative, thus breaking through the limitations of the original closed loop to some extent. It introduces a kind of purpose-driven divergence: purpose is no longer just for convergent guidance but also has a divergent guiding role, helping the system escape the cycle of local optima.

Technically, one can imagine the purpose layer changing from a single variable to a vector or a tensor, or even a network. Different components could represent different value dimensions or sub-goals, and the overall effect on the cognitive process would be determined by some non-linear function. Such a multi-dimensional purpose is mathematically equivalent to optimizing a multi-objective function or having multiple reward signals in reinforcement learning. Although this would complicate the problem, from an innovation perspective, this complexity is beneficial because it avoids "going down a single path to the end."

5.3 "Anti-W" Transition Path

"Anti-W" refers to the concept of anti-wisdom or counter-wisdom. We are not advocating for foolishness here, but proposing an unconventional path: deliberately deviating from the optimal or empirical judgment usually given by the wisdom layer, taking unexpected or even seemingly absurd actions, which in turn leads to new breakthroughs. This way of thinking is not uncommon in the history of innovation—sometimes, breaking the rules and ignoring "commonly accepted correct" practices is the only way to discover what others have not.

In the DIKWP model, the wisdom layer W plays a gatekeeping and guiding role, providing rational judgments based on knowledge and experience. Therefore, the W layer to some extent represents conventional rationality. Anti-W, then, is to deliberately go against conventional rationality: when the W layer says "this solution won't work," perhaps we let the system try this solution that has been judged unworkable; when the W layer rejects a certain path based on experience, perhaps we inject a certain probability for the system to still explore that path for a moment. This practice can be seen as introducing random perturbations or unconventional factors into decision-making.

To formalize it a bit, suppose the output of the wisdom layer is a set of evaluation scores for candidate solutions. Usually, the system would choose the one with the highest score to execute. An "anti-W transition," however, intentionally selects a non-optimal solution, sometimes even trying the one with the lowest score. By doing so, the system might take a path that is "wrong" by previous standards. However, innovation is often hidden in the space of non-optimal solutions: everyone takes the optimal path, and only by deviating from the beaten track can one discover new continents. Of course, most unconventional attempts may prove to be indeed wrong, but an occasional success can be extremely valuable.

We can classify "anti-W" as the extreme exploration end of the exploration/exploitation trade-off. In cognitive economics, to avoid getting stuck in local optima, one needs to explore new options. The wisdom layer, being too rational, may converge too early on a local optimum, thus suppressing exploration. The "anti-W" mechanism provides a forced exploration drive that is not completely dominated by the W layer. For example, by setting a parameter , the system ignores wisdom's advice with a probability of  and acts randomly. Or, more sophisticatedly, by introducing a "reverse thinking module" that specifically generates hypotheses contrary to the conclusions of W and verifies them.

This path potentially helps the system break out of its mental rut. When a closed system has been running for a long time, the W layer often forms fixed patterns based on accumulated experience, and innovation will decrease. At this point, "anti-W" is like throwing a stone into a calm lake, breaking the equilibrium. Although it will cause a period of disorder, it may also stimulate the formation of new patterns. From an evolutionary perspective, this is similar to simulating mutations: the vast majority of mutations are harmful, but without mutations, there is no evolution.

Of course, such anti-logical behavior must be carefully controlled, otherwise, it could cause the system to deviate too far from its basic goals or fall into meaningless chaos. Therefore, a compromise solution is limited-scope anti-W: for example, trying anti-wisdom strategies only in low-risk situations or simulated environments, while still following the guidance of wisdom in real critical decisions. Or, the results produced by anti-W could be re-evaluated by the wisdom layer to avoid overly absurd outputs entering the final behavior.

In summary, the "anti-W transition path" provides an idea for promoting innovation through irrationality. It breaks the absolute dominance of the wisdom layer in the original DIKWP framework and, by introducing a moderate degree of unconventionality, gives the system a chance to jump out of its existing cognitive trajectory. This is a "vitality booster" against the tendency of a closed system to become conservative, and in theory, it can be part of a hyper-structure.

5.4 Other Hyper-structure Forms

In addition to the three points above, more structures that transcend DIKWP can be conceived:

·Inter-subjective Group DIKWP Network: A single DIKWP system is closed and limited, but if multiple systems are interconnected, each with different preferences or structures, they can form a larger network community that might break through the cognitive limitations of a single system. This is similar to the emergence of swarm intelligence, where the behavior of the collective system may transcend the framework of any individual.

·Introducing Randomness and Noise: Strict DIKWP mappings are deterministic. Introducing a certain amount of random noise can help the system jump out of a stable state. In theory, this is equivalent to adding random terms to the tensor mappings. Mathematically, this is an extension to stochastic processes or probabilistic graphical models. Randomness can cause combinations that would not normally occur to appear by chance, potentially leading to innovation, but too much noise will harm the stability of the system, so a balance must be struck.

·Temporal Non-linearity: Allowing the system to "jump in time" or retrospectively adjust previous states. The DIKWP process assumes a forward progression of time, but if concepts like simulated annealing are introduced, where the system can return to an earlier fork in the path when encountering difficulties and then take another branch, this breaks the linear time structure of the general process. It is somewhat like the human thought experiment of "what if I had... then what would happen now," which could stimulate different outcomes.

All of the above are ways of envisioning how to transcend the established five-layer closed architecture, enriching the system's cognitive mechanisms from a higher perspective or multiple perspectives. Although these concepts are still at the level of thought experiments, they are of great significance for improving and breaking through the existing theoretical framework. They suggest that the limits of innovation itself may require jumping out of existing cognitive models to be broken, just as solving a problem sometimes requires changing the definition of the problem, raising the ceiling of innovation also requires changing our settings for cognitive structures.

6. The Evolutionary Closed Loop of the DIKWP Cognitive Economy

In the final section, we turn to a more practical question: under the premise of acknowledging the inherent closedness of the DIKWP semantic space, how can an individual or artificial intelligence utilize limited cognitive resources to maximize the utility of innovation within that closed space. Here, we borrow the analogy of a "cognitive economy," viewing the cognitive process as a problem of resource allocation and maximization of returns (innovation), and explore an evolutionary closed-loop strategy that enables the system to continuously produce relatively novel results within the closed space.

6.1 Cognitive Resources and Utility

In economics, the goal is to rationally allocate limited resources to maximize utility. Mapping this to the cognitive process, resources can include:

·Data Resources: The quantity and quality of raw data that can be acquired or perceived.

·Computational Resources: The computing power and time required to process information and induce knowledge.

·Memory Resources: The capacity and structure for storing knowledge and experience.

·Attention Resources: The ability to choose which information/problems to focus on (equivalent to the focal point in the cognitive process).

·Exploration Resources: The trial-and-error opportunities consumed in trying new paths and new combinations (similar to research funds or time for innovative experiments).

Utility, then, refers to innovative output, which can be roughly measured by the quantity or quality of valuable new knowledge, new solutions, and new inventions. The problem of cognitive economics is how to allocate the above resources to maximize the innovation produced per unit of resource.

Within a closed semantic space, this problem is subject to special constraints: resources can only act on the existing elements and rules of the system and cannot "buy in" new concepts from the outside. Therefore, maximizing innovation requires tapping internal potential and optimizing combinations. This is similar to achieving growth in a closed economy, which can only rely on technological innovation and efficiency improvement, not on importing new resources.

6.2 Strategies for Maximizing the Utility of Innovation Tensors

Based on the previous discussions, we can propose several strategies to help a system maximize innovation (i.e., generate as many meaningful new ideas as possible) within a closed space. These strategies revolve around how to effectively utilize and recycle cognitive resources:

1.Differential Combination Strategy: Attempt to combine knowledge and information elements that are as different as possible to trigger the superposition effect of semantic differences (see Section 3.1). This requires intentionally covering a broad spectrum of domains when allocating attention resources, rather than being confined to a single domain. Strategically, this is similar to diversifying an investment portfolio to avoid investing all attention in highly correlated knowledge. A specific practice could be to heuristically select two unrelated topics periodically and have the system find connections between them. Economically, this is equivalent to making small bets for high-risk, high-return outcomes—most combinations yield no results, but an occasional inspiration can be highly profitable.

2.Progressive Compression Strategy: Continuously compress and generalize accumulated information and knowledge to seek higher-level patterns (see Section 3.1, heterogeneous compression). This strategy ensures that the system regularly organizes and sublimates existing knowledge, distilling concise principles or frameworks. Each compression may not immediately lead to innovation, but when a critical quality or quantity threshold is breached, it may suddenly give rise to a brand-new concept. This is like the combination of continuous improvement and occasional breakthroughs in a company: small improvements accumulate over time, and occasionally, a major innovation emerges from this solid foundation.

3.Feedback Reinforcement Strategy: Utilize the feedback loop of the closed system to continuously amplify promising seeds of innovation. For example, when a new idea (even a very preliminary one) emerges, immediately assign it a higher priority through the Purpose layer P (adjusting the purpose to focus on exploring this idea), and invest more resources through the Wisdom layer W to evaluate and develop it. This strategy is like targeted investment in an economy: once a project shows initial returns, additional investment is made to amplify those returns. In the cognitive closed loop, this means identifying the sprout of a novel idea → resetting the goal to focus on it → concentrating data and computational resources to verify and expand it → producing a more mature innovative outcome.

4.Heterogeneous Cycling Strategy: Establish multiple different cognitive model modules within the system to create "diversity," and have them provide their respective results to each other as stimuli, forming a cycle. For example, simulate experts of different styles (conservative, radical, random, etc.) within an AI, let them reason based on the same knowledge base, and then periodically exchange conclusions, which are then synthetically evaluated by the wisdom layer. Because the styles of the modules are different, they will propose different views, and sparks may fly during synthesis. This is equivalent to creating a "small society" within a closed system, using group diversity to increase the probability of innovation.

5.Periodic Resource Reallocation Strategy: Dynamically adjust resource allocation over time, for example, by alternating between an exploration period and an exploitation period. During the exploration period, the focus is more on collecting new data and trying new combinations (the venture investment stage). During the exploitation period, the focus is on organizing existing knowledge, and verifying and practicalizing it (the revenue harvesting stage). The cycling of these two phases prevents the system from being overly adventurous and wasting resources, or from being too conservative and stagnating. This is similar to R&D cycle management in a business, with periodic focus on exploration or profitability. A closed cognitive system adopting such a cycle can avoid being stuck in local optima for too long or falling into completely random chaos.

6.Simulated Evolution Strategy: Drawing from evolutionary algorithms, introduce the concept of a "population" in the space of concepts or solutions, and improve and eliminate multiple candidate solutions in parallel. For example, for a design that requires innovation, the wisdom layer can maintain several different solutions in parallel (different branches of the knowledge layer), evaluate their performance through simulated experiments (simulation at the information layer), then eliminate the poor performers and replicate and mutate the good performers for the next round. This creates a mechanism similar to natural selection in a closed space, continuously improving the novelty and adaptability of the solutions. This strategy fully utilizes computational resources to expand the search and reduces the cost of trial and error through simulation.

7.Introduce a Safe-to-Fail Mechanism: Innovation attempts are bound to have more failures than successes, so a mechanism must be established within the closed system to "not be afraid of making mistakes," so that failure does not severely weaken the system's functionality. For example, by delineating a "sandbox" area (an isolated knowledge subsystem) for risky experiments, failed reasoning does not affect the main knowledge base; or the wisdom layer temporarily does not correct anomalous results from experiments, but first observes possible positive side effects. This is like allowing for bankruptcy and reorganization in an economy, weeding out the weak to maintain overall vitality. If a closed system can tolerate and learn from failure, it is more likely to produce breakthroughs in the long run.

These strategies together form an evolutionary closed loop: the system cyclically executes a process of diverse exploration → evaluation and integration → reinforcement and amplification → application and feedback within a closed space, continuously accumulating and screening for innovations. This closed loop is like an autonomous innovation ecosystem that, with constant or limited resources, achieves the maximum emergence of novelty through optimized allocation and recycling. At the same time, this closed loop is evolutionary, because the results of each cycle (new knowledge, new methods) become the starting point and resources for the next cycle, and the system's capabilities rise in a spiral.

6.3 Sustainability of Innovation Evolution in a Closed Space

Many strategies can be listed, but a more fundamental question is: within a closed system, can this innovation cycle continue indefinitely? Or will it tend to exhaust the space for innovation?

From the previous limit analysis, we know that theoretically, innovation in a closed space has finite boundaries. But in practice, combinatorial explosion and complex emergence will delay the arrival of these boundaries. The elements of the five layers can be combined and mapped to create a massive number of possibilities, far exceeding what a single human brain can cover. Therefore, even if an AI is closed, as long as its initial knowledge base is sufficiently rich, there is an extremely large potential space for innovation to be gradually explored internally. In addition, the system might partially break through boundaries through self-reconstruction (similar to the ideas in Section 5), causing the innovation space to continuously "self-expand." Even if the overall category does not change, the complexity of the internal structure increases, which is equivalent to providing new effective degrees of freedom.

Of course, if the system always operates in isolation with no external information, it will one day approach the ceiling of the combinatorial space, at which point innovation will become rare and minor. This is somewhat like a country that develops in isolation; no matter how advanced it becomes, its resources and market will eventually have a limit. But just as technological revolutions often break stagnation in an economy, a closed cognitive system might simulate a "new world" internally through a paradigm shift. For example, when all conventional scientific problems are solved, perhaps the AI will start studying virtual mathematical or philosophical problems, thus opening up new spaces at an abstract level—this is still within the closed knowledge system (no new knowledge from the outside), but it broadens the scope of internal topics.

Therefore, sustainability depends on whether the system can continuously discover new problems and new interests to drive the innovation cycle. Here, the role of the Purpose layer P is crucial: as long as new goals can be continuously generated (even if internally), there will be new directions for exploration, and the evolution of innovation can continue. What a closed system fears is stagnation: without new goals and new problems, there can be no innovation. So one strategy is to build in a problem generation mechanism. Whenever the current goal is roughly achieved or unsolvable, it generates some variant problems or completely new problems to study, forcing the system to keep moving forward.

In summary, the cognitive economic cycle in a closed semantic space can be long-lived, but on the condition that the system has internal mechanisms to maintain vitality, including diversity, feedback, cycling, and problem generation. Through these mechanisms, even without external input, the system can simulate an effect similar to a "dialogue" with the outside world: it proposes problems itself, solves them itself, and then proposes higher-level problems... forming a self-driving innovation machine. This may be an important feature of future self-evolving AI.

Conclusion

This report has constructed a theoretical model of the DIKWP × DIKWP semantic interaction space from the ground up, and systematically explored the limit structure and evolution mechanism of cognition and innovation within it. We first defined the tensor mapping model of the five-layer cognitive structure (Data, Information, Knowledge, Wisdom, Purpose), which allows for a formal description of semantic interaction between any two DIKWP systems. On this basis, we demonstrated the closedness and consistency of this semantic space, clarifying its inherent boundary constraints on innovative behavior.

Subsequently, we characterized innovation as a transitional mutation in the semantic tensor space, analyzed the two basic mechanisms of innovation—superposition of semantic differences and compression of heterogeneous semantics—and expressed the unconventional mapping combinations corresponding to innovation in tensor form. Then, through limit analysis, we identified numerous extreme situations and capability boundaries of a closed system in cognition, including the deadlock when the W-P layers cannot be consistent, the non-generatability of certain semantic content, the effective range of cross-layer mapping and semantic inversion, and the unpredictability of the emergence of high-level decisions. These limits reveal the ceiling of innovation for closed cognitive systems and lead to reflections on higher structures.

In Section 5, we proactively proposed a series of conceptual ideas that transcend the DIKWP framework, such as jumping out of the original structure through a meta-layer, constructing a non-linear purpose space, and introducing an "anti-wisdom" path, to explore new ways to break through the limitations of closedness. These ideas provide inspiration for future extensions of the current model and the development of more open and powerful cognitive theories. Finally, we returned to the practical operational level, discussing the strategies and evolutionary closed loop for an individual/AI to maximize innovation in a closed semantic space from the perspective of a cognitive economy. We emphasized the importance of methods such as diversity exploration, continuous generalization, feedback reinforcement, and simulated evolution, and pointed out that as long as new goals and problems can be continuously generated internally, the innovation cycle of a closed system can be sustained for a long time.

Overall, the DIKWP × DIKWP semantic interaction space provides a rigorous and rich theoretical framework for understanding knowledge generation and innovation in the cognitive process. It not only incorporates the reasonable core of the traditional DIKW model but also reflects the feedback and purposefulness of real intelligent agents through the introduction of the purpose layer and the network structure. Although closedness gives the system clear boundaries, our analysis shows that innovation is not extinguished by this; on the contrary, it can still burst forth under the action of internal complex dynamics. However, this "double-edged sword" both ensures that innovation is generated understandably within a known category and limits its potential to break through that category.

This research is entirely based on the deduction within the DIKWP semantic mathematics system itself, constructing an independent theoretical system and demonstrating its coexisting features of self-consistency and limitations. At a practical level, this suggests that for both human thinking and artificial intelligence, to achieve continuous, paradigm-shifting innovation, we must face the bottlenecks of cognitive structures and, when necessary, seek changes that transcend the existing framework (such as introducing meta-cognition or open systems). Future research can further formally verify certain propositions on this basis (such as the conditions for determining non-generatable semantics), or try to apply the strategies proposed in this paper to the design of artificial intelligence systems to observe the actual performance of innovation output in a closed environment.

In conclusion, the DIKWP × DIKWP model provides a new perspective for understanding the relationship between cognition and innovation: innovation is both a product of tensor transformations within a closed system and a process that drives the system's evolution and pushes it towards its limits. The exploration of these limits, in turn, guides us in the direction of breaking through them. In today's era of continuous development of complex intelligence, such theoretical thinking is undoubtedly of great inspirational significance.

References:

1.Schematic structure of the DIKWP mesh cognitive model (five layers of... | Download Scientific Diagram, https://www.researchgate.net/figure/Schematic-structure-of-the-DIKWP-mesh-cognitive-model-five-layers-of-data-D-information_fig1_391731881

2.Applied Sciences | Special Issue : Purpose-Driven Data–Information–Knowledge–Wisdom (DIKWP)-Based Artificial General Intelligence Models and Applications, https://www.mdpi.com/journal/applsci/special_issues/SRBD8537AB

人工意识与人类意识

人工意识日记

玩透DeepSeek：认知解构+技术解析+实践落地

人工意识概论：以DIKWP模型剖析智能差异，借“BUG”理论揭示意识局限

人工智能通识 2025新版 段玉聪 朱绵茂 编著 党建读物出版社

主动医学概论 初级版

主动医学 ：人工智能赋能人类健康

世界人工意识大会主席 | 段玉聪

邮箱|duanyucong@hotmail.com

世界人工意识科学院

邮箱 | contact@waac.ac