很多时候我们都需要在不确定的环境中解决问题、制定方案、选择策略,小到个人生活的选择,大到企业和国家的策略选择,比如:
1、厂商推出向市场推出新产品时,潜在的顾客会做什么反应?应该生产多少的产品能够效益最大化?需要怎样的市场推广和广告投放来实现最优的费效比?
2、一家金融公司投资有价证券,哪些市场板块和单个有价证券前景最好?未来的盈利空间和走势会是怎么样?利率会如何变化?这些因素如何影响投资决策?
3、一个工程承包商投标一个合同,工程的实际成本是多少?有哪些公司会参与投标,其出价情况怎么样?
等等类似的商业问题都需要在不确定中确定策略、方案。下面就以一家石油开采为例,来说明在决策中是如何利用已有的条件来解决不确定的问题,并且如何获取有价值的信息来完善已有信息的不足,会容纳贝叶斯、决策树、敏感性分析、效用理论等知识,所有的实现都基于excel来完成的。
高富公司是一家石油钻探公司,该公司的主营业务就是在未经证实存在石油的地区购买地块并且钻探石油。公司CEO马斯克最近投入了几乎所有的运营资金在靠近大油田附近的地区购买了多块地块,主要原因是得到了地质学家的消息:这块地有四分之一的概率有石油。
马斯克经过计算,在这块地上钻探石油需要投入10万元,如果这地块是干涸的,这部分的投资将会全部损失,如果地块存在石油,将会为公司带来80万元的收入,公司获得70万元的利润。
此外,马斯克还有另外一个选择,另外一家大型石油公司知道了地质学家的报告,决定以9万元来购买这块地,最终承担1万的损失对债台高筑的马斯克来说还是很有诱惑力。
下图总结了不同的决策以及马斯克面临的可能的权衡:

马斯克目前的决策信息只有以上这么多内容,于是他就去咨询了一位商业分析师詹姆士,他们现在开始商业对话了。
詹姆斯:你认为咨询地质学家关于这块地有1/4的概率产石油的估计有多大的可信度?
马克斯:可信度不大,概率可能是1/3,或者是1/5。实际上他们自己并不知道。
詹姆斯:是否有途径能获得更多的信息来降低不确定性?
马克斯:有的。可以安排在这块土地上进行详细的地震勘探。但是不会真的发现是否有石油,除非你进行钻探。而且这些地震勘探花费巨大,需要30000元!如果进行钻探,可能什么也找不到,又要损失100000元!
詹姆斯:好。先把地震勘探放在一边。从简单的开始,下面可以选择你认为合适的准则,看一看是否值得进行地震勘探。如果值得,如何以最佳的方式使用这些信息。在此之后,要仔细分析这个问题,包括使用效用。
1、使用建立损益表模型
当对问题进行系统描述时,明确所有的相关方案及可能的自然状态是非常重要的,接下来就是要估计每一种决策方案和自然状态组合的收益,这就是损益表,下图是高富公司关于上述问题的损益表(单位:千元):

2、选择适合的决策准则
当决策是钻探石油还是出售土地时应该采用什么决策准则呢?对于这个问题并没有唯一的正确答案适合于每一个决策者。决策准则的选取主要取决于决策者自己的性格和对决策的态度,以及制定决策的环境。马克斯作为高富公司的所有人,需要最终决定哪一个决策准则最适合他自己的处境。
(1)不使用概率的准则:乐观准则
乐观准则,它提供了一个最好的可能结果(在整个损益表中最大的收益)出现的机会,如下图。

在右面多出的一列给出了每个备选方案的最大收益。既然这些备择方案的最大收益中的最大者必定是整个损益表中的最大收益,那么相应的备择方案(钻探石油)也就被这个标准所选择。
这个准则最大的缺陷是它完全忽视了先验概率。例如,它会始终认为高富公司应该钻探石油,即使发现石油的机会微乎其微。另一个缺陷是它忽视了除最大收益外其他所有的收益。例如,即使出售这块土地的收益是699(699000元),它仍然会认为高富公司应该钻探石油。
(2)不使用概率的准则:悲观准则。
悲观准则,关注可能发生的最差的情况,如下图

最右边的那列数字是所在行的最小值而不是最大值。因为90是这两个数字中最大的一个,所以被选定的备择方案是出售土地。
(3)使用概率的准则:最大可能性准则。
最大可能准则,建立在最有可能发生的自然状态的假设之上,有下面2个步骤:
(1) 发现先验概率最大的自然状态。
(2)选择在这种自然状态下收益最大的备择方案.
如下图。

上表和前面给出的损益表完全相同,但该表标明了此准则应用的第一步(选取干涸的自然状态)和第二步(选取出售土地这个备择方案)。因为干涸是具有较大先验概率的自然状态,所以我们只考虑干涸这一列的收益(-100和90)。这两个收益中较大的一个是90,所以我们选择相应的备择方案,即出售土地。
(4)使用概率的决策制定:贝叶斯决策规则
贝叶斯决策规则直接使用可能自然状态的先验概率:
(1)对于每一种备择方案,将每一个收益乘以相应自然状态的先验概率,再把乘积相加就得到了收益的加权平均。在统计上,这一加权平均称为这个备择方案的期望收益。
(2)贝叶斯决策规则选择具有最大期望收益的备择方案。
下图显示了将这个准则应用于高富公司问题,B列、C列和D列显示了上图给出的损益表。单元格F5和F6通过利用输人到这些单元格中的公式执行了程序的第一步,即:
F5=SUMPRODUCT(Prior Probabilty,Drill Payoff)
F6=SUMPRODUCT(Prior Probability,Sell Payoff)
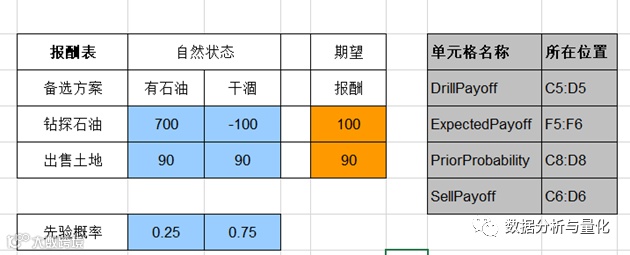
由于钻探的期望收益=100(单元格F5),与出售这块土地的收益=90(单元格F6)相比,这个准则建议进行钻探。
同其他方法一样,这个准则不能保证所选择的方案在实际情况发生时会成为最佳方案,
但它提供了另一个保证,如下所述:
“特定备择方案的期望收益可以被描述为在相同的情况下重复足够多的次数所出现的平均收益。因此,从平均的角度来说,重复使用贝叶斯决策规则制定决策会比其他准则带来更大的长期收益(假设先验概率是正确的)。”
因此,如果高富公司拥有许多具有相同损益表的土地,则在所有的土地上钻探石油会带来大约100的收益,而不是出售这些土地得到90的收益。下面的计算表明,在每四块土地中有一块有石油(就像先验概率所表明的那样)的情况下进行钻探所带来的平均收益为:
在一块土地上发现石油:收益=700,三块土地是干涸:收益=3(-100)=-300,总收益=400,平均收益=400/4=100。
詹姆斯:现在你要决定在目前情况下哪一个准则最适合你。
马克斯:我对任何一个准则都不是很满意。但好像这个准则广为应用。
詹姆斯:是的。
马克斯:为什么?
詹姆斯:有两个原因。首先,这是一个使用所有可用信息的准则。先验概率可能不像我们期望的那样准确,但它们大致让我们知道了每一种可能的自然状态出现的概率。
马克斯:我不同意这个看法。第二个原因是什么?
詹姆斯:记得,这个准则关注的是,如果相同的状况重复多次,那么平均收益是多少?我们称之为期望收益。从长期来看连续选择最佳期望收益的备择方案能够使得公司获得最多的收益。选择最有利于长期发展的决策对于管理人员来说是一个理性的决策。
2、使用决策树决策
上述方法采用了贝叶斯决策规则进行决策分析的方法,另一种采用此规则的启发性的方法是利用决策树以图形的方式表示和分析这个问题。
首先,需要制定的决策是在这块地上钻探还是出售这块土地。如果决策是进行钻探,下一个事件是了解这块土地下面是否有石油。最后获得收益。
在决策树术语中, 交汇点称为节点, 从节点发出的线称为树枝。节点有两种类型:决策节点用方块表示,表明在这一点上需要进行决策。事件节点用圆圈表示, 表明在这一点上会发生随机事件,树枝上括号中的数字给出了这个事件发生的概率。
我们根据高富公司的实际情况,使用excel创建如下的决策树:

在构建决策树的每一个步骤中, Excel使用贝叶斯决策规则自动完成决策树最佳策略的求解。每个决策节点内的数字表示哪一条树枝应该被选取(假设从那个节点出发的树枝按从上到下的顺序编号)。这样,对于上图中最终的决策树来说,单元格B9中的数字1表明第一条树枝(钻探备择方案)应该被选取。每一个结束节点两边的数字是到达那个节点时的收益。单元格A10和E6中的数字100是所在步骤的期望收益(贝叶斯决策规则绩效的度量指标)。
马克斯:决策树把一切都变得很透明。但是仍然有一个问题困扰着我。
马克斯:我巳经很清楚地表示了我不想将我的决策建立在咨询地质学家的数据基础上。有石油的概率是1/4,这仅仅是基于经验的猜测。
詹姆斯:好,让我来看看这一点。在决定钻探石油还是出售土地时什么是关键因素?
马克斯:那里有石油的可能性有多大。
詹姆斯:难道咨询地质学家不能帮助确定这一点吗?
马克斯:当然可以。没有他提供的信息,我不可能进行钻探。
詹姆斯:那么用于决定是否进行钻探的准则难道不应该直接基于这些信息吗?
马克斯:当然应该。
詹姆斯:但是我不明白你为什么一直拒绝使用咨询地质学家的数据。
马克斯:我没有拒绝使用他的信息。这些信息对于决策极其重要。我所拒绝的是将1/4的出油概率作为绝对真理使用,而这似乎就是贝叶斯决策规则要做的。如果他的数据与其实概率有出入,会发生什么情况。
詹姆斯:我明白了。如果不是25%,那么会低多少或高多少呢?
马克斯:我通常在咨询地质学家所说的基础上加减10%。因此我估计这个概率是介于15%到35%之间的某个值。
詹姆斯:好的。有一种管理科学技术可以用来处理这类情况,它被称为敏感性分析。它能够让我们研究如果咨询地质学家的数据偏离正确值时会发生什么情况。
3、使用决策树的敏感性分析
上面使用的概率1/4是地质学家给出的粗略估计,实际上,对于实际应用来说,通常都会在这个数字上+-10%,因此会介于15%-35%之间.
决策树中两个先验概率的和必须等于1,因此一个概率的上升会自动使得另一个概率以相同的数量下降,反过来也是如此。这在下图所示中的决策树中被单元格H6中的一个公式所执行,即干涸的概率=H 6=1-Probability OfOil(E22) 。上面的结论:在这块土地上有石油的真实概率在15%~35%之间。换句话说,有石油的真实先验概率在0.15~0.35之间,因此相应的土地干涸的概率在0.85~0.65之间。
一次是先验概率的下限(0.15),另一次是上限(0.35)。当有石油的先验概率只有0.15时,由于收入差额很大,因此决策变为出售土地(期望收益为90,钻探仅为20)。然而,当这个概率为0.35时,收入差额使决策变为钻探(期望收益=180,出售土地仅为90)。因此,决策对于有石油的先验概率非常敏感。这个敏感性分析表明,如果可能的话,很有必
要再多进行一些工作来找出有石油的真实概率是多少。


上图说明了最优行动过程从出售土地转向钻探石油的条件是有石油的先验概率为0.23和0.25之间的某个值。用代数方法可以找出这个先验概率的确切值,如下所示:
设p=有石油的先验概率。对于钻探石油的备择方案:
期望收益=p(700)+(1-p)(-100)=800p-100
设期望收益=90(卖出土地的收益),即800p-100=90,得到p=0.2375。
最终得到的结论是,当p<0.2375时应该出售土地,当p>0.2375时,应当进行钻探。
马克斯:当有石油的概率低于23. 75%时,我应该出售这块地。如果概率大一点,我就该进行钻探。它证实了我一直怀疑的事情。这是一个很好的决策依据,它完全取决于选择适当的有石油的概率。我希望除了咨询地质学家的数据外我能够得到更多的信息。
詹姆斯:前面你谈到过花3万元进行细致的地震勘探的可能性。
马克斯:是的,我可能会那样做。但是3万元!我仍然不能肯定这是否值得。
詹姆斯:我有一个快捷的方法来解决这个问题。这种方法被称为全情报价值。全情报价值是指如果地震勘探能够很肯定地告诉你那里是否有石油的话,你所得到的期望收益的增加量。
马克斯:但是地震勘探不能肯定地告诉你。
詹姆斯:是的,我知道。找出那里是否确实有石油就是我们所说的全情报。因此,你得到的确实信息所带来的期望收益的增加值就是全情报价值。这个信息要好于实际进行地勘探所提供的信息。
马克斯:没错。
詹姆斯:好,假设我们发现全情报价值低于3万元。由于全情报比我们进行地震勘探得到的信息要好,因此这就明确告诉我们不值得进行地震勘探。
马克斯:我懂了。但是如果全情报价值高于3万元呢?
詹姆斯:这时你就无法知道是否值得进行地震勘探,除非你进行进一步的分析。这个分析将会花费一些时间,但是它能够很快速计算出全情报价值。检查一下全情报价值是否低于3万元是很值得的,这将会节省大量的工作。
4、根据全情报价值来决策分析
前文决策所用的依据都是依赖于已知的先验条件,那么如果能够获得新的决策信息对于科学决策肯定是有很大帮助的,但是这需要考虑获取信息的成本问题。对于马斯克来说,衡量的标准是用实际勘探相同数量的钱找出真实的自然状态,然后决定是否值得为这些信息花钱。马斯克认为只要获取信息的价值在勘探成本3万元以内,这些信息就是有价值的,进行这种分析的关键数量为:
EP(无更多信息)=根据原始的先验概率通过贝叶斯决策规则得到的期望收益=100。
EP(拥有全情报)=知道真实的自然状态后制定决策得到的期望收益,EVPI=全情报价值,C=获取更多信息的成本,=30(进行地震勘探的成本,单位:千元)
全情报价值计算为:
EVP I=EP(拥有全情报) -EP(无更多信息)
在计算出EP(拥有全情报) 和EVP I后, 最后一步是比较EVPI和C:
如果C>EVP I, 则不值得获取更多的信息。
如果C≤VPI, 则值得获取更多的信息。
最终的结果是下表所示:

最终得到EVPI=142.5>30也就是说如果地震勘探可以明确表明那里是否有石油,进行勘探可以使得平均收益增大142500元,扣除3万元的成本,还可以得到112500元。
因此,是值得进行勘探开发的。
马克斯:你是在告诉我,如果地震勘探可以明确表明那里有石油的话,进行这样的勘探可以使平均收益增加大约142500元。
詹姆斯:是的。
马克斯:可以得到112500元。地震勘探并不令人如意。
詹姆斯:假设那里有石油,得到期望的地震探测回波的次数是多少?
马克斯:大约是60% 。
詹姆斯:现在假设土地是干涸的。你仍然得到期望的地震探测回波的次数是多少?
马克斯:很多!地震勘探告诉我那里有石油而实际上什么也没有。这就是为什么不愿意花30000元的原因。
詹姆斯:是的。这就是说在接近一半的时候它告诉你应该钻探,而实际上你不应该进行钻探?
马克斯:没有那么严重但经常如此。
詹姆斯:能给我一个百分比吗?
马克斯:大约20%。
詹姆斯:好。我想现在我们可以为是否值得进行地震勘探的决策做一些分析了。
马克斯:你将如何进行分析?
詹姆斯:我们将在出现希望的地震探测回波的情况下,计算有石油的概率到底是多少,然后在没有出现希望的地震回波的情况下再计算这个概率。我们将咨询地质学家提供的数据称为先验概率,它们是在得到更多的信思之前获得的。经过改进的数据称为后验概率。
马克斯:好的。
詹姆斯:如果我们进行地震勘探,在减去3万元的费用后,我们用后验概率来计算平均收益。如果这个收益大于不进行地震勘探的收益,我们就应当进行地震勘探。反之就不要进行。
未完待续......


