编者按:
在我刚入行时, 就经常听栾生老师的大名, 也听过栾老师讲述的课程, 很早就关注栾老师的博客, 里面有很多好文章, 以后给大家逐篇介绍.
这篇是孪老师的博客上所写, 主要是讨论了全基因组选择中G矩阵的构建流程. 我们知道基因组选择中的核心是利用SNP信息, 构建G矩阵来描述个体间的亲缘关系, 根据的是IBS, 是更广泛意义的相似. 根据SNP构建的G矩阵反应的是个体现实关系矩阵(Realized Relationship Matrix), 而系谱构建的矩阵会有孟德尔抽样误差.
阅读文章内容, 感觉很有亲切感, 作者的所思所感跃然纸上, 正所谓文如其人. 以下为博客内容:
如何构建G矩阵-基因组亲缘关系矩阵(Genomic relationships matrix)
自己的选择育种知识,又到了大规模系统学习和更新的时候了。
自从2005年开始学习水产动物选择育种知识以来,采取囫囵吞枣模式,虽然对于REML算法和BLUP算法的细节知识仍然一知半解,好歹相关的软件如ASReml、R等可以以较为熟练的使用,对于选择育种体系的理解也逐渐深入,常规的遗传评估工作算是可以胜任。
全基因组选择方法建立以来,尽管迅速在奶牛、猪等大动物上展现了优越的性能,然而对于虾等个体小、世代周期短的动物,如何应用,仍然是一个难题,也是我正在努力研究的方向。
然而,基于高通量SNP标记信息,获得的亲缘关系更加准确,这一结论已经毋容置疑。
因此,自这个blog开始,将逐渐学习、并记录基于SNP标记的基因组选择评估方法,逐渐更新自己的知识体系。随着年龄的增大,知识体系的更新会慢很多,且行且记吧。
计算G矩阵的方法有很多种,目前引用较多的是Vanraden于2008年发表在JournalofDairyScience上的文章“”中所建立的方法,目前该论文已经被引用了超过1500次。
一些背景知识:
IBD(Identicalbydiscent),血缘同源。
IBS(Identicalbystate),状态同源。
通常我们会讲,如果一段DNA在两个或者多个个体中均有一致的核苷酸序列,那么可以定义该DNA片段属性为状态同源,即IBS。
在两个或者多个个体中的一个IBS片段,如果遗传自一个共同的祖先个体,且没有发生重组,那么该片段也是血缘同源的,即IBD。
一段DNA片段,如果是IBD,那么肯定也是IBS;如果片段不是IBD,也有可能是IBS,因为不同个体中发生了相同的突变,或者重组没有改变片段等原因所致。
关于IBD和IBS的定义,参见Wiki。
个体间的亲缘关系,可以通过以下两种方法估计:
通过系谱进行计算,利用处于IBD状态的等位基因估计个体间的亲缘关系
通过分子标记,利用处于IBS状态的基因估计个体间共享染色体片段的百分比,估计个体间的相似性
下边的SNP例子,主要来自FikretIsik的一个Presentation:https://articles.extension.org/pages/68019/genomic-relationships-and-gblup,但幻灯片中P、Z矩阵的计算结果是错误的。
1.构建M矩阵
M矩阵是一个n×m矩阵,n表示个体数(the number of individuals),m表示位点数(the number of loci)。
譬如有3个二倍体个体,4个SNP位点。对于每个位点,小写等位基因表示其出现频率最低。
rm(list=ls())
# 加载synbreed包
is_installed <- require(xtable)
if (!is_installed) {
install.packages("xtable")
library(xtable)
}
genotypes <-
data.frame(
snp1 = c("AA", "AA", "tt"),
snp2 = c("Ct", "Ct", "CC"),
snp3 = c("GG", "Ga", "GG"),
snp4 = c("Ag", "AA", "AA"),
row.names = c("Ind1", "Ind2", "Ind3"),
stringsAsFactors = FALSE
)
print(xtable(genotypes),type="html")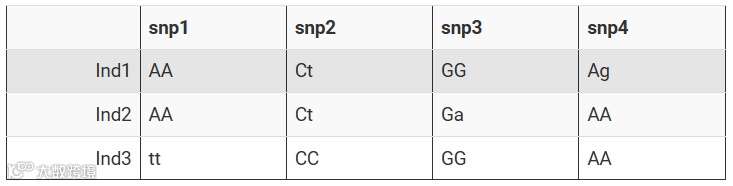
把基因型矩阵转换为基因含量矩阵,具体参数用基因型中最小频率等位基因的个数表示,即0、1、2。因此我们称这个矩阵为MAF矩阵。
转换用到了synbreed包中的codeGeno函数。
# 加载synbreed包
is_installed <- require(synbreed)
## 载入需要的程辑包:synbreed
if (!is_installed) {
install.packages("synbreed")
library(synbreed)
}
# 把小写字母转换为大写字母
genotypes <- apply(genotypes, 2, function(x) toupper(x))
# 创建codeGeno函数需要的数据类型
genotypes_gp <- create.gpData(geno = genotypes)
# codeGeno默认计算MAF等位基因的个数
M <- codeGeno(genotypes_gp,reference.allele = "minor")$geno
M
为了便于计算,通常会将M矩阵减1,每个位点等位基因含量变为-1、0、1三种形式。
M <- M - 1
M
2.MM’矩阵
M %*% t(M)
MM’对角线数字为2、2、4,分别表示三个个体基因型为纯合的位点数。譬如Ind1,四个位点中有两个位点的基因型为纯合类型(AA和GG),而Ind3个体四个位点基因型全部为纯合类型。
非对角线元素,表示亲缘个体间共享的等位基因数。原英文:off-diagonals measure the number of alleles shared by relatives,不是很理解。
3.M’M矩阵
t(M) %*% M
M’M对角线数字为3、-1、0、0,分别表示四个位点纯合基因型的个体数。譬如位点snp1,有3个个体基因型全部为纯合;位点snp2,有1个个体基因型为纯合。
非对角线元素表示什么意思,还不是很清楚。
off-diagonals measure the number of times alleles at different loci were inherited by the same individual.
4.构建P矩阵
根据下述公式构建P矩阵的每一列:

其中i表示位点编号,pi表示每个位点最小等位基因频率。
#计算每个位点的MAF.
p_lower <- (apply(M,2,sum)+nrow(M))/(nrow(M)*2)
p_upper <- 2*(p_lower-0.5)
p_matrix <- matrix(p_upper,byrow=T,nrow=nrow(M),ncol=ncol(M))
P <- p_matrix
P
每一列,及每个位点的等位基因频率都是相同的数字。
5.构建Z矩阵
Z矩阵实际上是中心化后的M矩阵。
Sets means values of the allele effects to 0. 从下边Z矩阵可以看出,每一列SNP位点,等位基因效应的和为0。
Gives more credit to rare alleles than to common alleles when calculating genomic relationships. 意思是以MAF基因频率去进行中心化?
Allele frequencies in P should be from the unselected base population rather than those that occur after selection or inbreeding. An earlier or later base population can lead to greater or fewer relationships and to more or less inbreeding.
The genomic inbreeding coefficient is greater if the individual is homozygous for rare alleles than if homozygous for common alleles.
Z <- M - P
Z
6.构建G矩阵
构建方法,在文章中提到了3种:
6.1第一种方法:

Z为SNP标记的设计矩阵;公式中,pi为每个位点的最小等位基因频率。公式中分母部分,是为了使G矩阵与A矩阵的尺度相一致。scales G to be analogous to the numerator relationship matrix A.
d <- 2*sum(p_lower*(1 - p_lower))
G <- Z %*% t(Z) / d
print(xtable(G),type="html")邓飞在他的科学网,利用sommer包对上述结果进行了验证。在此,同样利用sommer包的函数进行验证。可以看出,结算结果是一致的。sommer包现在核心函数已经用C++重写,性能可期待。
suppressPackageStartupMessages(is_installed <- require(sommer))
if (!is_installed) {
install.packages("sommer")
library(sommer)
}
print(xtable(A.mat(M)),type="html")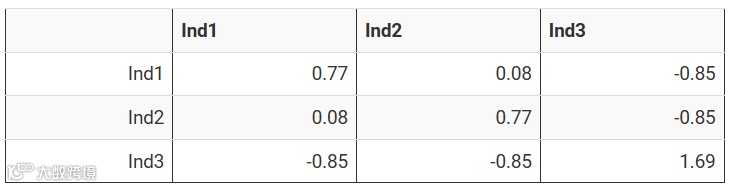
个体j的基因组近交系数等于Gjj-1。
diag(G) - 1
前两个个体的近交系数为负值,基因组近交系数跟传统的基于系谱的近交系数并不在一个尺度上。
个体间的基因组亲缘关系,譬如j、k个体间的亲缘关系,等于
现在计算Ind1和Ind2个体间的亲缘关系,等于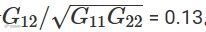
6.2第二种方法

D是一个对角矩阵,其中Djj等于
第二种方法是第一种方法的一个变体,利用每个位点期望方差的倒数,对标记效应值进行加权。
D_ii <- 1/(ncol(M)*(2*p_lower*(1 - p_lower)))
# 构建对角矩阵
D <- diag(D_ii,ncol(M))
G <- Z %*% D %*% t(Z)
print(xtable(G),type="html")参考文献:
Vanraden P M. Efficient methods to compute genomic predictions.[J]. Journal of Dairy Science, 2008, 91(11):4414-4423.
阅读原文提示链接不能使用, 因此将栾老师博客地址贴在这里: https://luansheng.netlify.com/post/how-to-construct-g-matrix/
如何使用RStudio的blogdown并利用github通过netlify搭建自己的博客



