内容提要:
* 因何而“朴素”
* 后验概率最大化准则
点击蓝字 |关注我们
欢迎回来。在上篇推送中,我们给大家介绍了朴素贝叶斯法,我们常用它解决分类问题,所以就有了朴素贝叶斯分类器,从根本上来说它就是一种「分类方法」。从起名就看得出来,它将「贝叶斯定理」、「特征条件独立假设」两者结合在一起。

今天我们继续说说,朴素贝叶斯「因何而朴素」,它的判断准则又是什么呢?
壹 如何理解“朴素”
首先,来看一个训练数据集,计算得出一个联合概率分布。
❝已知训练数据集:
❞
「输入」: ,
「输出」: ,
生成方法:学习联合概率分布
还记得在第一章中,我们给大家介绍了生成方法和判别方法。区别在哪呢?
「1.生成方法:」 首先学习联合概率分布 ,得到条件概率分布 ,即生成模型,比如朴素贝叶斯法和隐马尔可夫模型。
「2.判别方法:」 直接从训练数据集得到决策函数 或者条件概率分布 作为预测的模型,比如 近邻法、感知机、逻辑斯谛回归模型、最大熵模型、支持向量机等。
接下来,我们就一起看如何求出联合概率分布。
1. 联合概率分布
还是以巧克力为例。
❝请问:巧克力是黑色的并且来自于 盒的概率 是多少?
❞
这里的 其实就是联合概率分布
-
「 」 对应的是颜色特征 -
「 」 对应的是所属类别
根据上篇讲义【十分钟 机器学习 系列课程】讲义(十五):朴素贝叶斯定理,我们可以快速地列出这个求解公式:
叫做「先验概率分布」,也可以表示成:
叫做「条件概率分布」,也可以表示成:
这样是不是很容易理解呢?接着,就可以对巧克力的每个「特征(颜色)」 计算出联合概率分布。

没错,这里的条件发生了对调,由 变成了 。
这一个,就称为「后验概率分布」。
再一次体现出贝叶斯思维就是条件概率的「逆向」思维。
那么为什么要「朴素」呢?
2. 为什么要有条件独立性假设?
上篇推文中,我们讲到:
❝朴素:特征条件相互独立❞
举个栗子。
看过日漫的小伙伴,都知道有很多的帅哥,那么帅是怎么定义的呢?
你喜欢哪个类型的呢?是黑执事中的塞巴斯蒂安,还是夏目?这时候我们可以简单的取四种特征,来做个判断,在你心目中到底谁更帅。
此时,可以根据特征列一个表格:
| 特征 | 种类 | 种类 |
|---|---|---|
| 身高 | 高于170cm -高 | 小于等于170cm-矮 |
| 体重 | 高于70kg-重 | 小于等于70kg-轻 |
| 脸型 | 圆脸 | 长脸 |
| 鼻型 | 高鼻梁 | 低鼻梁 |
假如每种特征都有两种情况,并且最后的属性也有两种,那么计算联合概率分布时,会有 种组合。
如果用数学语言表达就是:
1.「 的可能取值有 个」组合数就是
2.「 的可能取值有 个」
3.「总的组合数就是 」
惊人的组合数,随着指数级的增加而递增。
指数增长是非常恐怖的!
以新冠肺炎为例,假如现在感染的人数是
人,按照每天新增
的比例增加,那么到了第
天,感染的人数会增加到
,如果不加以控制,从
人到全球
亿人,理论上只需要
天。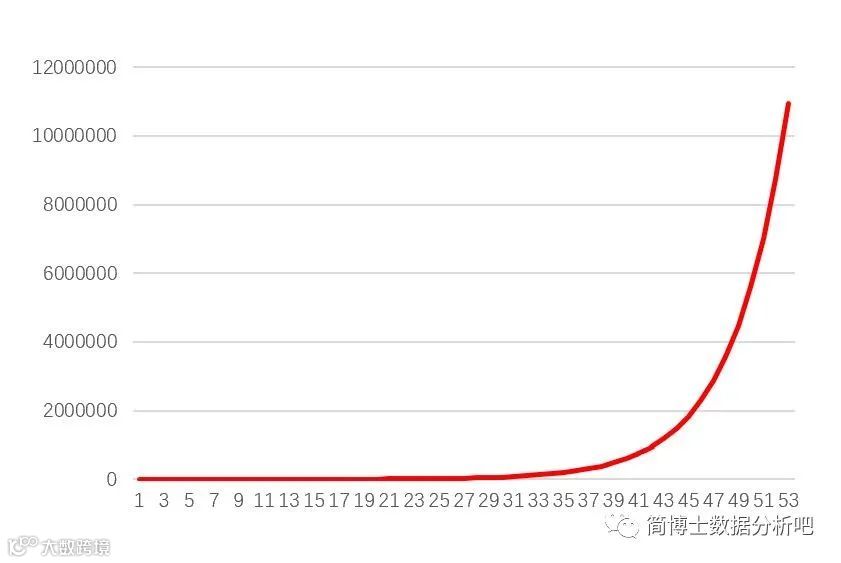
因此,在朴素贝叶斯法中,需要加了一个特征相互独立的假设,不然我们计算不出来这么大的联合概率分布,这样就可以转化为简单的形式:
于是,「后验概率」就是:
贰 后验概率最大化准则
1. 朴素贝叶斯分类方法
了解了朴素贝叶斯法的重要性,那么我们再来看看它的具体计算方法是什么?
❝假如存在 类 ,现在给定一个新的实例
问:该实例归属哪一类?❞
这个问题对我们来说并不陌生,在上篇推送中已经给出了答案。
由于分母都相同,因此,只需要计算出分子的最大值就可找出这个实例所对应的类。
2. 0-1损失函数
那么对应的判断准则又怎么界定呢?如果得到模型有多个,那个模型更好呢,如何进行比较?
0-1~损失函数
是分类决策函数
是对应的分类,输出空间为
当两者相等,证明分类正确,没有损失,反之记为1,有损失。
这个损失函数对应的期望是:
期望的下标 ,表示这里的期望对应的是已知 下 的条件概率分布。
学过概率论的小伙伴们都还记得:
❝数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一,它反映随机变量平均取值的大小。❞
于是,之前的式子可以写为:
而我们知道当 时,损失记为1,反之为0,没有损失,也就意味只有当 时,才会有损失值,否则都为0,这样就可以对这个函数进行简化:
注意:「由于在 的分类中,最终只有最小值满足 」
欢迎大家关注简博士的B站和公众号,在公众号私信“入群”,可以与小伙伴们一起讨论问题哦。

扫码关注我们
微信号|Dr_Janneil
B站|简博士


