

方差分析

数据分析和应用

2020-05-09

导读：我们在《一文学会t检验》中介绍了两样本均数比较的t检验，当需要进行多个样本均数间的比较时，则需要用到方差分析，今天我们为大家介绍的是完全随机设计的方差分析和随机区组设计的方差分析。

前面我们在《一文学会t检验》中介绍了两样本均数比较的t检验，当需要进行多个样本均数间的比较时，则需要用到方差分析（统计方法概括可见《医学常用统计分析方法概括》）。方差分析由英国统计学家Fisher所提出，它的基本思想是：把全部观察值间的变异按设计和需要分解成两个或多个组成部分，然后将各部分的变异与随机误差进行比较，以判断各部分的变异是否具有统计学意义。

方差分析需要满足3个条件：1.独立性: 各样本是相互独立的随机样本；2.正态性: 各样本来自正态总体；3.方差齐性: 各总体方差相等。今天为大家介绍如何通过R语言对完全随机设计资料和随机区组设计资料进行方差分析。

1 完全随机设计的方差分析

问题提出

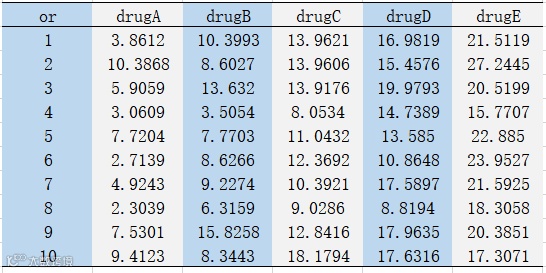
某临床实验中心想测试五种药物降低胆固醇的疗效，将50名参与者随机分成5组，每组分别接受一种药物，数据资料如表1所示，研究者想比较这五种药物的疗效有无显著差异。

表1 数据资料

数据准备

该研究的因变量为连续型变量，属于完全随机设计资料。在R语言中进行分析时，该数据资料需整理成表2的格式。在R语言中，我们可以使用以下代码，将其转化为图2的结构。

#改变数据结构#
a1<- read.csv("C:\\Users\\Lenovo1\\anov1.csv")
a2<-melt(a1,id.vars=c("or"),variable.name="trt",value.name="response")
#其中id.vars后面跟着依然保持在列上不变的量，而variable.name用于为新变量命名，value.name用于为值命名。#

表2 转化后的数据结构

整理好数据后，可以使用aggregate函数来了解数据的均值和标准差，对我们的数据有一个初步的认识（图1）。

#简单的统计描述#
aggregate(a2$response,by=list(a2$trt),FUN=mean) #各组的均值 
aggregate(a2$response,by=list(a2$trt),FUN=sd)#各组的标准差

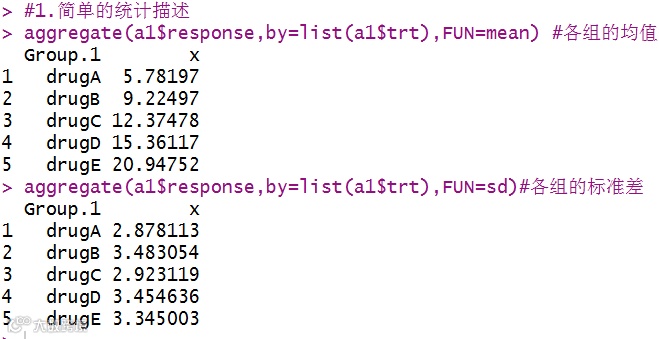
图1 描述统计结果

正态性检验和方差齐性检验

整理好数据后，我们需要先对数据资料的正态性与方差齐性进行检验，作为分析方法判定的依据。代码如下：

#(1)正态性检验
shapiro.test(a2$response)
library(car) 
qqPlot(lm(response ~ trt, data = a2))
#(2)方差齐性检验
bartlett.test(response~trt,data=a2)

本文使用了W检验法进行正态性检验，W值为0.97，接近于1，表明数据和正态分布拟合得好，更多正态性检验的方法可见推文《正态性检验》。

图2 正态性检验结果

bartlett检验是方差齐性检验的一种常用方法，当α=0.05，P值大于α值，我们接受原假设，可以认为总体方差是相等的。

图3 方差齐性检验结果

方差分析

根据上述结果，该研究数据资料符合正态分布，方差齐性，可使用完全随机设计资料的方差分析。分析代码如下：

aov <- aov(response ~ trt,data=a2) 
summary(aov)#提取方差分析的结果

图6显示了方差分析的结果，其中各项意义为，trt：处理组，Residuals ：误差项，Df：自由度，Sum Sq：离均差平方和，Mean Sq：均方，最下面一行Signif.code代表P值，后面跟着几个*号，P值就小于相对应*号后的那个数，例如图6中，当α=0.05，P值小于0.0001，P值小于α值，我们拒绝原假设，不能认为五个组的总体均数是相等的。

图4 完全随机设计资料的方差分析结果

2 随机区组设计的方差分析

随机区组设计又称为配伍组设计，是对配对设计的扩展，具体做法是：先按影响实验结果的非处理因素（如性别、年龄、体重、职业、病情等）将实验对象配成区组，再分别将各区组内的实验对象随机分配到各处理组或对照。

问题提出

某研究者想测试三种药物降低胆固醇的疗效，先按某种非处理因素将30名受试对象配成10个区组（group)，再分别让每个区组内3名受试者分别随机接受一种药物，研究三种药物的疗效有无显著差异。数据资料如表3。

表3 数据资料

数据准备

我们首先将数据结构整理成如表4，变量分别为区组(group)、处理因素(trt)和胆固醇下降值(response)

表4 随机区组资料方差分析的数据结构

方差分析

先做正态性检验和方差齐性检验，方法如上所述，此处不再具体赘述。检测数据资料符合正态和方差齐后，然后做方差分析，代码如下：

library(multcomp)
a3<- read.csv("C:\\Users\\anov.csv")
shapiro.test(a3$response)  #(1)正态性检验
library(car) 
qqPlot(lm(response ~ trt, data = a3))
bartlett.test(response~trt,data=a3)  #(2)方差齐性检验
###方差分析
a3$group<-as.factor(a3$group)
aov2<-aov(response ~ group+trt,data=a3)
summary(aov2)

其中要注意的是，我们需要将区组变量(group)改为因子型变量，因为区组变量(group)下都是数字1-9，如果不改为因子型变量，会导致R语言识别错误，最终影响结果中的自由度，也会导致结果错误。图9显示了不改为因子型的结果。图10显示了正确的结果。结果中会依次显示区组，处理组，误差的自由度，离均差平方和，均方，F值，P值。当α=0.05，P值小于α值，我们拒绝原假设，不能认为10个区组的总体均数是相等的，也不能认为3个处理组的总体均数是相等的。