由之前的文章我们可知,分布滞后非线性模型(DLNM)能够同时考虑暴露因素的滞后效应和暴露-反应的非线性关系,通常用于研究空气污染、气象等暴露因素的健康效应。该模型的核心思想就是建立一个包含暴露变量和滞后维度的交叉基,并将交叉基作为变量纳入模型中,达到同时分析暴露变量维度和滞后维度作用的目的。
实现DLNM主要依赖于R包“dlnm”,通过onebasis或crossbasis函数构建交叉基。onebasis和crossbasis区别在于:crossbasis可同时纳入不同的暴露值和不同的滞后值;onebasis通常只考虑暴露变量的转换。
一、交叉基建立的基本步骤

💜(1)自变量维度的基函数选择
基函数(basis function)是指将自变量转化为一个新的变量集,并将其包含在模型的设计矩阵中,从而对其效应进行估计的函数。我们常用的基函数包括正交函数、线性阈值函数和样条函数等,在常用的基函数中样条函数应用最广,样条函数是指是一类分段(片)光滑、并且在各段交接处也有一定光滑性的函数,由这样的样条形成的曲线在连接点处具有连续的坡度与曲率。常见的样条函数包括:样条平滑,自然三次样条,B样条等。基函数的基本应用公式如下:

Xt为暴露因素,如逐日温度、空气污染物浓度、湿度等环境因素。Zf为n×vx矩阵,是自变量x通过基函数f()转换产生的新变量,称基变量。通过转化后的自变量能更细致的描述其与因变量的变化关系,得出更精确的暴露反应关系。
由于暴露的影响存在滞后性,当天的结局最长可能受L天前暴露的影响。为了描述暴露的滞后效应,同样需要选择一个基函数对滞后进行转换形成矩阵。通常情况下,使用“bs”、“ns”或者“strata”等基函数对滞后维度进行设置时,其节点一般指定在对数刻度的等距值处。
💜(3)结合自变量维度的基函数和滞后维度的基函数,可得到自变量-滞后的交叉基函数。

💜(1)onebasis函数
在R中onebasis的具体用法为:onebasis(x, fun="ns", ...),其中x指的暴露变量;fun指的是基函数,默认为“ns”。在当前的“dlnm”包中,可供选择的基函数如下:
表1 基函数类型

在R中crossbasis 的具体用法为:crossbasis(x, lag, argvar=list(), arglag=list(), group=NULL, ...)。其中,X表示暴露变量,lag表示最大滞后天数,argvar表示暴露变量的设置参数列表,arglag表示滞后的设置参数列表,group为分组变量,…表示更多的参数设置。
三、实例分析

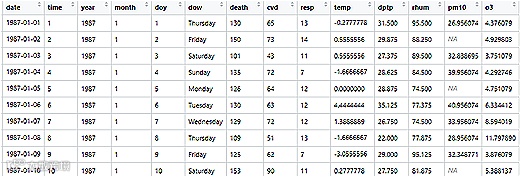
图1 芝加哥1987—2000年逐日死亡及气象数据
建立死亡与温度关系的交叉基的完整R代码如下:
##安装并加载dlnm包
install.packages("dlnm")
library(dlnm)
library(splines)
##读取数据集
data<-chicagoNMMAPS
##建立暴露反应关系维度的基函数,采用自然立方样条函数,节点位置设置在第10、75与90百分位数;
argvar<-list(fun="bs",degree=2,knots=quantile(data$temp,c(10,75,90)/100,na.rm=T))
##建立暴露滞后维度的基函数,根据经验滞后的自由度取4;节点位置设置采用程序包提供的对数等间距的方法
arglag<-list(fun="bs",df=4)
##建立暴露-滞后-反应的交叉基函数
cb<-crossbasis(data$temp,lag=21,argvar=argvar,arglag=arglag)
summary(cb)##查看交叉基矩阵的参数设置
> summary(cb)##查看交叉基矩阵的参数设置
CROSSBASIS FUNCTIONS
observations: 5114
range: -26.66667 to 33.33333
lag period: 0 21
total df: 20
BASIS FOR VAR:
fun: bs
knots: -3.888889 19.44444 23.88889
degree: 2
intercept: FALSE
Boundary.knots: -26.66667 33.33333
BASIS FOR LAG:
fun: bs
knots:
degree: 3
intercept: TRUE
Boundary.knots: 0 21
四、参考文献

[1] Gasparrini A, Armstrong B, Kenward M G. Distributed lag non-linear models[J]. Statistics in Medicine, 2010.
[2] Gasparrini A. Distributed Lag Linear and Non-Linear Models in R: The Package dlnm[J]. Journal of Statal Software, 2011, 43(8):1-20.
[3]杨军,欧春泉,丁研等.分布滞后非线性模型[J].中国卫生统计,2012,29(05):772-773+777.
制作:骆丽芳、周燕
初审:何冠豪、胡建雄
审核:肖建鹏、刘涛
指导:马文军

关于我们


邮箱:statisic@gdiph.org.cn
微信号:gdiph-stat


