前面讲解了使用蒙特卡罗方法 计算圆周率π 和 计算定积分,相信大家对蒙特卡罗方法有了大概的印象。总的来说,蒙特卡罗方法,就是通过模拟产生符合某个分布的随机数,把可能出现的数据模拟出来,然后通过这些数据去验证已有的模型。
在本篇文章里面,我会继续为大家介绍,如何通过蒙特卡罗方法,使用仿真模拟解决某种稀缺资源的排队使用问题。为了让文章通俗易懂,咱们来通过电影院观影后,公共厕所厕位的排队使用问题,来演示这类型问题的求解。
在日常生活中,电影院播放完电影后,因为电影的时长都是90分钟左右,看完电影,普通人肯定是想要上厕所的。因为厕所的资源是有限的,而观影之后上厕所的群众数量比较多,因此这个时间点上厕所,一般都是需要进行排队使用的。
如果电影院设置的厕所厕位太少,那么排队使用的人将会很多,这会给看电影的人带来非常不好的观影体验,可能下次就不买这个电影院的电影票了。如果电影院设置的厕所厕位太多,那么租借场地、清洁工人、设备维护等成本又太高,会照成资源的浪费。
这里,我们就来估计一下,在固定需求的前提下,我们通过调整厕位的数量,上厕所的顾客平均需要排队多长的时间,也就是排队上厕所的期望时长是多久。
为了简单起见,这里假设:
1、某个时间点电影结束之后,会有 n 个人想上厕所;
2、这 n 个人会在 m_fastest 到 m_slowest 秒钟之内全部到达厕所;
3、每个人上厕所时间在 d_fastest 到 d_slowest 秒钟之间;
4、厕所的位置总共有 r 个,每次只能一个人进行使用。
一般,厕所的使用流程图,如下图所示:
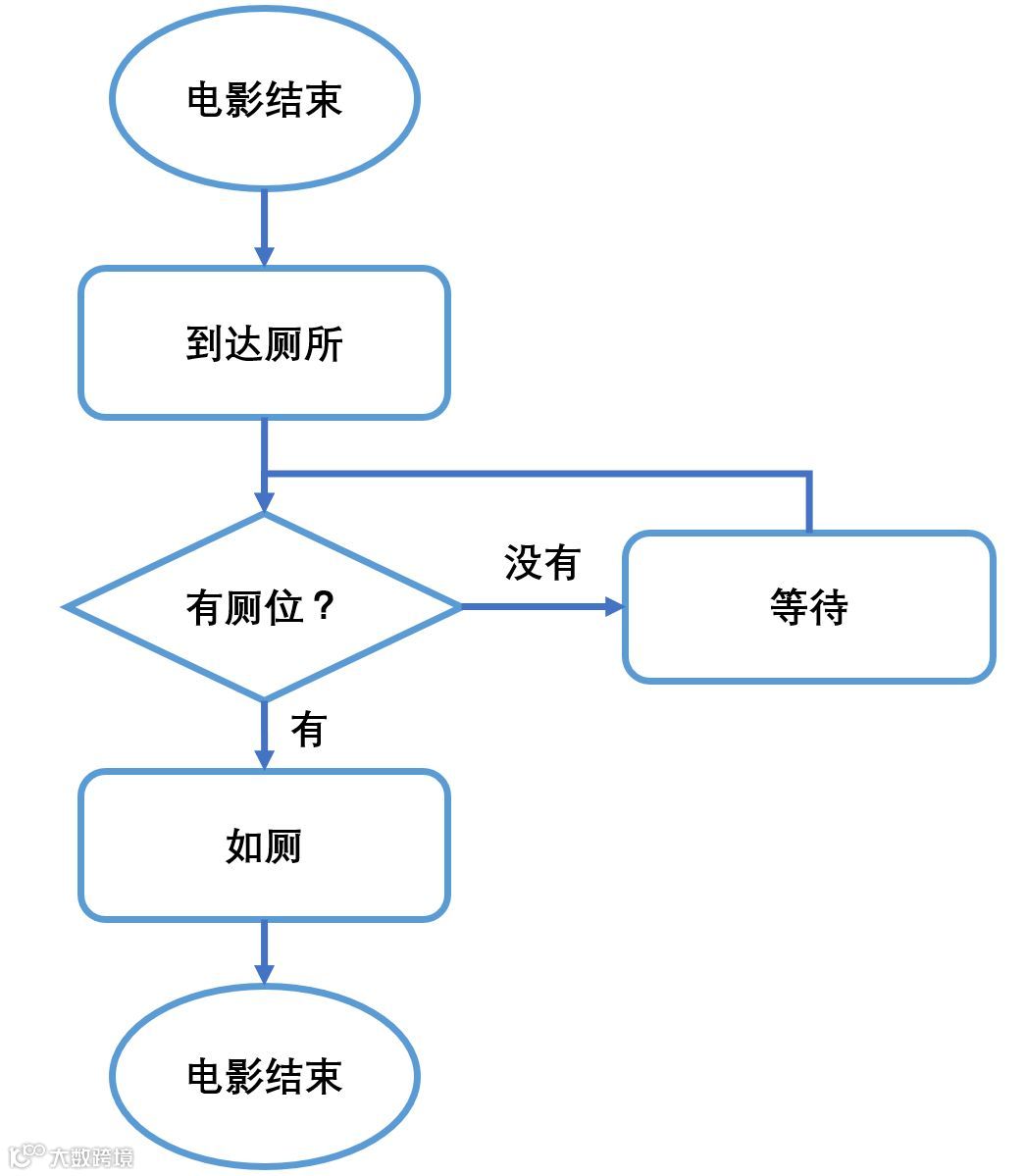
接着,需要模拟出每个人的以下数据:
1、到达时间
2、使用时长
接着,就可以开始实验了,先来假设:
1、n=30,也就是30个人会前后排队上厕所;
2、m_fastest=0,m_slowest=5*60,上厕所大军会在0到5分钟内抵达厕所;
3、d_fastest=1,d_slowest=2*60,每个人如厕需要1到2分钟的时间;
4、厕所位置 r,模拟有1个,2个,3个,4个,5个的情况。
当 r = 1 时:

先来介绍一下,这幅图怎么看。
首先是 x 轴,也就是横轴,就是时间,单位为秒,这个图中,处理完所有人的如厕需求,需要3000秒左右的时间。
然后是 y 轴,也就是纵轴,是具体某一个人,当厕所空闲的时候,值为 -1,也就是那个绿色的小点,第一个用户从0开始,以此类推,每个红色的直线,就是每个用户使用厕所的时长。
知道图片怎么看之后,我们可以看到,当 n=1,也就是只有一个厕位的时候,整个排队上厕所的时间,一直延续到3000秒,也就是50分钟,好可怕的时间,再来看看每个人需要等待的时长分布:

可以看到,平均等待时间,大约等于1250秒左右,憋尿这么长的时间,肯定是有害健康了,只有一个厕位的方案,肯定要被否认。
当 r = 2 时:

可以看到,整个排队上厕所的时间,一直延续到1400秒,也就是23分钟左右,这个时间也是非常可怕的,再来看看每个人需要等待的时长分布:

可以看到,平均等待时间,大约等于472秒左右,还是要憋8分钟左右的时间,感觉还是挺幸苦的。安排两个厕位的方案,也要被否认。
当 r = 3 时:

可以看到,整个排队上厕所的时间,一直延续到900以内,也就是15分钟左右,时间上,已经得到非常大的缓解,再来看看每个人需要等待的时长分布:

可以看到,平均等待时间,大约等于244秒左右,还是要憋4分钟左右的时间,感觉大家都可以忍受了。但是这个肯定带不来好的用户体验,还需要改进。
当 r = 4 时:

可以看到,整个排队上厕所的时间,一直延续到700以内,也就是12分钟左右,时间上,已经得到非常大的缓解,再来看看每个人需要等待的时长分布:

可以看到,平均等待时间,大约等于153秒左右,还是要憋2分钟左右的时间,感觉大家都可以忍受了。这个方案其实已经不错,基本上达到了资源的最优化配置,但是大家都知道,企业家都是有远见的,电影排片密集的时候,上厕所的人也会增加,为了适配这种特殊情况,我们继续增加厕位,看看体验如何。
当 r = 5 时:
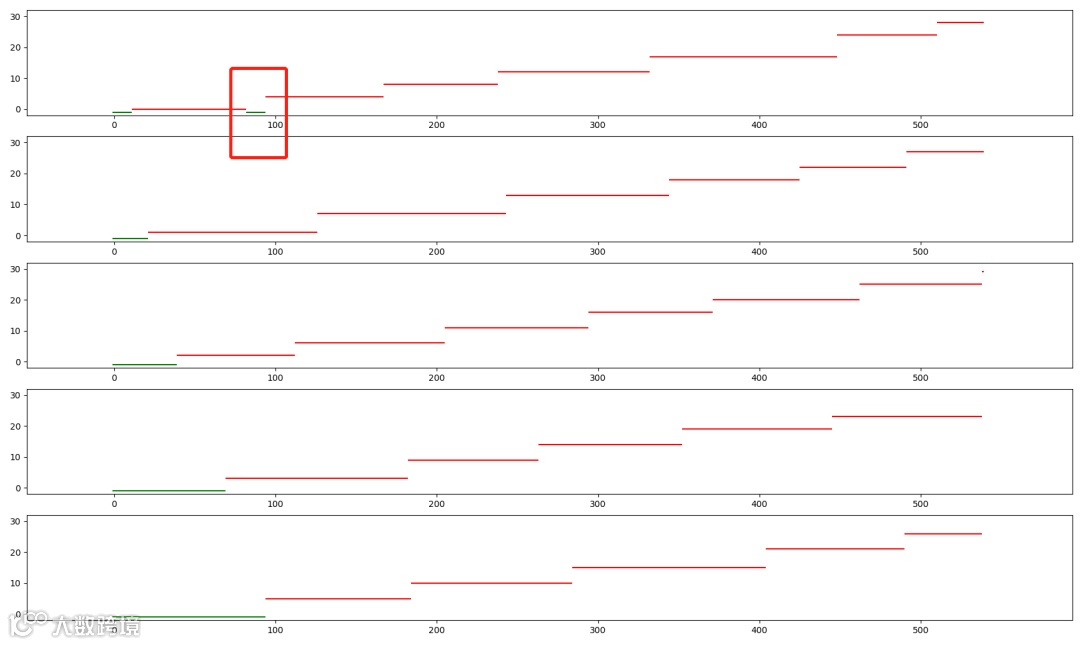
可以看到,整个排队上厕所的时间,一直延续到600以内,也就是10分钟左右,时间上,已经得到非常大的缓解,在第一个厕位100秒左右的时候,还出现了一个没人用的空挡(绿色的横线)。再来看看每个人需要等待的时长分布:
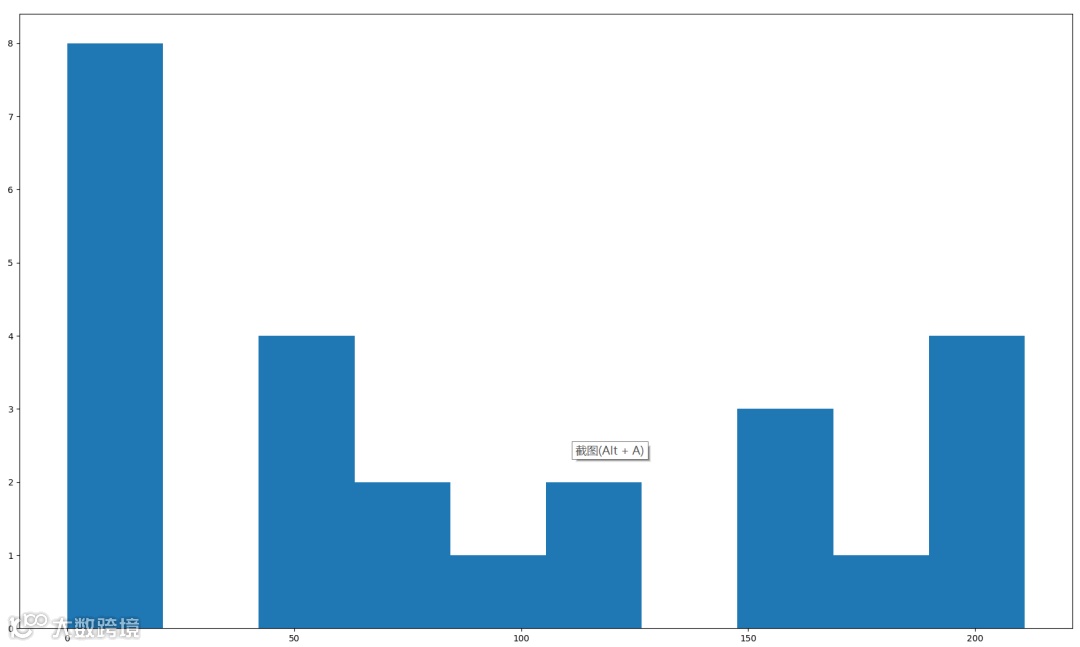
可以看到,平均等待时间,大约等于87秒左右,还是要憋1分钟左右的时间,感觉大家都可以忍受了。
当 r = 10 时:
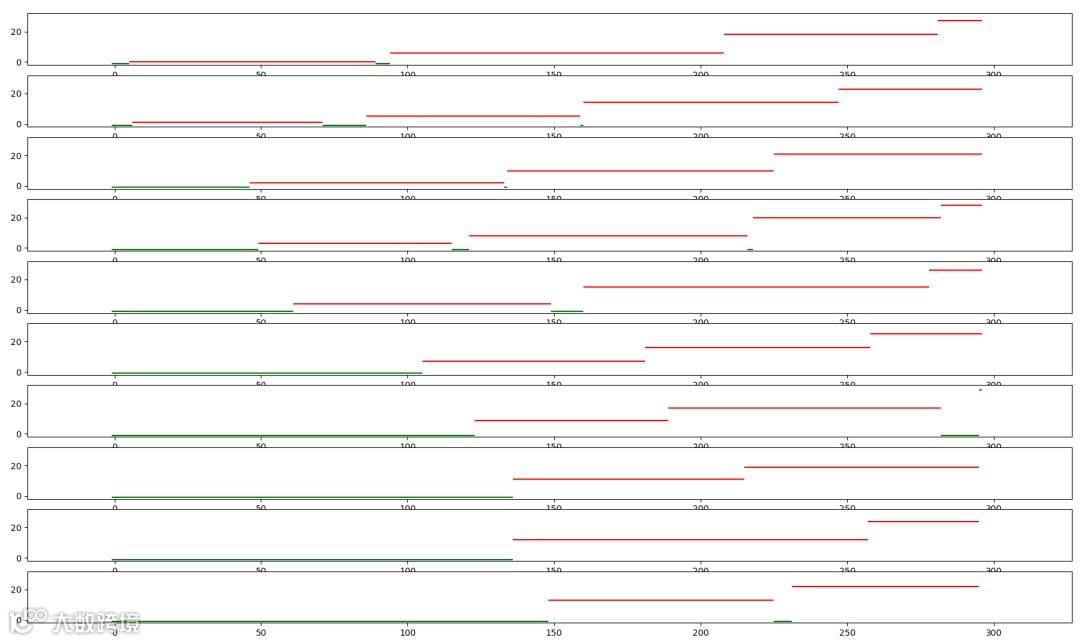
可以看到,整个排队上厕所的时间,一直延续到300以内,也就是5分钟左右,时间上,而且,很多厕位,出现了很长的时间都没有人用的情况(绿色的横线)。再来看看每个人需要等待的时长分布:

可以看到,基本上不需要怎么排队了,只有三个人需要排队,其他人都可以秒进了。
虽然我们使用了厕所排队这么一个浅显的案例,来介绍稀缺资源排队使用的仿真模拟问题,但是希望大家可以深入思考一下,这个场景,我们可以直接推广到很多类似的场合。例如,用户请求服务器资源的排队问题、早上上班族搭乘公交车/地铁的班次配置问题等等,这些问题都可以使用这个模型来进行求解。



