我最近一个教程《利用python做逻辑回归》,其中里面需要学习的知识点有通过优化算法可以加速机器学习的拟合速度,最常用的加速方法是PCA方法,也称为主成分分析,如果你的算法拟合速度很慢,很可能的原因是输入数据的维度过多,通过PCA的方法提速是个很好的想法,同时也是PCA主要用途,另外一个用途是数据可视化。
如何理解PCA可视化的价值:
可以用iris数据做基础数据,通过无PCA与有PCA的数据进行对比;
用PCA加速逻辑回归的速度;
1. PCA可视化
一般的在机器学习中,我们可以可视化我们的数据,可视化2、3维的数据没有挑战,但是,Iris的数据有4个维度,我们常用的可视化方法就无法完成任务了,PCA应运而生,可以将4维数据降到2、3维数据,这让我们就可以可视化,并让我们更好的理解数据。Iris 数据是scikit-learn的自带数据,不需要下载,通过下面的代码进行加载。
import pandas as pd
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
# load dataset into Pandas DataFrame
df = pd.read_csv(url, names=['sepal length','sepal width','petal length','petal width','target'])
数据示例:

1.1 标准化数据
在利用PCA之前,需要对特征进行处理,通过 StandardScaler 来标准化数据特征,平均值0,标准差为1的数据。这个是机器学习的通用做法,如果想知道非标准化数据的影响,可以参考这文章。
from sklearn.preprocessing import StandardScaler
features = ['sepal length', 'sepal width', 'petal length', 'petal width']
# 分离特征
x = df.loc[:, features].values
# 分离响应变量
y = df.loc[:,['target']].values
# 标准化
x = StandardScaler().fit_transform(x)
转化过程:

1.2 PCA降维
原始数据有4维分别为:sepal length, sepal width, petal length, and petal width,在本节,PCA将把原始数据4维变成2维, 我应该注意,降维后,通常没有为每个主要组件分配特定的含义。新组件只是变化的两个主要方面
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
principalComponents = pca.fit_transform(x)
principalDf = pd.DataFrame(data = principalComponents
, columns = ['principal component 1', 'principal component 2'])
将为过程:

1.3 PCA并保留2个主要的维度
finalDf = pd.concat([principalDf, df[['target']]], axis = 1)
合并数据,finalDf 是最后的数据。
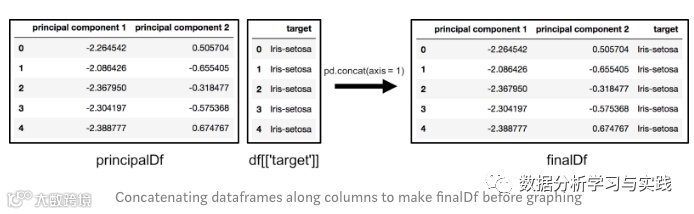
1.4 可视化2维数据
本节仅绘制二维数据。请注意,在下图中,各类之间似乎相互分离良好。
fig = plt.figure(figsize = (8,8))
ax = fig.add_subplot(1,1,1)
ax.set_xlabel('Principal Component 1', fontsize = 15)
ax.set_ylabel('Principal Component 2', fontsize = 15)
ax.set_title('2 component PCA', fontsize = 20)
targets = ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica']
colors = ['r', 'g', 'b']
for target, color in zip(targets,colors):
indicesToKeep = finalDf['target'] == target
ax.scatter(finalDf.loc[indicesToKeep, 'principal component 1']
, finalDf.loc[indicesToKeep, 'principal component 2']
, c = color
, s = 50)
ax.legend(targets)
ax.grid()
示例:

1.5解释变化
解释的变化告诉您可以将多少信息(方差)归因于每个主要成分,这很重要,因为虽然您可以将4维空间转换为2维空间,但是这样做会丢失一些数据(信息),使用 explainedvarianceratio_,您会看到第一个主成分包含72.77%的变化,第二个主成分包含23.03%的变化。这两个部分加在一起包含95.80%的信息
pca.explained_variance_ratio_


