
几周前,我发现了一个快乐的现象,那就是[[Linked List-1]], 和[[堆栈]], [[队列]] 抽象的数据类型,我们可以通过使用它们来建立! 一旦我意识到这些简单的数据结构实际上是在我每天的工作和生活中使用的许多东西的表面之下,我就有点被吓坏了。但是,事实证明,这只是数据结构的冰山一角!为什么呢?因为,当然是这样的。这毕竟是计算机科学,问题可以通过许多不同的方式来解决!数据也是如此,它可以通过不同的方式来解决。而数据也是如此,它可以用不同的方式来组织。
到目前为止,我们主要只处理了一种数据结构。但今天,我们将变得有点疯狂,并将我们的数据打乱顺序!这是因为我们终于要深入研究非线性数据结构了。这是因为我们终于要深入研究非线性数据结构了,从我个人最喜欢的树开始!"。
种植你想要的任何种类的分支!
你可能还记得,有很多不同的方法来对数据结构进行分类。对于我们如何存储数据,其中一个更广泛的分类是我们的数据是否是_线性的--也就是说,我们的数据是否有一个序列和一个顺序来构建和遍历。在线性数据结构如数组或链接列表--数据是有顺序的,而且这个顺序很重要;你遍历线性数据结构的方式与它的顺序直接相关,因为线性数据结构中的元素只能按顺序被遍历。
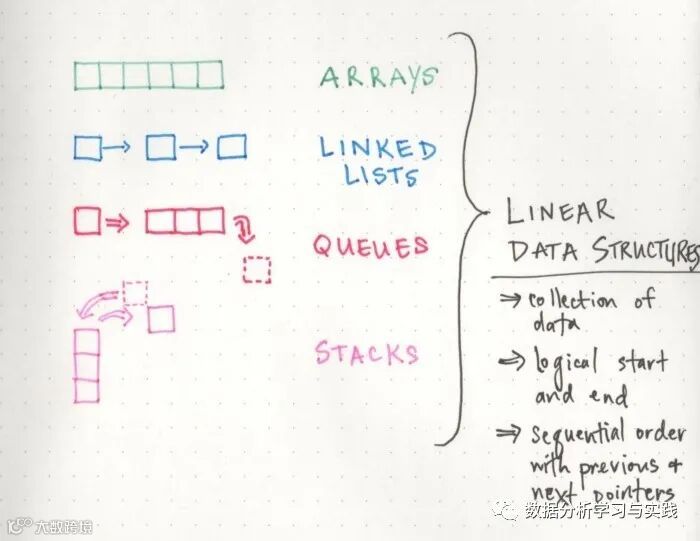
野外的线性数据结构
但正如我们现在所知道的,还有非线性数据结构! 我读的越多,了解的越多,它们看起来就越酷。但是,它们也可能有点棘手和不方便,这就是为什么首先对线性数据结构有一个很好的掌握是非常有帮助的,这样我们就能从一开始就理解它们之间的根本区别。
在非线性数据结构中,数据并不真正遵循一个顺序--至少,不是一个明显的数字顺序,就像数组或链接列表那样。因为数据不一定需要按照特定的顺序排列,所以以非顺序的方式遍历非线性数据结构很容易(实际上也很常见)。
非线性数据结构的一个重要类型是树。如果我们想了解树以及如何谈论它们,我们需要能够识别树的各个部分 然而,尽管它们看起来与我们迄今为止所处理的结构非常不同,但它们实际上是由相同的东西组成的。
树--像链表一样--是由节点和链接组成的。
所有的树,不管是橡树、枫树还是银杏,都是以一组坚实的根系开始发芽的。在树形数据结构中,你也总是必须有一个根,即使你没有其他东西。事实上,如果我们只有一个根,我们就只有一个节点。但是,这里就变得有趣了:一个根节点可以与多个其他节点建立链接。这就是我们到目前为止所看到的线性结构与我们现在所学的树之间的根本区别。一个节点可以连接到许多其他节点,这意味着树木可以以不同的形状和方式生长。

识别树形数据结构的各个部分
在谈到树的时候,这里有一些好的术语需要了解。
root:树的最顶端的节点,它从来没有任何链接或边缘与之相连
link/edge:父节点包含的引用,告诉它它的子节点是什么。
Child:任何有一个链接到它的父节点的节点。
Parent:任何有对另一个节点的引用或_链接的节点
Sibling:任何一组节点都是同一个节点的孩子。
Internal:任何有一个子节点的节点(基本上是所有的父节点)。
Leaf:树中没有子节点的任何节点
如果这些术语让人感觉难以承受,我发现把树状数据结构想成是家庭树,甚至是公司的阶梯,是很有帮助的。数据总是分层的。你会有一个人(根节点)在顶部,他委托给其他一些节点(父母节点),这些节点可能有也可能有其他人向他们报告(子节点)。或者你有一个庞大的家族,有父节点、子节点,所有的节点都通向一个祖先的根节点。
只要你能记住数据的本质是分层的,那么这些行话就应该可以让你不那么担心地去思考。
树的真相
不管一棵树长什么样,有多少树枝或树叶,或者它长得多大,有一些普遍的 "树的真理 "是不言而喻的。
我发现,当我们把它们形象化时,这些东西就更容易理解了,所以我们在这里要靠一些例子。让我们看一下下面这棵树。它总共有10个节点,包括根节点。

树的真相:一棵树的链接总是比它的节点总数少一个
这棵树的有趣真相是,它有10个节点,但有9条链接或边。这里有一种关系,无论节点数多少都是真实的,而且有一个简单的经验法则我们可以记住。
如果一棵树有n个节点,它的边数总是少一个(n-1)。
如果我们看一下这棵树,就会开始明白这是为什么。根节点是一个永远不可能有任何父节点的节点。因此,它永远不可能有任何东西来引用它。如果每个节点都必须有一个其他节点通过链接/边来引用它(除了根节点),那么我们总是可以确定我们的树将有n-1个链接,当n是树中节点的总数。我们不用遍历树就能轻易知道这些信息,这有多酷(和强大!)?
但是,等等--这里还有一个可能更酷的事实:树实际上包含在它们之中的树!这是很重要的。

树的真相:树是递归数据结构
树是递归数据结构,因为一棵树通常是由更小的树--通常被称为子树--在其内部组成。树中一个节点的子节点很可能是另一棵树的父节点(使其成为子树的根节点)。在编写穿越或搜索树的算法时,这可能非常有趣,因为树的嵌套有时会导致我们编写递归搜索算法。
但是我们现在还不会去研究树的遍历。相反,我们会先看看一些更重要的东西:我们可以用不同的方式对树进行分类,这在以后的工作中会很有用。
你的树有多高?
由于树有许多不同的形状和大小,所以能够识别和理解你所处理的是哪种类型的树,以及这些数据是什么样子的,是超级重要的。为此,有两个属性是最重要的,当涉及到你正在处理什么类型的树,以及你的数据在该树中的位置时,需要讨论。
在大多数情况下,我们最关心的两个属性是节点的深度或节点的高度。
思考节点的深度的一个简单方法是回答这个问题。这个节点离树的根部有多远?
但在这种情况下,我们怎么知道什么是 "远"?好吧,尽管我们还没有深入了解树形遍历的所有复杂性,但只有一种方法可以遍历或搜索一棵树:通过建立一条路径并沿着根节点向下的边/链接。因此,我们可以通过计算从根节点到达该节点所需的链接数来确定一个节点离根节点有多远。
在这里的例子中,粉色节点的深度是2,因为正好有2条链接连接根节点和粉色节点。然而,紫色节点的深度是3,因为从根节点到紫色节点需要3个链接。

树形数据结构上的节点的深度和高度
现在我们知道了深度的作用,第二个属性就比较容易了。一个节点的高度可以通过问问题来简化。这个节点离它最远的叶子有多远?(记住:我们在计算机的野生世界里把树颠倒过来,这就是高度以这种方式确定的原因!)。
因此,我们可以通过找到一个节点最远的子叶,并计算到达它所需的链接路径来找到它的高度。在这个例子中,橙色节点的高度是3,因为它最远的子叶(实际上有三个!)离橙色节点有三个链接。如果你能弄清楚橙色节点的深度是多少,就可以得到奖励分
高度属性最酷的地方在于,根节点的高度自动就是整个树本身的高度。基本上,这意味着一旦我们找到了离根节点最远的叶子节点,我们现在就知道了树中最长的可能路径,这就告诉了我们它实际上有多高!"。
深度和高度之所以如此重要,是因为它们告诉我们很多关于树的样子,一目了然。而关于树的问题(我相信现在大家都知道)是,它们都可以看起来不一样。这方面的一个简单例子是平衡的树与不平衡的树。

平衡的树与不平衡的树
如果任何两棵兄弟姐妹子树的高度相差不超过一个级别,那么这棵树就被认为是平衡的。然而,如果两棵兄弟姐妹子树在高度上有明显的差异(并且有超过一级的深度差异),那么这棵树就是不平衡的。
当我们谈论树的操作,特别是遍历时,就会出现平衡树。这背后的想法是,如果我们能够遍历一棵树并减少一半的操作,我们就会有一个性能更好的数据结构。然而,在一棵不平衡的树上,情况肯定不是这样的,因为一个子树可能比它的兄弟姐妹的子树大得多。平衡树所解决的很多操作效率问题实际上被称为二叉树--但下周会有更多的内容!
挖掘树的根
为了真正地欣赏树的力量,我们必须在其应用的背景下看待它们。换句话说:除非你在野外看到它们,否则它们可能并不那么酷。
一个简单的例子是在面向对象的语言中:主 "对象 "是根节点,而从它继承的类是主类的子女。当你想一想,这就更有意义了;事实上,它经常被称为 "类的层次结构",很好地解释了层次树数据结构。

想想看,我们都在树荫下晒了这么久,却不知道。
资源
如果你是一个树木拥抱者,或者是一个树木爱好者,或者只是想了解更多一点,请查看这些有用的链接!
Data Structures: Introduction to Trees, mycodeschool
Data Structures: Trees, HackerRank
Trees, Professor Jonathan Cohen
Tree Data Structures, Professor David Schmidt
Balancing Trees, Professor R. Clayton


