泊松分布-泊松过程-指数分布-gamma分布

了解泊松过程并使用Python模拟泊松过程

让我们看看泊松序列是什么样子的。

上图描述了一家医院急诊室的病人到达时间。可以看出横轴是病人累积数量，纵轴是病人的到达时间时间，单位为小时（从任意时间点开始计时）

从斜率可知， 平均到达率是每小时5个病人。

事实证明，这种"到达"数量可以用泊松过程非常好地描述。

泊松过程在各行各业都可以看到，举一些身边的例子：

• 在药店，在某个时间间隔内到送药窗口的病人数量
• KFC在周日中午12点到下午4点出售的每小时热狗数量。
• 一家医院的超声波机的故障次数。
• 平日上午8点到11点，通过某个十字路口的车辆数量。
• 暴露在一束光子下的光电探测器在1分钟内产生的电脉冲的数量。

那如何利用泊松分布来解决问题呢，让我们开始进入泊松过程的奇妙世界!

1.  了解随机变量和随机过程

随机变量中的"变量"一词是个容易让人误解的说法。一个随机变量，通常用 等表示，本质上是一个函数，和所有常见函数一样，X 对应一个定义域和一个范围。

1.1 Domain( X )：定义域

X的定义域是随机结果的样本空间。这些结果是在进行某种随机实验时产生的，比如抛出2枚硬币。这些结果不一定数字。例如，(徽, 徽)或(花, 徽)是掷硬币实验的两种可能结果。

1.2 Range( X )：值域

X的值域是实数的集合。

随机变量 将事件的样本空间映射到一个值域。

为什么 X 被称为一个随机变量？这是因为 X 用一个概率分布从range( X )中输出一个值，这个概率分布应该代表样本空间中的事件发生的可能性。在上图中，这个概率分布可以是:

{1 → 0.2, 2 → 0.45, 3 → 0.15, 4 → 0.2}

请注意，所有结果的概率之和为1。

X的PMF图

X可以是 离散的 或 连续的 。

• 一个离散的随机变量的范围是可数的无限的，例如整数的集合。离散 X 的一个现实例子是在某个时间间隔内通过一个十字路口的汽车数量。离散随机变量的概率分布被称为Probability Mass Function（PMF）。

• 一个连续的随机变量的范围是实数的集合，即一个不可计数的无限集合。纯粹连续的 X 的现实世界的例子并不容易找到。一个近似的例子是某地一年中某一特定时间的温度，测量的精度可以达到某个任意小的精度。连续随机变量的概率分布被称为Probability Density Function(PDF）。

现在我们来看看什么是随机过程:

2. 随机过程

一个的随机过程是一个随机变量的序列，X1, X2, X3,...等 通常以时间为索引。每个变量都可以从某种概率分布中获得不同的值。请看下面的随机过程的图示。

一个随机过程

一个随机过程可以是离散的，也可以是连续的，这取决于其中变量 X1, X2, X3 等是离散变量还是连续变量。

我们现在准备看看泊松过程是一种什么样的过程。

3. 泊松过程

泊松过程可以用来模拟事件发生的数量，如到达急诊室的病人数量，在一定的时间内，如24小时，假设人们知道这些事件在一定时间内的平均发生率。

泊松过程具有以下特性：

1. 它是由一连串的随机变量 X1, X2, X3, ...Xk 组成的，每个变量代表某个事件的发生次数，例如，在某个时间段内病人走进急诊室的数量。
2. 它是一个随机过程。每次你运行泊松过程，它都会按照我们即将看到的某种概率分布产生不同的随机结果序列。
3. 一个离散过程:泊松过程的结果是某个事件在指定时间段内发生的次数，这无疑是一个整数，即一个离散的数字。
4. 它有独立的变量。意思就是该过程预测在任何给定区间内发生的事件的数量与任何其他不相干的区间内的数量无关。例如，
• 从0点（观察开始）到上午10点，走进急诊室的人数
• 从下午3点33分到晚上8点26分
• 从晚上11点到晚上11点05分等的人数无关
5. 泊松过程的组成变量 X1，X2，X3，...Xk 都具有相同的分布。
6. 泊松过程的组成变量 X1，X2，X3，...Xk 都具有泊松分布

在单位时间内发生 个事件的概率，给定单位时间的平均发生率为 。

上述公式给我们提供了在单位时间内发生 事件的概率，给定的平均发生率为λ事件/每单位时间。

以下4张图显示了不同的λ值下PMF的形状：

＝0.1、1.0、5和20个事件的

在每张图中，你可以看到概率在相应的λ值处达到峰值，并且在这个值的两边逐渐变小。

在每张图中，所有可能的 值的概率之和总是1，也就是说，其中结果必然实现一个。

让我们仔细看看λ =5时的情况。在我们的例子中，这相当于每小时有5个病人到达。一小时内有0，1，2，3，...，10，11，...等病人走进急诊室的概率是这样的。

鉴于每小时平均有5名病人走进急诊室，一小时内有 名病人到达的概率。

正如你所看到的，概率在 时达到峰值。

为了知道 病人在 小时内走进急诊室的可能性，我们将其建模为具有速率（ ）的泊松过程。在时间 中发生 次的PMF的相应公式是如下:

在单位时间内λ到达的情况下， 时间内 到达的概率。

以下一组概率分布都是利用上述泊松分布公式，通过不同的时间间隔 对速率 进行缩放产生的。

考虑到λ=每小时5人，在时间t内有 人到达的概率.

4. 对到达间时间进行建模

泊松过程有一个显著的子结构。尽管事件发生的数量是用离散泊松分布来建模的，但连续事件之间的时间间隔可以用指数分布来建模，指数分布是连续分布。

让我们进一步探讨这个问题。

让 等 是随机变量，这样。

• X1 = 过程开始与第一个事件之间的时间间隔，即第一个 到达 的时间
• X2 = 第一个和第二个到达之间的间隔时间。
• X3= 第二次和第三次到达之间的间隔时间。
• 以此类推。

代表第 次和第 次到达之间的间隔时间的随机变量 的分布是:

间隔时间是指数分布的

随机变量 的PDF如下:

泊松过程中到达时间的PDF值

他的CDF如下：

泊松过程中的到达时间的CDF

请记住，X 的CDF返回连续到达的时间间隔小于或等于某个值 t 的概率。

5. 模拟泊松过程中的到达间隔时间

我们现在有足够的信息来生成泊松过程中的到达间隔时间。我们通过使用逆向变换取样技术来做到这一点，在该技术中，我们构建了CDF的反函数，并从 Uniform(0,1)分布中输入不同的概率值。这样我们就可以得到相应的概率的到达时间。

抵达间隔时间的CDF的反函数是：

抵达间隔时间的CDF的倒数

如前所述，我们把来自连续均匀分布 Uniform(0,1)的概率值输入这个函数。我们很快就会看到如何使用几行Python代码以编程方式完成这一操作。

现在，以下是前10名病人在急诊室的到达时间（以小时为单位）的表格。我们使用上述公式生成了这个日期，λ设置为每小时5个病人。

每小时到达人数

这里是前500个到达的间隔时间图。正如预期的那样，它是CDF图的倒数:

区间到达时间的CDF的倒数

6. 在泊松过程中对到达时间进行建模

现在我们知道了如何产生到达间歇时间，就很容易产生病人的到达时间。

从上面显示的10个样本到达时间的表格中，我们可以推导出以下内容。

第一个病人的到达时间 = x1 = 0.431257556

第二个病人的到达时间 =  x1 = 0.4312576。 x1第一个和第二个病人之间的到达时间 =
x1 + x2 = 0.431257556 + 0.264141966 = 0.6954

第三位病人的到达时间=
x1 + x2 + x3 = 0.431257556 + 0.264141966 + 0.190045932 = 0.885445

...以此类推

考虑到X1, X2, X3,...Xk 是到达时间的间隔，如果我们定义 T1, T2, T3, ...Tk为代表病人到达急诊室的时间的变量，我们看到。

T1 = X1
T2 = X1 + X2
T3 = X1 + X2 + X3
...
Tk = X1 + X2 + X3 + ... + Xk

请注意，由于T1, T2, T3...Tk被定义为随机变量的线性组合X1, X2, X3,...Xk，所以变量T1, T2, T3,...Tk也是随机变量。

这里还有一个非常有趣的事实。

由于T1, T2, T3...Tk 各自是指数分布的随机变量 X1, X2, X3,...Xk 的总和，所以随机变量T1, T2, T3,..., Tk遵循伽马分布。

泊松过程中的到达时间遵循伽马分布，这是一个连续分布。

让我们退一步，注意到我们是如何顺利地从一个离散分布到一组连续分布的！这就是泊松过程的神奇结构。虽然过程本身是离散的，但其子结构完全由连续随机变量表示。

下面的示意图总结了构成泊松过程的三个主要分布:

泊松过程的子结构

7. 模拟泊松过程

我们现在准备模拟整个泊松过程。

要做到这一点，我们需要遵循这个简单的2步程序。

1. 对于给定的平均发病率λ，使用反CDF技术来产生到达时间间隔。
2. 通过构建区间到达时间的运行总和来生成实际到达时间。

下面是模拟泊松过程的Python代码。

import randomimport math
_lambda = 5_num_arrivals = 100_arrival_time = 0
print('RAND,INTER_ARRV_T,ARRV_T')
for i in range(_num_arrivals):	#Get the next probability value from Uniform(0,1)	p = random.random()
	#Plug it into the inverse of the CDF of Exponential(_lamnbda)	_inter_arrival_time = -math.log(1.0 - p)/_lambda
	#Add the inter-arrival time to the running sum	_arrival_time = _arrival_time + _inter_arrival_time
	#print it all out	print(str(p)+','+str(_inter_arrival_time)+','+str(_arrival_time))```
模拟泊松过程的Python代码
这里是这个程序的输出，给我们一个完全模拟但100%真实的泊松序列。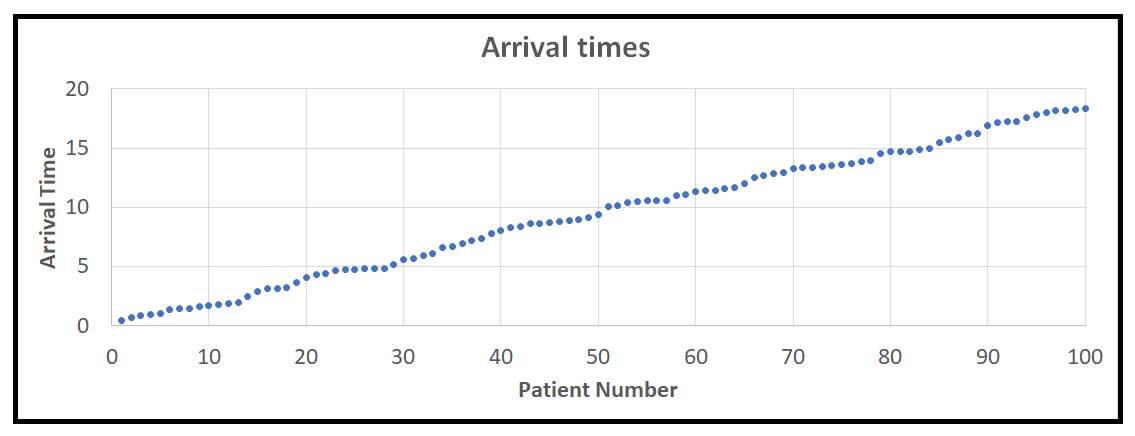
![](https://pic-1309577484.cos.ap-beijing.myqcloud.com/img/1_4JEiRCM7sm6k1g1XK_sQbg.png)

泊松式模拟到达量
如果将到达时间四舍五入到最接近的小时，并将图表旋转90度，就可以发现每小时平均到达率为5。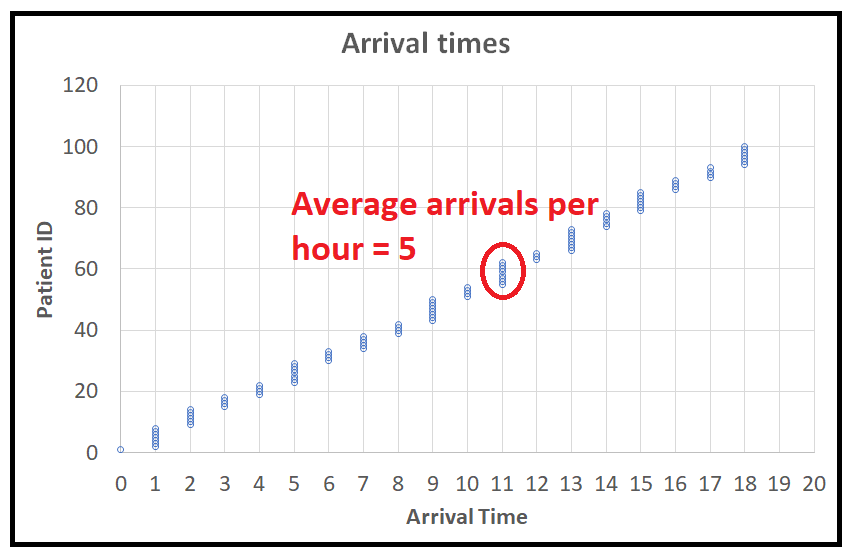
![](https://pic-1309577484.cos.ap-beijing.myqcloud.com/img/1_eYB-Ai2zNLo9TdshTtS6Hw.png)
这里是生成的完整源代码:
```pythonimport randomimport mathimport statisticsimport matplotlib.pyplot as plt

_lambda = 5_num_events = 100_event_num = []_inter_event_times = []_event_times = []_event_time = 0
print('EVENT_NUM,INTER_EVENT_T,EVENT_T')
for i in range(_num_events):	_event_num.append(i)	#Get a random probability value from the uniform distribution's PDF	n = random.random()
	#Generate the inter-event time from the exponential distribution's CDF using the Inverse-CDF technique	_inter_event_time = -math.log(1.0 - n) / _lambda	_inter_event_times.append(_inter_event_time)
	#Add the inter-event time to the running sum to get the next absolute event time	_event_time = _event_time + _inter_event_time	_event_times.append(_event_time)
	#print it all out	print(str(i) +',' + str(_inter_event_time) + ',' + str(_event_time))
#plot the inter-event timesfig = plt.figure()fig.suptitle('Times between consecutive events in a simulated Poisson process')plot, = plt.plot(_event_num, _inter_event_times, 'bo-', label='Inter-event time')plt.legend(handles=[plot])plt.xlabel('Index of event')plt.ylabel('Time')plt.show()

#plot the absolute event timesfig = plt.figure()fig.suptitle('Absolute times of consecutive events in a simulated Poisson process')plot, = plt.plot(_event_num, _event_times, 'bo-', label='Absolute time of event')plt.legend(handles=[plot])plt.xlabel('Index of event')plt.ylabel('Time')plt.show()
_interval_nums = []_num_events_in_interval = []_interval_num = 1_num_events = 0
print('INTERVAL_NUM,NUM_EVENTS')
for i in range(len(_event_times)):	_event_time = _event_times[i]	if _event_time <= _interval_num:		_num_events += 1	else:		_interval_nums.append(_interval_num)		_num_events_in_interval.append(_num_events)
		print(str(_interval_num) +',' + str(_num_events))
		_interval_num += 1
		_num_events = 1
#print the mean number of events per unit timeprint(statistics.mean(_num_events_in_interval))
#plot the number of events in consecutive intervalsfig = plt.figure()fig.suptitle('Number of events occurring in consecutive intervals in a simulated Poisson process')plt.bar(_interval_nums, _num_events_in_interval)plt.xlabel('Index of interval')plt.ylabel('Number of events')plt.show()

• 模拟泊松过程中连续事件之间的时间。
• 模拟泊松过程中连续事件的绝对时间。
• 在模拟泊松过程中连续发生的事件的数量。
• 计算每单位时间的平均事件数。

如果你喜欢这篇文章，请在关注我，关于回归、时间序列分析和预测等主题的提示、方法和编程。