(第二弹)python实现股票价格布朗运动的正态性检验与蒙特卡洛模拟的拟合优度分析
前情回顾:一周前,我们复习了经典期权定价理论中关于股票价格服从几何布朗运动的部分,并用python实现了股票价格布朗运动的蒙特卡洛模拟方法,接下来让我们用一些科学的统计方法检验我们得出的结论。

热身准备
#输入外包import numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport scipy.stats as statsfrom scipy.stats import kstest #用于正态性检验import statsmodels.api as smfrom statsmodels.formula.api import ols #用于OLS回归#读取csv,提取股票价格date=pd.read_csv(r'C:\Users\59298\Desktop\homework\000681.csv',sep='\t',encoding='utf-16')pture=pd.DataFrame(date)pture=pture.iloc[:,1]#计算样本数量、mu、sigmadays=len(pture)dt=1#时间间隔为1天
真实股票价格的正态性检验
#计算日收益率、mu、sigmasture=pd.DataFrame(np.zeros((days)))for i in range(days):sture.iloc[i]=pture.iloc[i]/pture.iloc[i-1]-1mu=np.mean(sture)sigma=np.std(sture)#真实数值的正态性检验dsture=sture-sture.shift() #shift()实现sture的列向下平移,即每个单元格滞后一期;ds=s-s(-1)ds_div_s=dsture.div(sture,axis=0)ds_div_s.iloc[0]=0print(kstest(ds_div_s,'norm'))
输出结果:(第一项数值为统计数,第二项为p值)

基本上p值>0.05,均可认为股票服从对应的正态分布。
蒙特卡洛模拟拟合优度分析
#创建股票价格模拟值dataframe,使期初价格与真实值相等num=30 #模拟次数为30psimu=pd.DataFrame(np.zeros((days,num)))psimu.loc[0]=pture.loc[0]#蒙特卡洛模拟for j in range(num):for i in range(days-1):psimu.iat[i+1,j]=psimu.iat[i,j]+psimu.iat[i,j]*(mu*dt+np.random.standard_normal()*sigma*np.sqrt(dt))#股票价格保留两位小数formater='{0:.02f}'.formatpsimu=psimu.applymap(formater)psimu=pd.DataFrame(psimu,dtype='float')
(2)拟合优度分析
#创建各解释变量(平均值mean、极差range、中位数median、方差var、偏度skew、峰度kurt)的dataframepmean=pd.DataFrame(np.zeros((num,1)))prange=pd.DataFrame(np.zeros((num,1)))pvar=pd.DataFrame(np.zeros((num,1)))pskew=pd.DataFrame(np.zeros((num,1)))pkurt=pd.DataFrame(np.zeros((num,1)))for i in range(num):pmean.iloc[i]=psimu.iloc[:,i].mean()prange.iloc[i]=psimu.iloc[:,i].max()-psimu.iloc[:,i].min()pvar.iloc[i]=psimu.iloc[:,i].var()pskew.iloc[i]=psimu.iloc[:,i].skew()pkurt.iloc[i]=psimu.iloc[:,i].kurt()G.iloc[i]=g.iloc[:,i].sum()pmodel=pd.concat([G,pmean,prange,pvar,pskew,pkurt],axis=1)!
#多元线性回归pmodel.columns = ['G','pmean','prange','pvar','pskew','pkurt']#设置被解释变量与解释变量x_var=pmodel.iloc[:,1:6]y_var=pmodel.iloc[:,0]#ols回归,解释变量:pmean+prange+pvar+pskew+pkurtlm_m=ols('G~pmean+prange+pvar+pskew+pkurt',data=pmodel).fit()print(lm_m.summary()) #R^2相当大,而多个解释变量的p值大于0.1,有理由认为存在多重共线性print(x_var.corr()) #初步判断出pvar与prange存在高度共线性
输出结果:
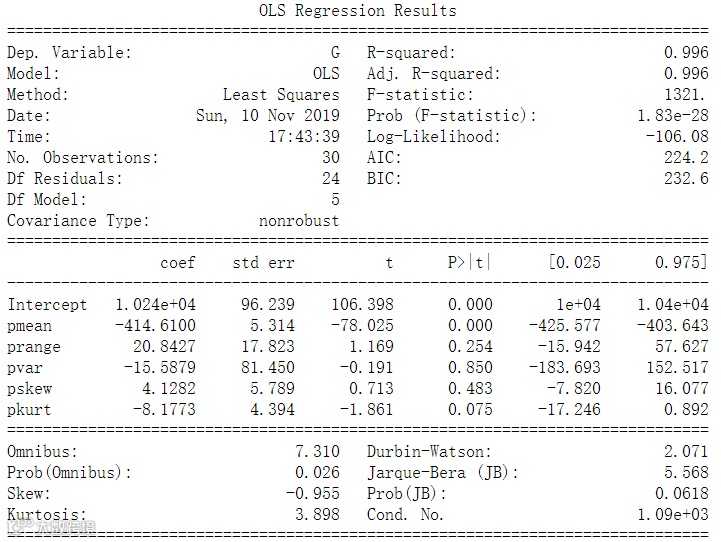

#计算单独解释变量间线性相关系数print('use pearson ,parametric tests pvar and prange')r,p=stats.pearsonr(pvar,prange)print('pearson r**2:',r**2)print('pearson p:',p) #p值很小,认为两者存在共线性
输出结果:

#ols回归,解释变量:pmean+pvar+pskew+pkurtlm_m=ols('G~pmean+pvar+pskew+pkurt',data=pmodel).fit()print(lm_m.summary()) #D.W=2.4,暂且认为无序列相关性
输出结果;

#残差图plt.scatter(pmean,lm_m.resid,label='pmean')plt.scatter(pvar,lm_m.resid,label='pvar')plt.scatter(pskew,lm_m.resid,label='pskew')plt.scatter(pkurt,lm_m.resid,label='pkurt')plt.legend(loc="upper center")plt.ylabel('resid')
输出结果

#观察残差图,发现并没有存在明显的异方差性
#得出结论:均值、方差的偏误都会显著影响拟合优度G值,而有关正态性检验的拟合程度对拟合优度影响不明显.
#因此当我们能够较好地预测真实股价的均值、极差、波动率时,我们可以用其作为限制,从而提高模拟结果的准确程度.

作者:黄昱
编辑校对:郭通


