老师您好:我是今年要毕业的硕士,我是教育专业的,测量统计方面的基础差,我也是第一次涉猎MPLUS和结构方程模型,在结果呈现方式和结果解读上都不确定正确性,我的提问在您看来可能很幼稚很低级,但这代表了我们众多在教育学领域做量化研究的研究人员的困扰。希望老师在看我的疑问时能够见谅,恳请老师指正,感谢老师百忙之中对我的学术扶贫,感恩的心。
本人主要是看书学习相关内容,但书里很多比较简略,做完之后我无法确保我的过程与结果解读是否正确,其中也存在一些疑问,希望老师帮忙解答。其中用字母代表隐藏了一些变量,首先简略介绍一下研究模型和结果:
研究模型:探究有哪些变量可以预测Y1的结果,影响的路径是怎么样的。基于以往研究发现,建构以下假设模型。

研究结果:

首先,以儿童发展结果(Y1)作为因变量,建立空模型(模型 1),即不纳入任何解释变量。空模型的作用主要用检验数据是否需要进行多水平分析,当ICC<0.059时,为低度组内相关;0.059<ICC<0.138时,为中等组内相关;ICC>0.138时,为高度组内相关。结果显示,该模型的ICC=0.459>0.138,因而适合进行多水平模型的处理。
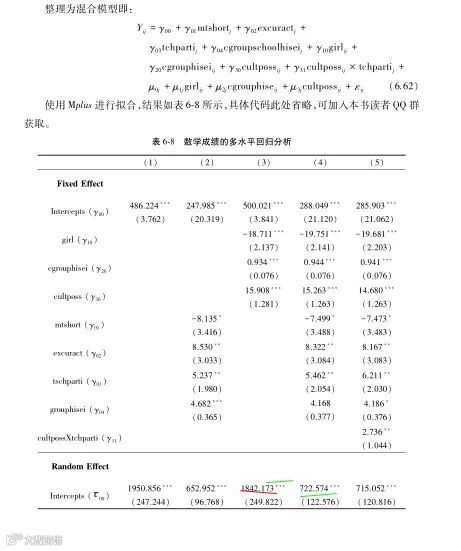
在空模型(模型1)的基础上,仅加入第一层的变量(性别、年龄、入园时长和家庭社会经济地位(SES)等控制变量),以儿童发展结果为因变量,建立模型2,并对“年龄”、“入园时长”和“SES”进行了组均值中心化(groupmean)。由表1可知,“年龄”(b=1.966,p<0.001)、“SES”(b=0.186,p<0.001)对儿童发展结果有显著的正向预测作用。
在模型2的基础上,在第二层加入自变量“X”,以“儿童发展结果”为因变量,建立模型3。结果显示,X对儿童发展结果有极其显著的正向预测作用(b=0.040,p<0.001)。在模型3的基础上,在第二层加入中介变量“m1”、“m2”、“m3”和“m4”,建立全模型(模型4),检验二层中介变量对儿童发展的预测作用。结果显示,“m1”(b=0.041,p<0.05)、“m2”(b=0.324,p<0.01)和“m4”(b=0.622,p<0.05)对儿童发展结果有显著的正向预测作用。
模型5呈现以“X”、“m1”、“m2”和“m3”为自变量,以“m4”因变量,的预测效应。结果显示,“X”对“m4”的直接效应不显著(b=-0.002,p>0.05),“m1”对“m4”的直接效应不显著(b=-0.002,p>0.05),“m2”对“m4”的直接效应不显著(b=-0.023,p>0.05),“m3”对“m4”的直接效应显著(b=0.893,p<0.001)。
模型6、7、8分别呈现以“m1”“m2”和“m3”为因变量,以“X”为自变量的跨层预测效应。“X”对“m1”有显著负向预测作用(b=-0.185,p<0.001),对“m2”(b=0.051,p<0.001)和“m3”(b=0.033,p<0.001)有显著正向预测作用。
为清楚了解影响儿童发展结果的路径,将上述模型中的路径、总效应、直接效应、间接效应的估计值和95%置信区间(95%)单独列于表2。总效应指自变量到因变量的所有效应,包括直接效应和间接效应。直接效应指自变量到因变量的效应,中间不经过第三个变量;间接效应指自变量通过第三个变量对因变量产生的效应。当 95%置信区间不包含 0 时,该效应的估计值显著。

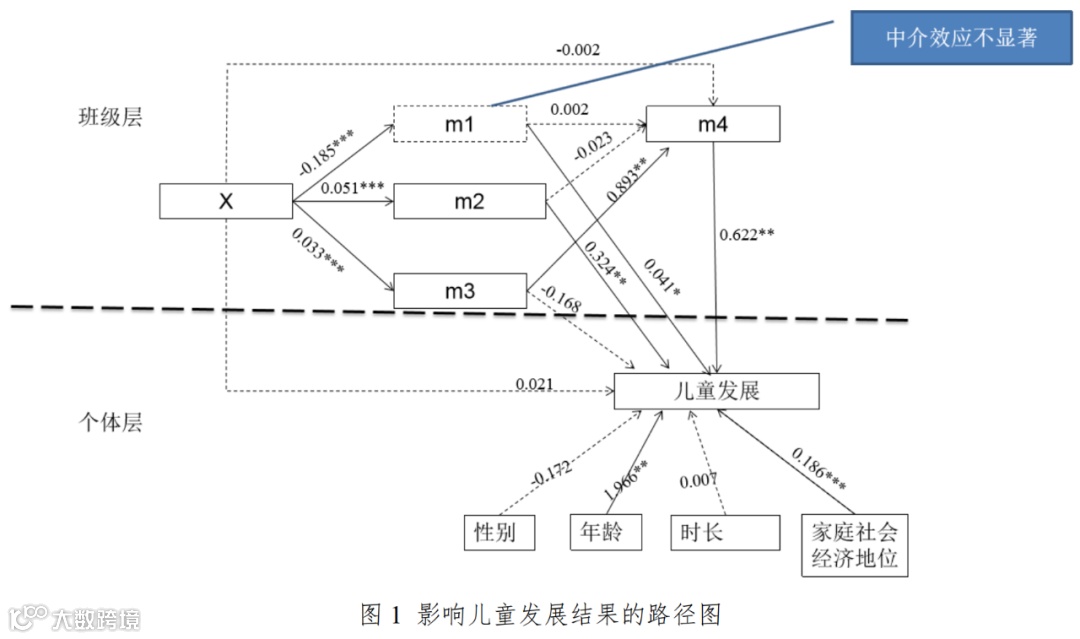
由表2可知,“(X)”—“(M2)”—“(Y)”的间接效应显著,有显著正向预测作用(b=0.017,p<0.05);“(X)”—“(M3)”—“(M4)”—“儿童发展结果(Y)”的间接效应显著,有显著正向预测作用(b=0.018,p<0.05),且为完全中介。总效应显著(b=0.040,p<0.001)和总间接效应显著(b=0.020,p<0.05)。图1直观的展示了影响儿童发展的各因素直接效应及路径。
值得注意的是,“m1”的中介效应不显著,即“X—M1—y”的中介不显著,但是“X—m1”和“m1—Y”的直接效应显著。
1.步骤是否正确,结果呈现方式(即表格)是否正确,结果解读是否正确?
答:建模的步骤没有问题,结果的呈现也符合一般规范,但结果的解读需要注意以下几点问题:
1).多水平模型中中介效应的检验需要采用MCMC置信区间,而不能采用Mplus里给出的置信区间。如果你目前报告的置信区间是Mplus通过“cinterval”调出的置信区间,则需要进行修改和替换并重新检验。一般来说,置信区间分为三种,第一种是基于假设检验的置信区间,参数的理论分布是正态分布,“cinterval”调出的置信区间就是属于第一种,由于乘积参数不服从正态分布,所以涉及到乘积参数的显著性检验则不能看这种置信区间,中介效应就是一种乘积参数检验。第二种是基于非参数Bootstrap的置信区间,这种区间通过对样本数据的重复有放回式自抽样获得,不依赖与参数的理论分布,而是通过自抽样获得参数的经验分布,并根据该经验分布进一步确定参数的置信区间。在单水平中介检验中所查看的置信区间就是这种置信区间。由于目前在多水平情境下还不能进行非参数Bootstrap,所以就用到了下面这种置信区间。第三种是基于参数Bootstrap的置信区间,与非参数Bootstrap的最大区别是:非参数Bootstrap是基于原始数据的抽样,而参数Bootstrap是在各参数分布内直接对参数本身进行抽样,MCMC置信区间就是一种参数Bootstrap置信区间,目前广泛运用于多水平研究中。MCMC置信区间可以通过以下R code实现,也可以在http://quantpsy.org/medmc/medmc.htm输入相关参数估计获得。
require(MASS)a=0.25b=0.31 # replace a and b with estimates drawn from your modelrep=20000conf=95pest=c(a,b)acov <- matrix(c(0.002, -0.005,-0.005, 0.003),2,2) # replace this block with the covariance matrix drawn from your modelmcmc <- mvrnorm(rep,pest,acov,empirical=FALSE)ab <- mcmc[,1]*mcmc[,2]low=(1-conf/100)/2upp=((1-conf/100)/2)+(conf/100)LL=quantile(ab,low)UL=quantile(ab,upp)LL4=format(LL,digits=4)UL4=format(UL,digits=4)hist(ab,breaks='FD',col='skyblue',xlab=paste(conf,'% Confidence Interval ','LL',LL4,' UL',UL4),main='Distribution of Indirect Effect')
2).类似于“由表2可知,(X)—(M2)—(Y)的间接效应显著,有显著正向预测作用(b=0.017,p<0.05)”的表述是不恰当的,首先这是一个中介作用,不是预测作用,其次我们一般也不去界定正向中介或负向中介,中介作用的具体形式可以通过中介路径的系数方向很清晰的看出来。另外,此处应该报告的是中介效应的置信区间,而不是中介效应的点估计和P值。
3).类似于“(X)—(M3)—(M4)—(Y)的间接效应显著,有显著正向预测作用(b=0.018,p<0.05),且为完全中介。”的表述需要注意在具有多重中介甚至存在链式中介的情形下,界定完全中介是没有意义的,因为此时的完全中介并不能说明特定中介变量的中介效应量,实际上,完全中介本身也只是对效应量的粗略说明,应删去完全中介的表述。另外,界定总间接效应的显著性也是没有意义的,原因和以上相同,应删去该类表述。总之,当模型中存在到多个中介时,注意力就需要集中到特定的中介效应上,涉及捆绑多个中介的统计论断则不需要再报告。
4). “m1的中介效应不显著,即X—M1—Y的中介不显著,但“X—m1”和“m1—Y”的直接效应显著”的原因一方面来自于依次检验与乘积系数检验在方法论上的差异,另一方面也可能是由于判断中介效应显著与否的置信区间不是参数BOOTSTRAP下获得的置信区间所致。即便置信区间检验不显著,仍可立论中介效应显著,只要相应的中介路径显著并且在全模型中估计所得。
答:不需要将某个中介变量标成虚框以展示中介不显著,对于结果的路径模型图来说,只需要将不显著的路径用虚线表述即可,至于中介显不显著读者可以在文中进一步检视。

答:你所说的问题是多水平模型中的R-square问题。在多水平模型中没有像传统线性模型中那样的R-square,可以绝对的刻画因变量被自变量解释的方差比例。实际上,一般来说,R-square分为两类,一类是绝对R-square,就是我们通常意义上理解的R-square,另一类是相对R-square,又叫pseudo R-square, 刻画预测变量的加入对模型的相对影响,在多水平模型中使用的就是pseudo R-square。学术界有许多种对于pseudo R-square的界定和算法,而目前使用最广泛的是Snijders and Bosker (1999)提出的pseudo R-square, 即截图中的S&B法,该方法区分组内和组间R-square,具体计算公式如下:

从计算公式可以看出,S&B法下的R-square反映的是加入预测变量后模型减少的方差占总方差变异的比例,视为预测变量的贡献。S&B法具有以下两个特点:1. 无论是计算组内R-square还是组间R-square,均同时考虑不同水平的方差变异;2. 计算组间R-square时依平均的群组规模对组内变异进行折扣,平均群组规模越大,折扣程度越大。需要注意的是,如果数据中群组规模间的差异过大,则需要计算B的调和平均数,而不是算术平均数。这两个特点也是S&B法得到广泛使用的重要原因。
截图中提到的R&B法是Raudenbush and Bryk (2002)提出的一种计算多水平R-square的方法,该方法与S&B法的区别在于,在计算当前水平R-square时不考虑其他层次的变异,比如R&B法下R12的计算公式就是把S&B法下R12中的两个τ02去掉,不难看出,该方法对R-square的计算隔离了组内变异和组间变异。对照这两种方法的计算公式,你就能明白截图中的那些R-square是如何计算出来的。
References:
Raudenbush,S.W., & Bryk, A.S., (2002). Hierarchical linear models: Applications anddata analysis methods. Thousand Oaks, CA: Sage.
Snijders,T.A.B., & Bosker, R.J. (1999). Multilevel analysis: An introduction tobasic and advanced multilevel modeling. London: Sage.
Mplus多水平(跨层次)建模分析
(在线特训营)

课程对象:管理学、心理学、教育学、社会学、政治学、新闻与传播、医学等学科的硕博士或教学科研人员。
课程时间:04.02-04.03
课程形式:线上特训班次
课程费用:2000元(在校学生一律减免200元)
课程名额:为保证小班教学效果,此次课程的学员名额上限为10人,名额优先向硕博士应届毕业生倾斜。


